Natural Convection of Fe3O4-Ethylene Glycol Nano fluid under the Impact of Electric Field in a Porous Enclosure
2018-06-15SheikholeslamiShehzadandKumar
M.Sheikholeslami,S.A.Shehzad,and R.Kumar
1Department of Mechanical Engineering,Babol Noshirvani University of Technology,Babol,Iran
2Department of Mathematics,COMSATS Institute of Information Technology,Sahiwal 57000,Pakistan
3Department of Mathematics,Central University of Himachal Pardesh,Dharamshala,India
Nomenclature

De Diffusion number ρ DensityE,Ex,EyElectric fieldσElectric conductivityFEElectric forceµDynamic viscosity NE Electric field number ε Dielectric permittivity PrE Electric Prandtl number φElectric field potential q Electric charge density Subscripts Ra Rayleigh number s Solid particles Rd Radiation parameter h Hot SE Lorentz force number f Base fluid u,v Horizontal and vertical velocity c Cold x,y Cartesian coordinate nf Nano fluid X,Y Non dimensional coordinate Greek symbols ϕ Volume fraction
1 Introduction
One interesting active method for heat transfer augmentation is Electrohydrodynamic. Raraniet al.[1]reported good correlation for viscosity of nano fluid.Nano fluid has various applications in presence of various external forces.Heat transfer and pressure drop characteristics in the microchannel heat sink(MCHS)have been investigated by Liuet al.[2]They showed that interlaced microchannel leads to better heat transfer performance.Also they proved that pressure drop of the T-Y type microchannel is low.Kumaret al.[3]demonstrated radiative heat transfer of non-Newtonian nano fluid over a Riga sheet.Three-dimensional nano fluid flows was demonstrated by Sheikholeslami and Ellahi.[4]They illustrated that velocity detracts with augment of Lorentz forces. Sheikholeslami and Sadoughi[5]demonstrated water based nano fluid flow in presence of melting surface. Sheikholeslami and Shehzad[6]presented the influence of radiative mode on ferro fluid motion. They were taken into account variable viscosity.Nano fluid concentration has been reported by Hayatet al.[7]in existence of radiative mode.Kumaret al.[8]investigated Joule heating effect on nano fluid flow a rotating system.Sheikholeslami[9]investigated nano fluid EHD flow in a porous media.Sheikholeslamiet al.[10]utilized mesoscopic method for nano fluid forced convection.Promvongeet al.[11]utilized V- finned twisted tapes in a duct to improve the thermal behavior.In fluence of viscous dissipation on heat transfer in a circular micro-channel has been investigated by Liuet al.[12]Sheikholeslami and Seyednezhad[13]simulated nano fluid flow and natural convection in a porous media under the in fluence of electric field.Impact of variable Kelvin forces on ferro fluid motion was reported by Sheikholeslami Kandelousi.[14]Heat flux boundary condition has been utilized by Sheikholeslami and Shehzad[15]to investigate the ferro fluid flow in porous media.Sheikholeslami[16]investigated CuO-water nano fluid flow in a porous enclosure under the impact of Lorentz forces.In recent decade,various researcher published papers about heat transfer.[17−22]
This article intends to model the in fluence of thermal radiation on nano fluid behavior in existence of Coulomb forces via CVFEM.Roles of Darcy number,Rayleigh number,supplied voltage,radiation parameter and Fe3O4volume fraction are presented in outputs.
2 Problem Definition
Figure 1 depicts the porous enclosure and its boundary conditions.Ethylene glycol-Fe3O4nano fluid is utilized.All walls are stationary.In fluence of Darcy and Rayleigh number on contour ofqis demonstrated in Fig.2.Effect ofRaonqis less sensible thanDa.As Darcy number augments the distortion of isoelectric density lines become more.
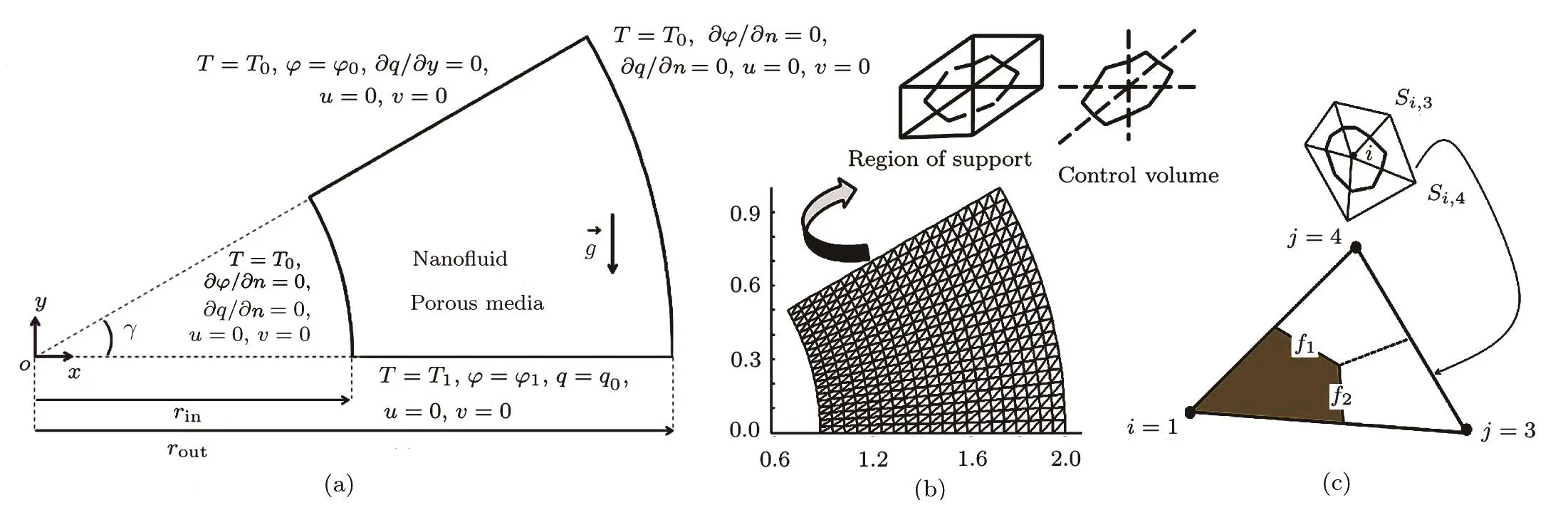
Fig.1 (a)Geometry and the boundary conditions with,(b)Sample mesh,(c)A sample triangular element and its corresponding control volume.

Fig.2 Electric density distribution injected by the bottom electrode when∆φ=6 kV,ϕ=0.005,Rd=0.8.
3 Governing Formula and Modeling
3.1 Governing Formula
The definition of electric field is[23]
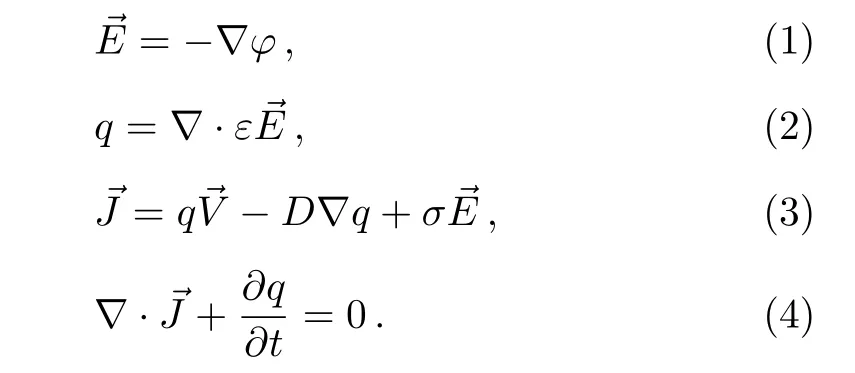
The governing formulae are[20]

Properties of Fe3O4and ethylene glycol are illustrated in Table 1.EFD viscosity is presented by Ref.[1].Table 2 illustrates the coefficient values of this formula.

Table 1 Thermo physical properties of Ethylene glycol and nanoparticles.

Table 2 The physical values of Eq.(13).[1]
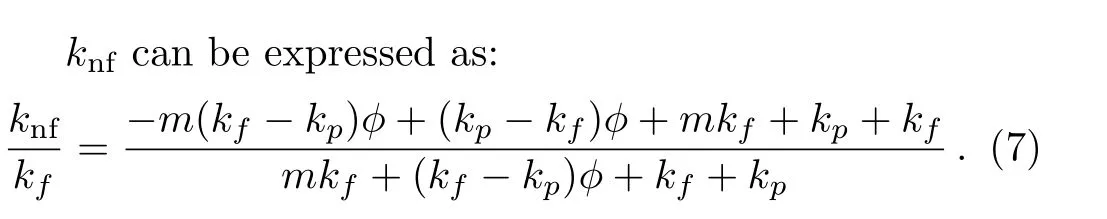
Different values of shape factors for various shapes of nanoparticles are illustrated in Table 3.
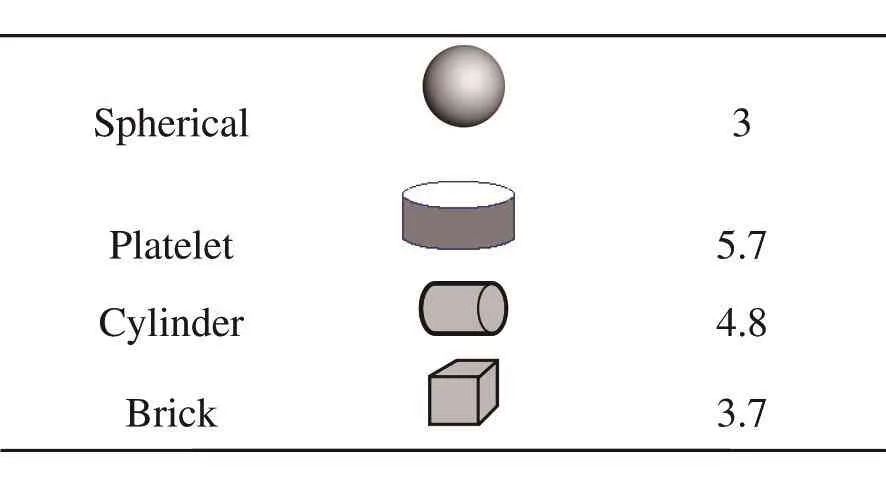
Table 3 The values of shape factor of different shapes of nanoparticles.
So,the final PDE in existence of thermal radiation and electric field in porous media are:[20]Vorticity and stream function should be employed in order to diminish pressure gradient:

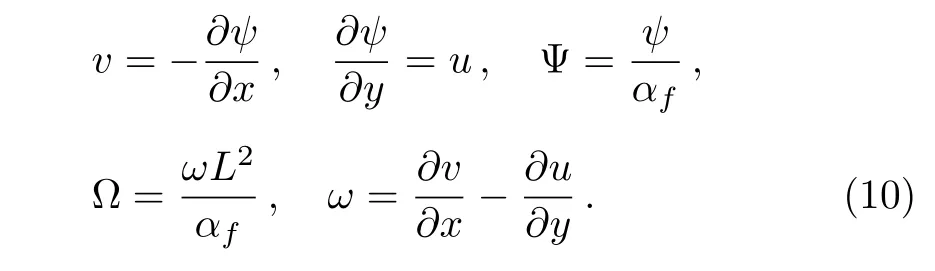
NulocandNavgalong the bottom wall are calculated as:
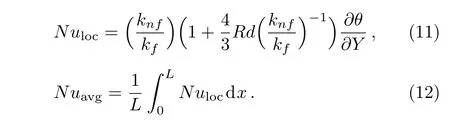
3.2 CVFEM
CVFEM uses both benefits of two common CFD methods.This method uses triangular element(seefig.1(b)).Upwind approach is utilized for advection term.Gauss-Seidel method is applied to find the solution of the algebraic system.Further notes exist in Ref.[24].
4 Mesh Study and Code Validation
Various mesh sizes have been tested to find the mesh independent result.Table 4 demonstrated an example.This table indicated that the size 81×241 of can be selected.The FORTRAN code has been validated by comparing the outputs with those of reported in Ref.[23](seefig.3).Good agreement can be found.

Table 4 Comparison of Nuavealong hot wall for different grid resolution at Rd=0.8,Ra=500,Da=102,∆φ=6,ϕ=0.05,and Pr=6.8.
5 Results and Discussion
In fluence of Coulomb forces on nano fluid natural convection heat transfer is reported considering thermal radiation.Nano fluid viscosity is a function of electric field.The porous enclosure is filled with Fe3O4Ethylene glycol.Roles of Darcy number(Da=10−2to 102),Radiation parameter(Rd=0 to 0.8),supplied voltage(∆φ=0 to 6 kV),volume fraction of Fe3O4(0%to 5%),Rayleigh number(Ra=50 to 500)are depicted.

Fig.3 Comparison of temperature pro file at middle line between the present results and numerical results by Khanafer et al.[23]Gr=104,ϕ=0.1 and Pr=6.8(Cu-water).
In order to find the in fluence of nanoparticles’shape of heat transfer rate,a comparison has been reported in Table 5.As Platelet shape Fe3O4nanoparticle selected,maximum value of Nusselt number can be obtained.In continued result,we used this shape of nanoparticles.Influences of∆φ,Da,andRaon nano fluid treatments are depicted in Figs.4,5,6,and 7.When conduction is dominant,there exist two eddies,which are rotated in opposite direction.In existence of Coulomb forces,thermal plume appears and eddies are stretched.Isotherms become more disturb in presence of electric field.As buoyancy forces augments,another eddy appears.In high values of Rayleigh number,increasing permeability of porous media leads to convert all eddies to one clock wise eddy and thermal plume shift to left side.
Figures 8 and 9 show the impacts of effective parameters on heat transfer rate.The related correlation is:
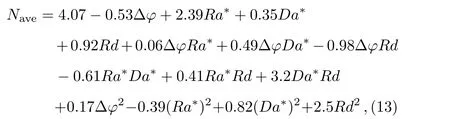
whereRa∗=0.01Ra,Da∗=0.01Da,and ∆φis voltage supply in Kilovolt.Nusselt number augments with increase of Rayleigh number.Electric field helps the convective mode to improve because thermal boundary layer thickness decreases with augment of∆φ.So,Nuaveaugments with augment of∆φ.Temperature gradient near the bottom wall increases with augment of radiation parameter.In fluence of Darcy number is as same as radiation parameter.Therefore,Naveis an increasing function ofRd,Da.

Fig.4 Effect of Darcy number on streamlines and isotherm when Ra=50,∆ϕ=0 kV,ϕ=0.05,Rd=0.8.

Fig.5 Effect of Darcy number on streamlines and isotherm when Ra=50,∆ϕ=6 kV,ϕ=0.05,Rd=0.8.

Fig.6 Effect of Darcy number on streamlines and isotherm when Ra=500,∆ϕ=0 kV,ϕ=0.05,Rd=0.8.
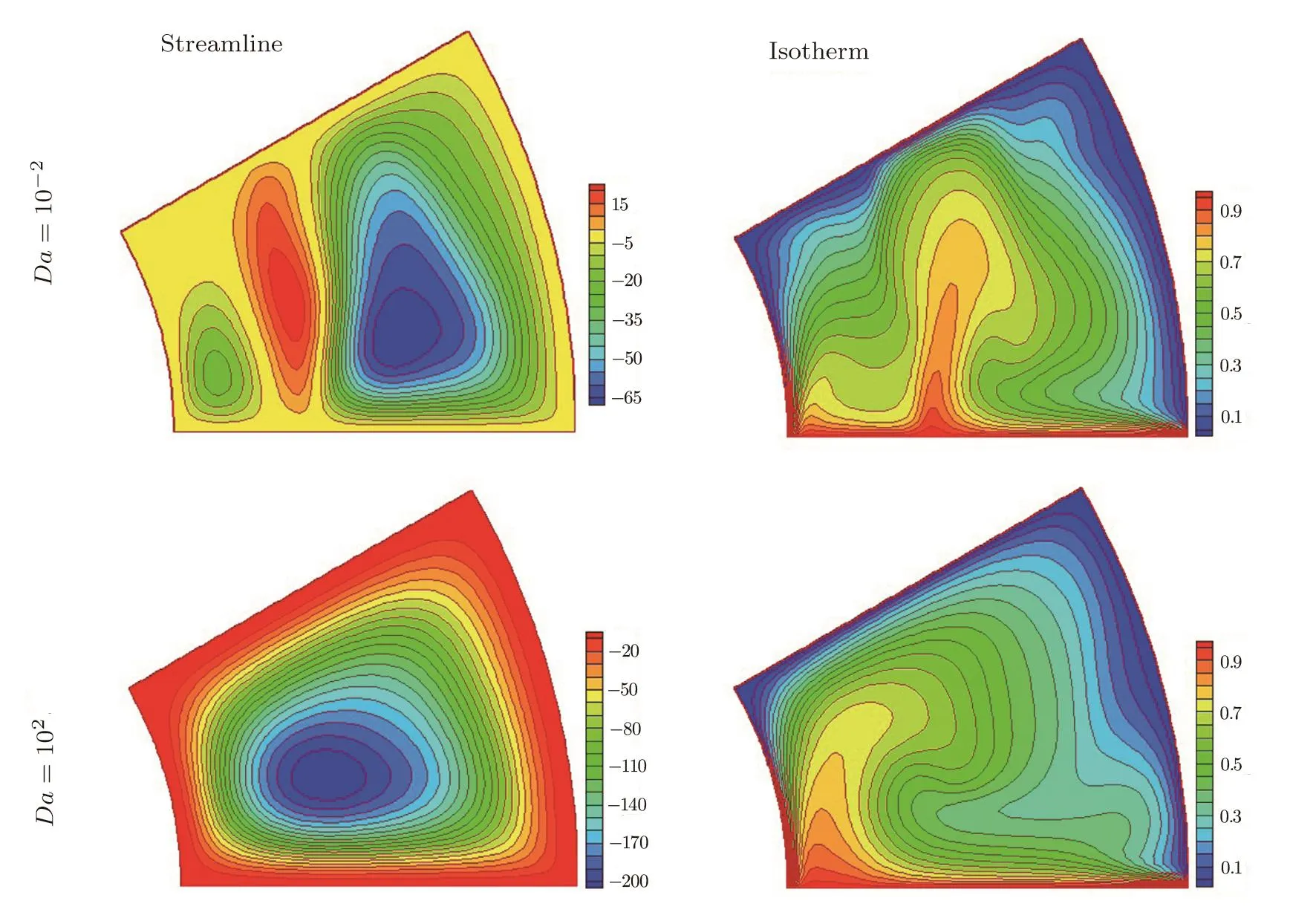
Fig.7 Effect of Darcy number on streamlines and isotherm when Ra=500,∆ϕ=6 kV,ϕ=0.05,Rd=0.8.

Fig.8 Effects of Da,∆φ,Rd,and Ra on average Nusselt number.

Table 5 Effect of shape of nanoparticles on Nusselt number when Rd=0.8,Ra=500,∆φ=6,ϕ=0.05.
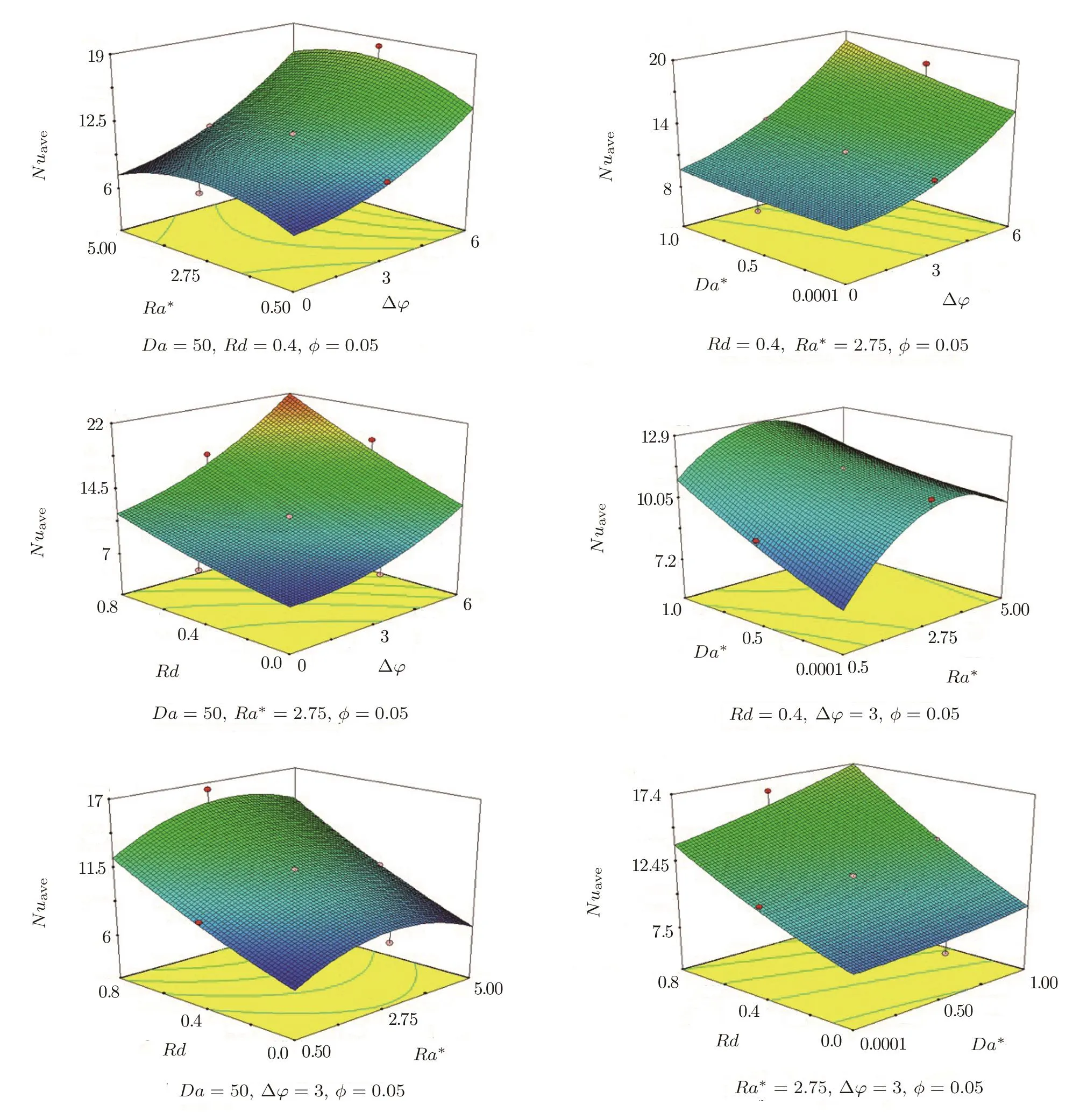
Fig.9 Effects of Da,∆φ,Rd,and Ra on average Nusselt number.
6 Conclusions
Electric field effect on nano fluid natural convection in a porous cavity is simulated by means of CVFEM.Outputs are reported for various values ofRd,Da,∆φ,ϕ,andRa.Outputs demonstrate that the distortion of isotherms becomes more with augment of Darcy number,radiation parameter,and Coulomb forces.As radiation parameter increases,temperature gradient near the hot wall enhances.Nusselt number has direct relationship with Darcy number,radiation parameter and Coulomb forces.
Acknowledgments
We would like to thank theNational Elites Foundationof Iran(http://www.bmn.ir)for their moral and financial support throughout this project.
[1]E.M.Rarani,N.Etesami,and M.N.Esfahany,J.Appl.Phys.112(2012)094903.
[2]H.L.Liu,X.K.An,and C.S.Wang,Int.J.Thermal Sci.120(2017)203.
[3]R.Kumar,S.Sood,S.A.Shehzad,and M.Sheikholeslami,J.Mol.Liq.248(2017)143.
[4]M.Sheikholeslami and R.Ellahi,Int.J.Heat Mass Transf.89(2015)799.
[5]M.Sheikholeslami and M.K.Sadoughi,Int.J.Heat Mass Transf.116(2018)909.
[6]M.Sheikholeslami and S.A.Shehzad,Int.J.Heat Mass Transf.109(2017)82.
[7]T.Hayat,Z.Nisar,H.Yasmin,and A.Alsaedi,J.Mol.Liq.220(2016)448.
[8]R.Kumar,R.Kumar,S.A.Shehzad and M.Sheikholeslami,Int.J.Heat Mass Transf.120(2018)540.
[9]M.Sheikholeslami,J.Mol.Liq.249(2018)1212.
[10]M.Sheikholeslami,T.Hayat,and A.Alsaedi,J.Mol.Liq.249(2018)941.
[11]P.Promvonge,Appl.Therm.Eng.91(2015)298.
[12]H.L.Liu,X.D.Shao,and J.Y.Jia,Int.J.Thermal Sci.66(2013)34.
[13]M.Sheikholeslami and M.Seyednezhad,Int.J.Heat Mass Transf.120(2018)772.
[14]M.S.Kandelousi,Euro.Phys.J.Plus 129(2014)248.
[15]M.Sheikholeslami and S.A.Shehzad,Int.J.Heat Mass Transf.106(2017)1261.
[16]M.Sheikholeslami,J.Mol.Liq.249(2018)921.
[17]M.Sheikholeslami,Int.J.Hyd.Energy 42(2017)19611.
[18]M.Sheikholeslami and H.B.Rokni,Int.J.Heat Mass Transf.118(2018)823.
[19]M.Sheikholeslami,J.Mol.Liq.249(2018)739.
[20]M.Sheikholeslami and A.J.Chamkha,Numer.Heat Transf.Part A 69(2016)781.
[21]M.Sheikholeslami,M.Shamlooei,and R.Moradi,J.Mol.Liq.249(2018)429.
[22]M.Sheikholeslami and S.A.Shehzad,Int.J.Heat Mass Transf.118(2018)182.
[23]K.Khanafer,K.Vafai,and M.Lightstone,Int.J.Heat Mass Transf.446(2003)3639.
[24]M.Sheikholeslami,Application of Control Volume Based Finite Element Method(CVFEM)for Nano fluit Flow and Heat Trasfer,Elsevier(2018),ISBN:9780128141526.
杂志排行
Communications in Theoretical Physics的其它文章
- Thermodynamic Nonequilibrium Features in Binary Diffusion∗
- Ordinary Mode Instability in a Cairns Distributed Electron Plasma
- Thermal Conductivity of Complex Plasmas Using Novel Evan-Gillan Approach
- Spontaneous Emission Originating from Atomic BEC Interacting with a Single-Mode Quantized Field
- Molecular Dynamics Simulations of the Elastic Anisotropy of Pd at Extreme Conditions∗
- In fluences of Crystal-Field and Interlayer Coupling Interactions on Dynamic Phase Diagrams of a Mixed-Spin(3/2,2)Bilayer System∗
