A New Treatment for Some Periodic Schr¨odinger Operators II:The Wave Function
2018-06-15WeiHe贺伟
Wei He(贺伟)
School of Electronic Engineering,Chengdu Technological University,Chengdu 611730,China
1 Introduction
In the previous paper Ref.[1]we study how the Floquet theory manifests in the multiple asymptotic spectral solutions of some periodic Schr¨odinger operators.We have only studied the eigenvalue aspect of these solutions.Following this method,it is very convenient to derive the corresponding asymptotic wave functions,we present the results in this paper.We focus on our canonical examples:the Mathieu equation and the Lame equation,which are the most widely used in periodic spectral problem.Our main conclusion are made for elliptic potentials,but as we have explained,to collect evidences for the proposals a crucial consistent requirement is that the solutions of the Lame equation must reduce to corresponding solutions of the Mathieu equation.Therefore the Mathieu equation,which is much better understood,is included here as a reference example.Unlike in Ref.[1],in this paper we do not use the ellipsoidal wave equation as the example for the elliptic potential as it would lead to lengthly formulae for wave functions,instead the wave functions of Lame equation are already enough for our purpose.
In Sec.2 we derive the wave functions for large energy(weak coupling)perturbation.In Sec.3 we derive the wave functions for small energy(strong coupling)perturbation.Some wave functions have been studied before,we brie fly comment the old materials where earlier treatments can be found.In Sec.4 we explain how the eigenfunctions are related to supersymmetric gauge theory,in the context of Gaueg/Bethe correspondence.[2]
The conclusion of this paper is that the wave functions give further evidence for the relations between multiple asymptotic solutions and the Floquet property associated with multiple periods.Among the wave functions,the eigenfunction(43)is a new solution.
2 Large Energy Wave Function
2.1 The Floquet Wave Function
As we have shown previously,the large energy perturbation can be carried out using a method from KdV theory,[3−4]the wave function is given by

vℓ(x)are given by the KdV Hamiltonian densities.[4]

The dispersion relationλ(ν),whereνis the Floquet exponent,is obtained by the classical Floquet theory,

The relations(3)and(4)give a complete perturbative solution for large energy.
2.2 Mathieu Equation
The potential for the Mathieu equation is
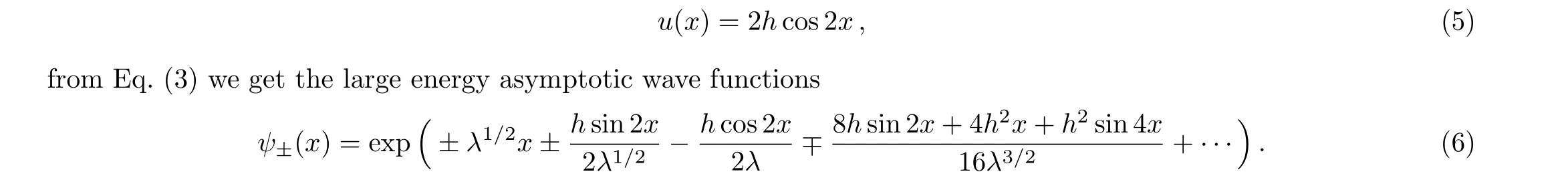
It is clear that withλas the expansion parameter,the coefficients ofλ−ℓ/2are not necessary periodic functions.However,the wave functions must satisfy the Floquet property,this is made clear by the following parameter change using the eigenvalue expansion.
The large energy dispersion relation is a classic result,see for example Refs.[5–8].The relation(4)can be used to compute,it is

Now the coefficients ofν−l,withl>1,are periodic functions,the wave functions take the formψ±(x)=e±iνxϕ(±x)withϕ(x)a periodic function.This wave function is related to theN=2 pure Yang-Mills gauge theory with surface operator,see the discussion in Sec.4.
Another bases of the asymptotic wave functions,commonly used in many literatures,arecem(x)andsem(x).Up to a constant,their relation toψ±(x)is

2.3 Lame Equation
The potential for the Lame equation is an elliptic function,for the large energy perturbation we should use the Weierstrass form to obtain compact formulae.In this paper we use the potential



The corresponding dispersion relation was derived by Langmann,[9]expressed as aq-series,the same expression also appears in the context of its relation to gauge theory,[2]we examined this relation in Ref.[10].Another way to derive the dispersion relation is to use the formula(4),then we get an expression involving quasi-modular functions,[11]
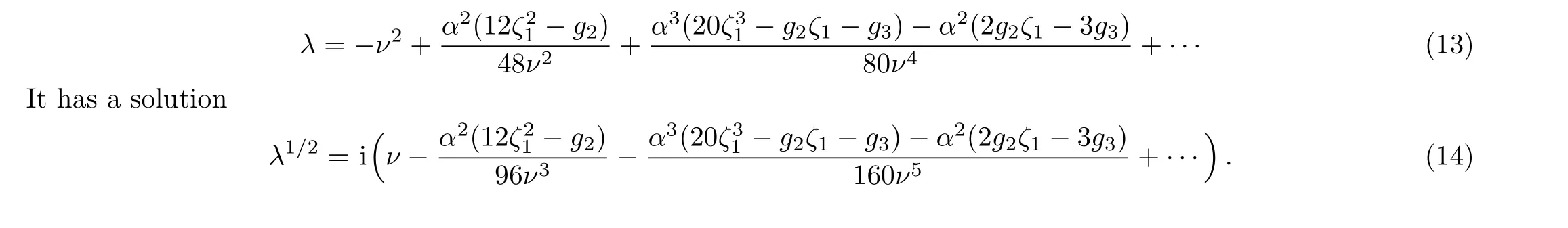
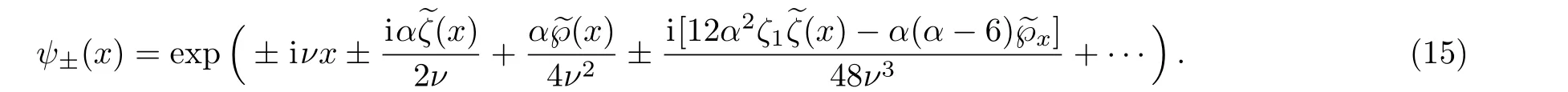
The wave functions also satisfy the propertyψ±(−x)=ψ∓(x).In Sec.4 we would show the connection of this wave function and the partition function of theN=2∗supersymmetric gauge theory with surface operator.
There is a comment about the polynomials of elliptic functions that appear in Eqs.(12)and(15).Recall that any elliptic function can be expressed as a linear combination of zeta functions and their derivatives.In fact,the Hamiltonian densitiesvℓ(x)for the elliptic potential have no pole of order one atx=0,therefore,they are linear combinations of∂kxe℘(x)withk>0.Then the integrated Hamiltonians appearing in Eq.(12)are linear combinations ofxand∂kx˜ζ(x)withk>0.In the wave function(15)the phase e±iνxcontains the linear term ofx,the coefficients ofν−lare linear combinations of∂kx˜ζ(x)withk>0,probably include anx-independent constant term.The constant terms can be absorbed into the normalization constant,then the expressions are linear polynomials of∂kx˜ζ(x)withk>0.Or equivalently,because˜ζ(x)=∂xlnϑ1(πx/2ω1,q),they are linear polynomials of∂kxlnϑ1(πx/2ω1,q)withk>1.This point is important when we connect the wave function to the instanton partition function in Sec.4,especially for higher order terms which we do not explicitly give in Eq.(15).
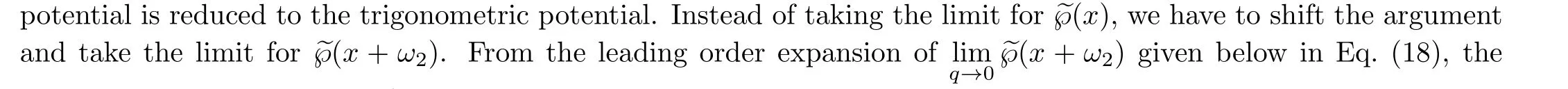
Substituteλ1/2into Eq.(12)we get the wave functions in the Floquet form,

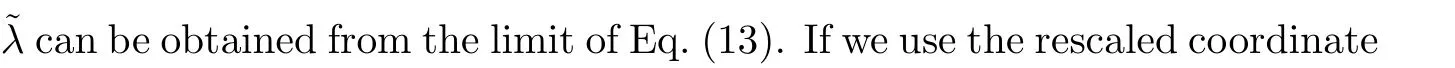

The corresponding large energy asymptotic eigenvalueλand wave functionsψ±(χ,ν)take the same functional form as the eigenvalue(7)and the wave functions(9),but with the coordinate variable substituted byχ.
Let us inspect more carefully the limit for eigenvalue and wave functions of the Lame equation.For the wave functions(15),we shift the argument byx→x+ω2,then take the limitq→0(i.e.withω1fixed,ω2→i∞)forψ±(x+ω2).The following expansions are needed,
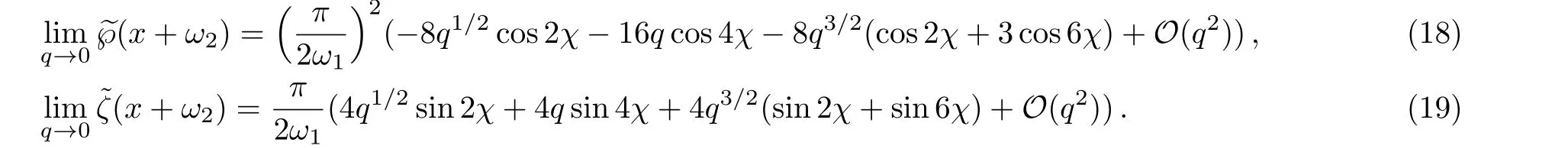
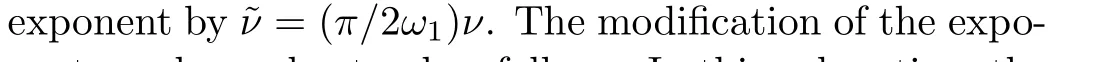
3 Small Energy Wave Function
3.1 Location of Small Energy Perturbation
Besides the large energy solution,there exists other solutions which are small energy excitations around local minima,i.e.the critical points of potential.We notice for some periodic potentials at each local minimum there is an asymptotic solution,and all known asymptotic solutions are located at a local minimum.[1,10]
For example,the potentialu(x)=2hcos2xhas local minima atx∗=0 andx∗=π/2 modulo periods.At the minimau(x∗)=±2h,therefore the eigenvalues take the form

whereδis the energy of small excitations.The small en-ergy perturbation is also the strong coupling solution for the potential,h≫1,see Refs.[6](Chapter V).In a similar way,the elliptic potentialu(x)=αe℘(x;2ω1,2ω2)has local minima atx∗=ωi,where the potentialu(x∗)=α(ei+ζ1),i=1,2,3.The first minima atx∗=ω1is associated to the large energy excitations already analyzed in the Subsec.2.3,the leading order energy comes from the quasimomentumλ∼−ν2+···The other two minima are associated to small energy perturbative solutions,nevertheless,in order to get compact formulae we should use the Jacobian form of the Lame equation to compute.
In this section we derive the corresponding strong coupling wave function,they have the Floquet form,and for elliptic potential their monodromies along periods 2Kand 2K+2K′indeed satisfy the relations we proposed in the previous paper.[1]
3.2 Mathieu Equation
The first small energy perturbation
Around the minimumx∗=0,λ=−2h+δ,the potential strengthh≫1 is large compared to the energyδ,therefore the expansion parameter ish1/2.The relationvx+v2=u+λhas an asymptotic solution in the form[1]

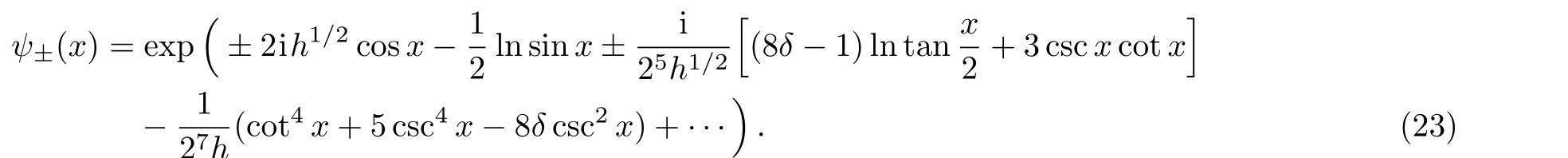
We can change the parameterδto the Floquet exponentν,by the following strong coupling expansion of the dispersion relation which is well known,[5−8]
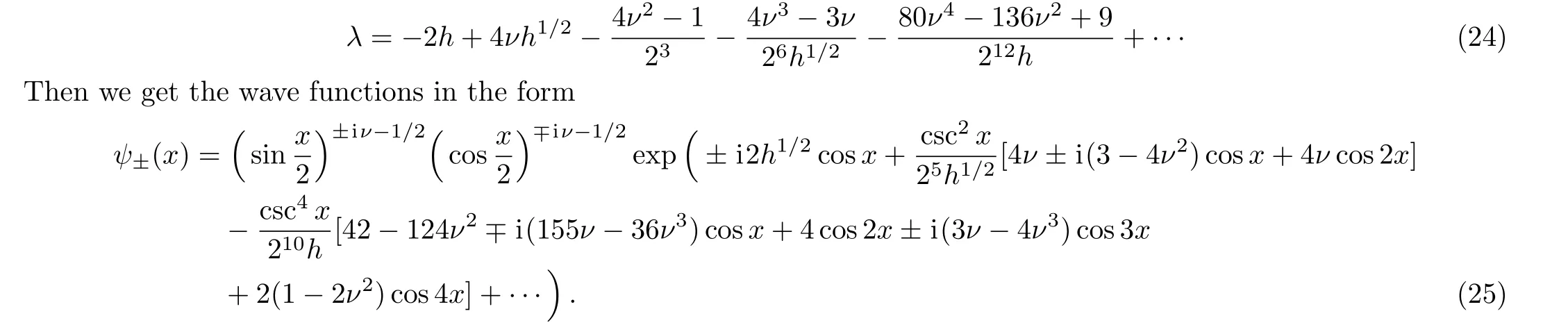
Because the wave functions are unnormalized,the terms in the exponent might appear in slightly different form,nevertheless the differences are constants and can be absorbed into the normalization constant.This comment applies to all of the asymptotic wave functions in this paper.When the exponentνtakes real value the asymptotic wave functions have the propertyψ∗±(x)=ψ∓(x).This solution seems often not recorded in the mathematical literature,however,it was analyzed in a paper by Stoner and Reeve.[12]The book Ref.[13]contains a discussion about this solution in the context of quantum mechanics.
The second small energy perturbation
Around the minimumx∗=π/2,λ=2h+δ,the potential strengthh1/2again serves as the expansion parameter.The relationvx+v2=u+λhas an asymptotic solution in the form(21),with

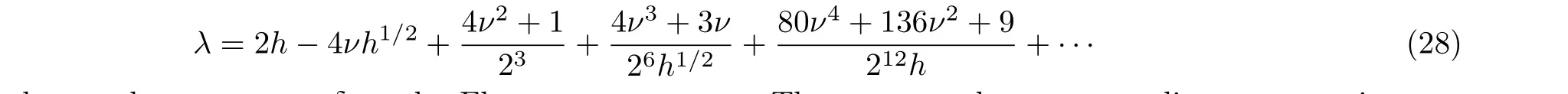
allows us to change the parameterδto the Floquet exponentν.Then we get the corresponding asymptotic wave functions
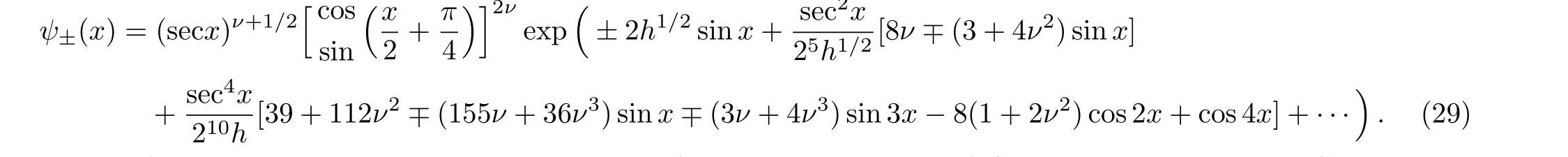
The dispersion relation at this local minimum[5−8]
The study of this solution dates back to the work of Ince and the work of Goldstein in the 1920s.Some recent materials easier to access include the paper by Dingle and Muller,[14]the books by McLachlan,[5]by Arscott[6]and by Muller-Kirsten.[13]
This asymptotic solution is related to the largehlimit of the standard Mathieu functions by
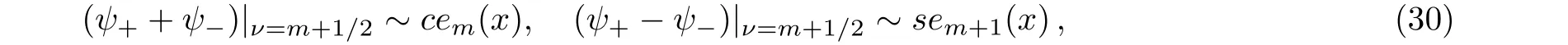
withmtakes either even or odd integers.[6]As we haveψ±(−x)=ψ∓(x),thencem(x)is an even function andsem(x)is an odd function,as desired.
3.3 Lame Equation
Now we turn to the more interesting case of elliptic potential where the advantage of our method becomes more transparent.As we have shown in Refs.[1,10],for small energy perturbative solution the Jacobian form of the elliptic function is more suitable,therefore we rewrite the potential asu(z)=αk2sn2(z|k2),and the Lame equation is

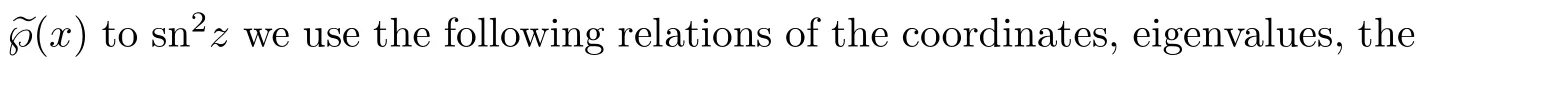
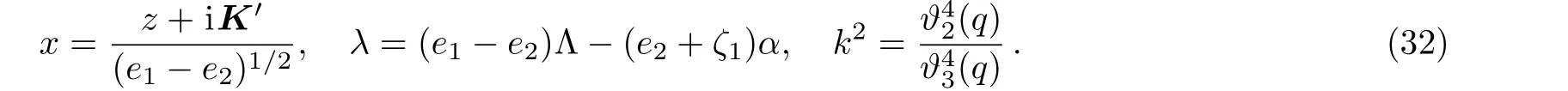
We also useµto denote the Floquet exponent throughout of this subsection,it is different from the Floquet exponentνused for the Weierstrass form.[10]
The locations of the small energy perturbations are given by two solutions of the condition∂zsn2z=0 atz∗=0 andz∗=Kwhich correspond tou(z∗)=0 andu(z∗)=αk2.
The first small energy expansion


In order to change the parameter Λ to the Floquet exponentµ,we use the widely known strong coupling expansion of the dispersion relation[6,8,13]
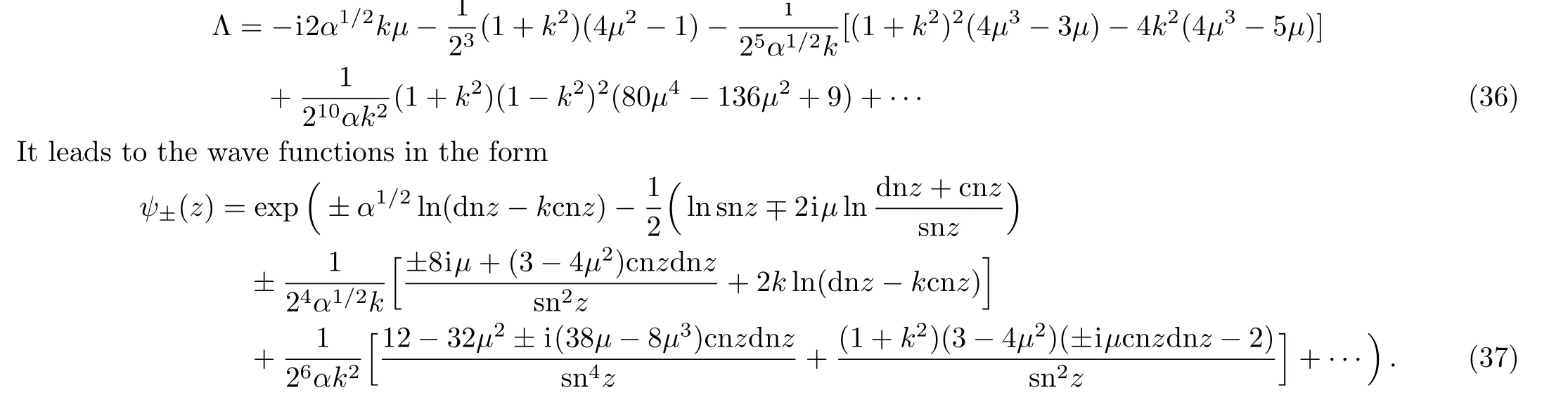
Only in the case when all quantities,including the elliptic modulusk,take real values we haveψ∗±(z)=ψ∓(z).In particular,up to the first two leading order the wave functions can be written as
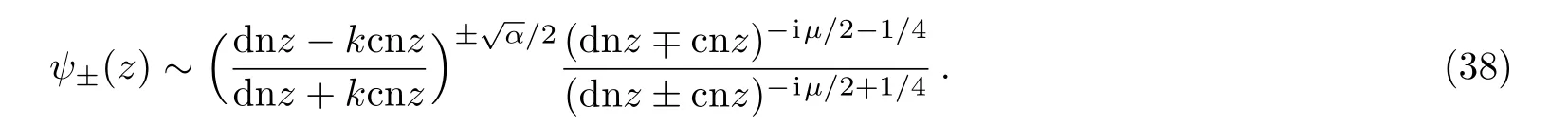
This asymptotic solution can be compared to the earlier results about the asymptotic Lame function obtained by Malurkar in the 1930s,and results by Muller in the 1960s.[13,15]
In the limitα→∞,k→0,µ→νwithα1/2k→2ih1/2finite,we recover the unnormalized wave functions,which differ some constant terms in the exponent from the asymptotic Mathieu wave functions(25).
The second small energy expansion

The corresponding dispersion relation has been missed for a long time in the literature,motivated by some ideas from quantum gauge theory[2]recently we have derived it by the WKB analysis and a duality argument,[10]then we rederive it using the method adopted in this paper.[1]It is
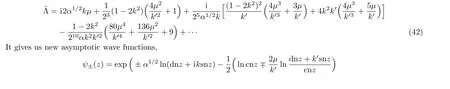

Taking the limit to the Mathieu wave functions(29),we would again encounter the difference of some constant terms,which can be absorbed into the normalization constant.
Up to now,everything about the small energy expansions for the Lame equation is consistent with the known results,although the monodromy relations,formulae(26)and(32)in Ref.[1],used to derive the corresponding dispersion relation remain a physics induced conjecture.
4 A Connection toN=2Gauge Theory
Now we come back to the original motivation which inspired our study to the spectral problem of periodic Schr¨odinger operators,especially for the elliptic potentials. As we have shown in Refs.[1,10],the asymptoticeigenvaluesof the Mathieu and the Lame equations are related to the solution of some deformedN=2 supersymmetric Yang-Mills gauge theories in the Nekrasov-Shatashvili limit(NS).[2]The three asymptotic spectral solutions are precisely i n accordance with three different dual descriptions of the low energy effective physics of gauge theory,i.e.the Seiberg-Witten duality,[16−17]in particular the large energy solution is related to the Nekrasov instanton partition function.[18]
The large energy asymptoticwave functionsare related to the instanton partition function of gauge theory with surface operator inserted.The partition function with surface operator extends Nekrasov’s localization formula,it is introduced and developed in Refs.[19–20].The computation can be carried out by the characters developed in Ref.[21].The paper by Alday and Tachikawa gives a detailed study about the relations between the SU(2)gauge theory with surface operator,the SL(2)conformal block and the two-body quantum Calogero-Moser model.[22]In the following,we brie fly explain the relation between the gauge theory partition function with surface operator and the asymptotic wave functions(9)and(15).
Let us start from the SU(2)N=2∗gauge theory with surface operator,whose partition function takes the following form,
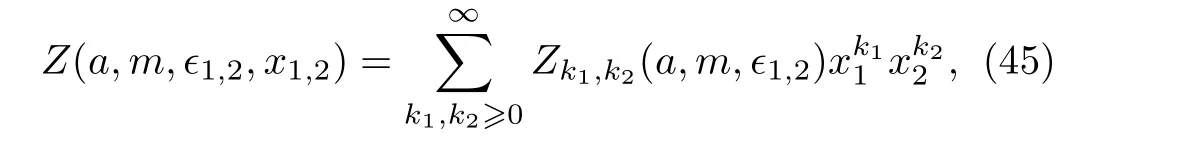
whereais the scalar v.e.v,mis the mass of adjoint matter,ϵ1,ϵ2are the Ω-deformation andx1,x2are the counting parameters.Written in the exponential form,its pole structure in the limitϵ1→0,ϵ2→0 is
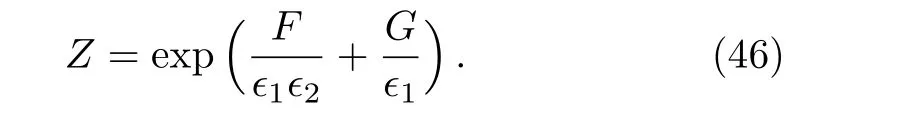

In order to relate gauge theory and the quantum mechanics spectral problem,some manipulations on the functionZare needed.The spectral solution of the Lame operator is related to the large-a-expansion of instanton partition function(46),in accordance with the large-νexpansions of the eigenvalue(13)and the eigenfunctions(15).BothF/ϵ1ϵ2andG/ϵ1containa-independent terms when expanded as large-a-series,which deserve special attention.These terms are polynomials ofx1,x2,and can be represented by the Dedekind eta function and the elliptic theta function,

To see the connections of functionsF,Gand the eigenvalue,eigenfunction,we first need to identify the parameters by

The elliptic nomeqis the instanton parameter of gauge theory,therefore,the functionFis anx-independentq-series which gives the eigenvalue,the functionGis aq-series depending on the coordinatexwhich gives the wave function.The eigenvalueλin(13)is related to the functionFin the limitϵ2→0 by
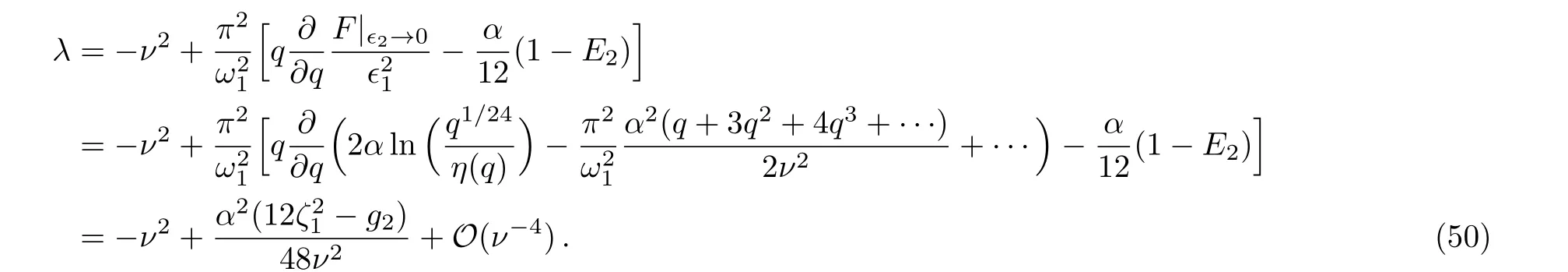
In gauge theory the term−ν2is perturbative,hence not included in the instanton partition function.This relation is examined in detail in Ref.[10](see formula(34)in that paper),there is a difference ofαζ1=α(π2/12ω21)E2on the right hand side because here we use the shifted potential e℘(x).
On the other hand,the wave functions(15)is related to the functionGin the limitϵ2→0 by
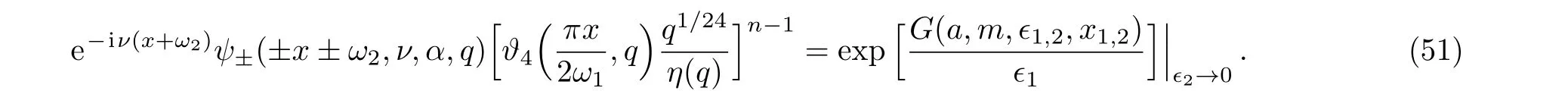
In the expression we emphasize the parameters used on both sides,and use the property of the large energy wave functionsψ−(−x−ω2)=ψ+(x+ω2).For example,up to the ordera−2we have
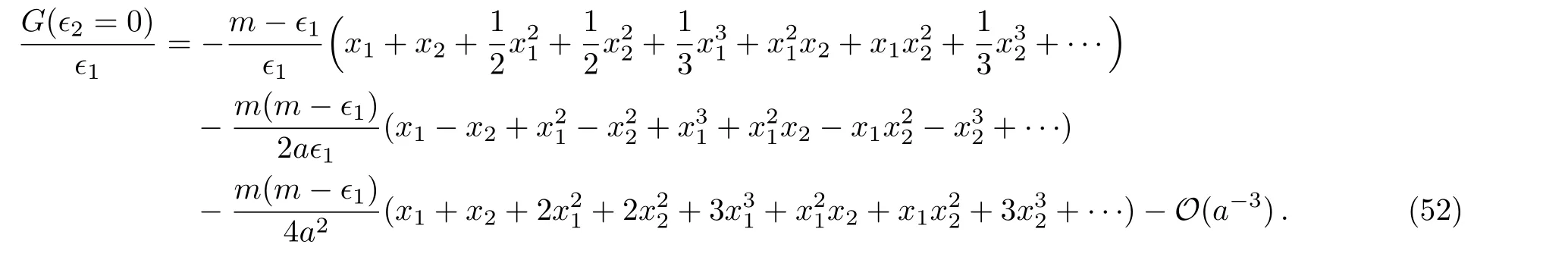
Using the relation of parameters given in Eq.(49),the first three pieces are summed into three elliptic functions,
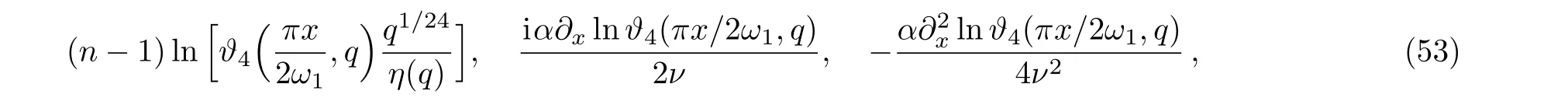
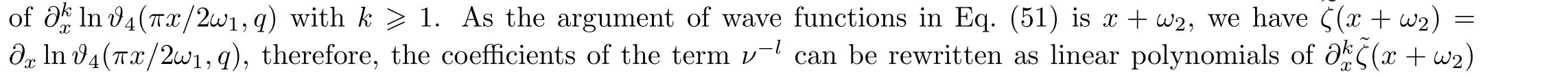
The eigenvalue(13)and the eigenfunction(15)provide an elliptic modular representation for the gauge theory partition function whenϵ2=0.In fact,we observe evidence that even for the case when both deformation parameters are turned on,ϵ1/=0,ϵ2/=0,the instanton partition function with surface operator can be expressed in terms of theta functions.This property indicates the instanton partition function secretly records relations to the elliptic curve.Indeed,this connection can be seen from the point of view of either integrable system[2]or conformal field theory.[22−23]
In the decoupling limit,theN=2∗gauge theory becomes the pure gauge theory.The corresponding partition function with surface operator can be found in Ref.[24],it is related to the asymptotic Mathieu wave functions(9).
Appendix A:A Matrix that Counts Divisors of Integers
When we take thea→∞limit of the instanton partition with surface operator,onlya-independent terms in the functionsFandGremain.These terms are represented by two elliptic modular functions,
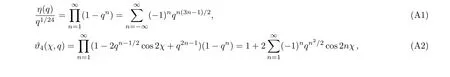
withχ=πx/2ω1.Had we expanded them asq-series as usual,there might not be interesting things deserve to say.Nevertheless,if we rewrite them in terms ofx1,x2as given in Eq.(49),and then expand minus of the logarithm of them as series ofx1,x2,we get

The coefficient matrix Θ4[i,j]is a symmetric in finite matrix with all elements positive,as a digest here we present thefirst 22 dimensions.Notice that the numbers for rows and columns of the matrix begin from 0.

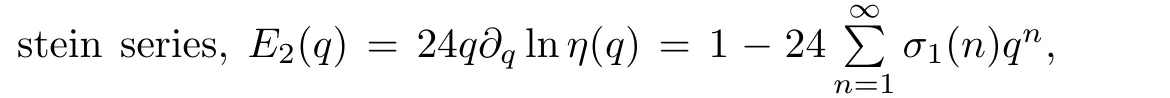

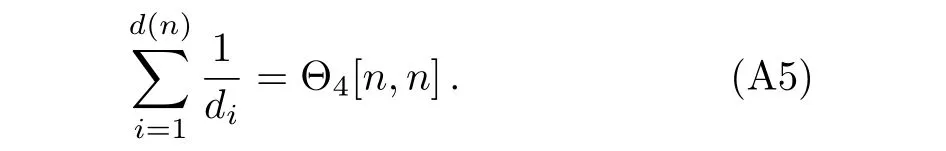
For example,in the 18-th row we have the divisor functionσ−1(18),
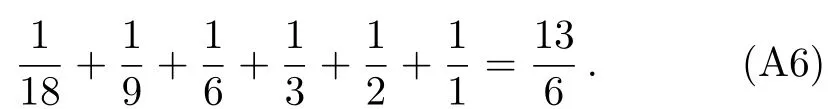
This fact indicates a relation of the eta function and the theta function expanded as in(A3),(A4):while the logarithm of eta function knows the in finite sequence of numbers 1,3/2,4/3,7/4,...,the logarithm of theta function diagnoses where they come from.It is the same in spirit for the situation in gauge theory:while the instanton partition function without surface operator knows the eigenvalue expansion,it is the instanton partition function with surface operator tells the whole story.

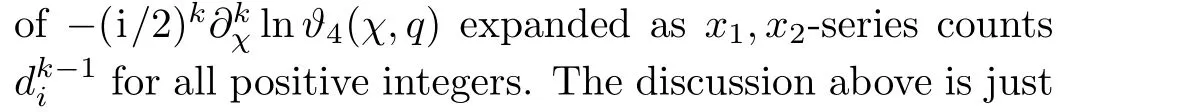
This might be a folklore of number theory,nevertheless,it is strange instanton knows it.
5 Acknowledgments
I thank Institute of Modern Physics at Northwest University,Xi’an,during the summer school“Integrable models and their applications 2016”where this work is finalized.Part of the work has been done when I was supported by the FAPESP No.2011/21812-8,through IFT-UNESP.
[1]W.He,Commun.Theor.Phys.69(2018)115.
[2]N.Nekrasov and S.Shatashvili,Quantization of integrable systems and four dimensional gauge theories,in16th International Congress on Mathematical Physics,World Scientific,Singapore(2010)265.
[3]R.M.Miura,C.S.Gardner,and M.D.Kruskal,J.Math.Phys.9(1968)1204.
[4]O.Babelon,D.Bernard,and M.Talon,Introduction to Classical Integrable Systems,Cambridge University Press,Cambridge(2003).
[5]N.W.McLachlan,Theory and Application of Mathieu Functions,Oxford University Press,Oxford(1947).
[6]F.M.Arscott,Periodic Differential Equations,Pergamon Press,Oxford(1964).
[7]Z.X.Wang and D.R.Guo,Special Functions,World Scientific,Singapore(1989).
[8]NIST Digital Library of Mathematical Functions,F.W.J.Olver,A.B.Olde Daalhuis,D.W.Lozier,et al.,eds.http://dlmf.nist.gov.
[9]E.Langmann,An Explicit Solution of the(Quantum)Elliptic Calogero-Sutherland Model,inSymmetry and Perturbation Theory(Cala Gonone),World Scientific,Singapore(2005)159.
[10]W.He,J.Math.Phys.56(2015)072302.
[11]W.He,Ann.Phys.353(2015)150.
[12]M.Stoner and J.Reeve,Phys.Rev.D 18(1978)4746.
[13]H.J.W.Muller-Kirsten,Introduction to Quantum Mechanics:Schr¨odinger Equation and Path Integral,World Scientific,Singapore(2006).
[14]R.B.Dingle and H.J.W.Muller,Journal fur Die Reine und Angewandte Mathematik 211(1962)11.
[15]H.J.W.Muller,Math.Nachr.31(1966)89.
[16]N.Seiberg and E.Witten,Nucl.Phys.B 426(1994)19.
[17]N.Seiberg and E.Witten,Nucl.Phys.B 431(1994)484.
[18]N.Nekrasov,Adv.Theor.Math.Phys.7(2004)831.
[19]A.Braverman,Instanton Counting via Affine Lie Algebras I:Equivariant J-functions of(Affine)Flag Manifolds and Whittaker Vectors,Proceedings of the CRM Workshop on Algebraic Structures and Moduli Spaces(Montreal),American Mathematical Society,Providence(2004)[arXiv:math/0401409].
[20]A.Braverman and P.Etingof,Instanton counting via affine Lie algebras II:from Whittaker Vectors to the Seiberg-Witten Prepotential,[arXiv:math/0409441].
[21]B.Feigin,M.Finkelberg,A.Negut,and L.Rybnikov,Selecta Mathematica 17(2011)513.
[22]L.F.Alday and Y.Tachikawa,Lett.Math.Phys.94(2010)87.
[23]L.F.Alday,D.Gaiotto,and Y.Tachikawa,Lett.Math.Phys.91(2010)167.
[24]H.Awata,H.Fuji,H.Kanno,et al.,Adv.Theor.Math.Phys.16(2012)725.
杂志排行
Communications in Theoretical Physics的其它文章
- Thermodynamic Nonequilibrium Features in Binary Diffusion∗
- Ordinary Mode Instability in a Cairns Distributed Electron Plasma
- Thermal Conductivity of Complex Plasmas Using Novel Evan-Gillan Approach
- Spontaneous Emission Originating from Atomic BEC Interacting with a Single-Mode Quantized Field
- Molecular Dynamics Simulations of the Elastic Anisotropy of Pd at Extreme Conditions∗
- In fluences of Crystal-Field and Interlayer Coupling Interactions on Dynamic Phase Diagrams of a Mixed-Spin(3/2,2)Bilayer System∗
