A Novel Method to Solve Nonlinear Klein-Gordon Equation Arising in Quantum Field Theory Based on Bessel Functions and Jacobian Free Newton-Krylov Sub-Space Methods
2018-06-15ParandandNikarya
K.Parand and M.Nikarya
Department of Computer Sciences,Shahid Beheshti University,G.C.,Tehran,Iran
1 Introduction
The nonlinear Klein-Gordon equation arises in many scientific areas such as electromagnetic interactions,the relativistic hydrogen spectrum,coulomb scattering,nonlinear optics,solid state physics and quantum field theory etc.[1−3]The Klein-Gordon equation plays the role of one of the fundamental equations of quantum field theory. This equation describes relativistic electrons and is a quantized version of the relativistic energy momentum relation.[4−6]This equation was first considered as a quantum wave equation for an equation describing de Broglie waves,[1,4,7]also has a great importance in relativistic quantum mechanics,which is used to describe spinless particles.The nonlinear Klein-Gordon equation has the general form:[8−9]

and with the Dirichlet or Neumann type boundary conditions,whereτ,α,γare known constants.Equation(1)is called Klein-Gordon with quadratic nonlinearity ifk=2,with cubic nonlinearity ifk=3.The numerical study of the nonlinear Klein-Gordon equation has been carried out for last half Century and still it is an active area of research to develop some better numerical schemes to approximate its solution.In the past decades many researchers have solved this problem.[5,10−18]Recently,several numerical techniques have been developed for solving the Klein-Gordon equation(1),for example Luoet al.have solved this problem by using a fourth-order compact and conservative scheme,they discretized using the integral method with variational limit in space and the multidimensional extended Runge-Kutta method in time.[19]Vermaet al.have proposed a numerical scheme based on forward finite difference,QLM process and DQ method,[9]Bhrawy and Soubhy by using Legendre Gauss-Lobatto collocation solve linear and nonlinear Klein-Gordon.[20]Aimi and Panizzi have solved 1D Klein-Gordon equation by using boundary element- finite element method coupling procedure.[7]Razaet al.have solved nonlinear Klein-Gordon equation using Sobolev gradients.[21]Donget al.[22]by using a time-splitting Fourier pseudo-spectral discretization solved this problem.Guo and Wang have solved this problem by using collocation method based on Jacobi polynomials.[23]Bao and Dong have solved this problem by using finite difference method.[24]Kumaret al.have introduced numerical computation by using Homotopy analysis method to solve Klein-Gordon equation.[25]Biswaset al.have found traveling wave solutions of the nonlinear dispersive Klein-Gordon equation.[26]Hussainet al.have solved this problem by meshless method and method of lines.[27]Jang[28]has solved this problem by using semi-analytical method.Jiwari[29]has solved this problem by Lagrange interpolation and modified cubic B-spline differential quadrature methods.Shaoa and Wu have introduced a numerical solution of the nonlinear Klein-Gordon equation using the Chebyshev tau meshless method.[30]Pekmen and Tezer-Sezgin have solved this problem by using DQM.[8]Chang and Liu have introduced an implicit Lie-group iterative scheme to solve this problem.[31]Guoet al.have solved this problem by element-free kp-Ritz method.[32]Mohebbiet al.have introduced a method based on applying fourth order timestepping schemes in combination with discrete Fourier transform to solve Klein-Gordon equation.[33]
Now in this paper,we intend to solve the Klein-Gordon equation using a novel method based on Bessel functions of the first kind,spectral collocation method and Jacobian free Newton-Krylov sub-space methods.Recently,Bessel functions have been used to solve nonlinear ODE,IDE,and fractional differential equation,[34−36]now we want to use them to solve nonlinear PDE namely Klein-Gordon equation.The rest of this paper is organized as follows:the function approximation,Bessel functions and spectral methods are introduced in Sec.2.In Sec.3 the JFNGMRes with adaptive preconditioner is described to solve nonlinear systems of algebraic equations.Then to show the advantages,applicability and reliability of proposed method we solve some examples of Klein-Gordon equation and compare our results with others in Sec.4.Finally,the paper concludes in Sec.5.
2 Function Approximation and Spectral Methods Based on Bessel Functions
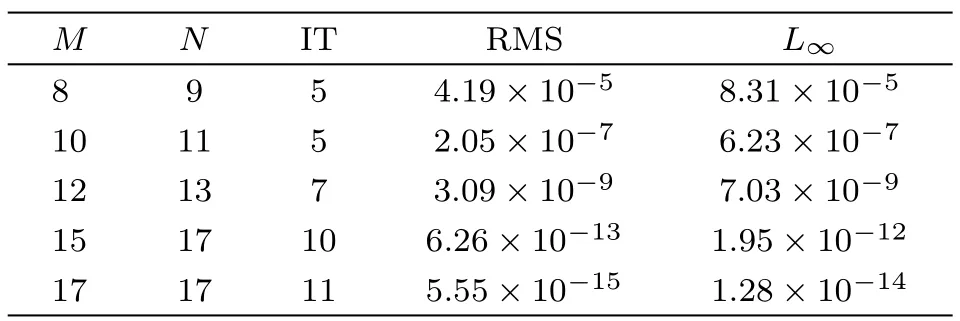
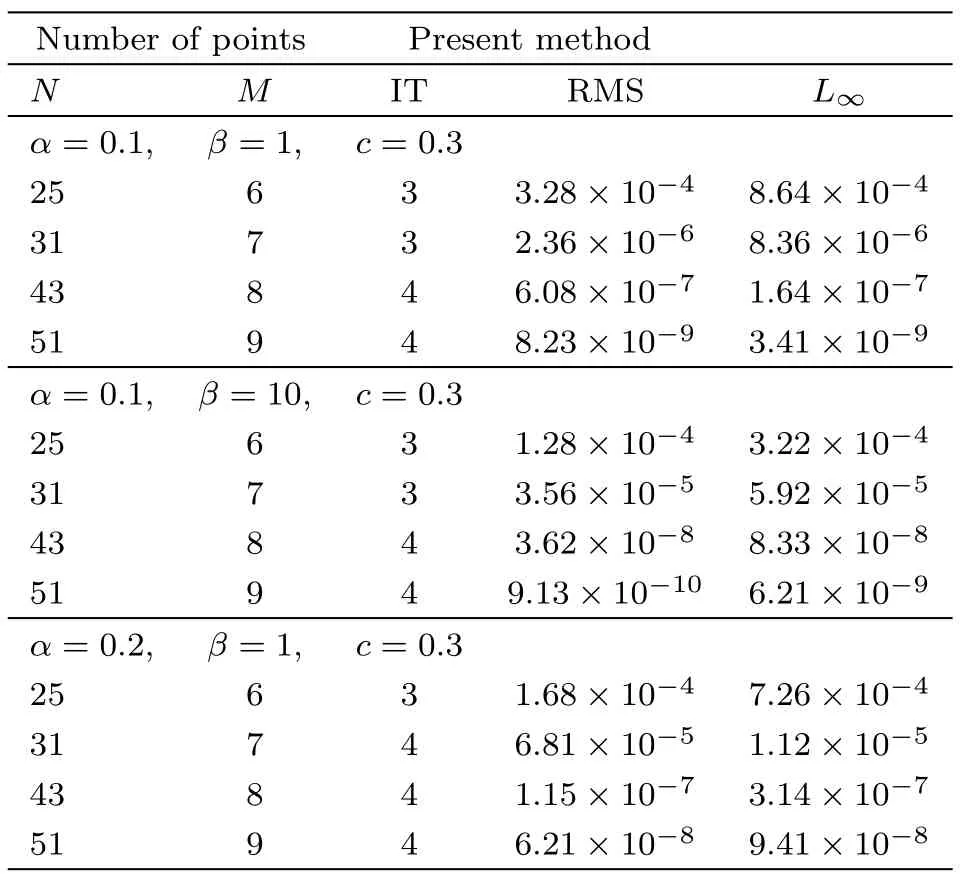
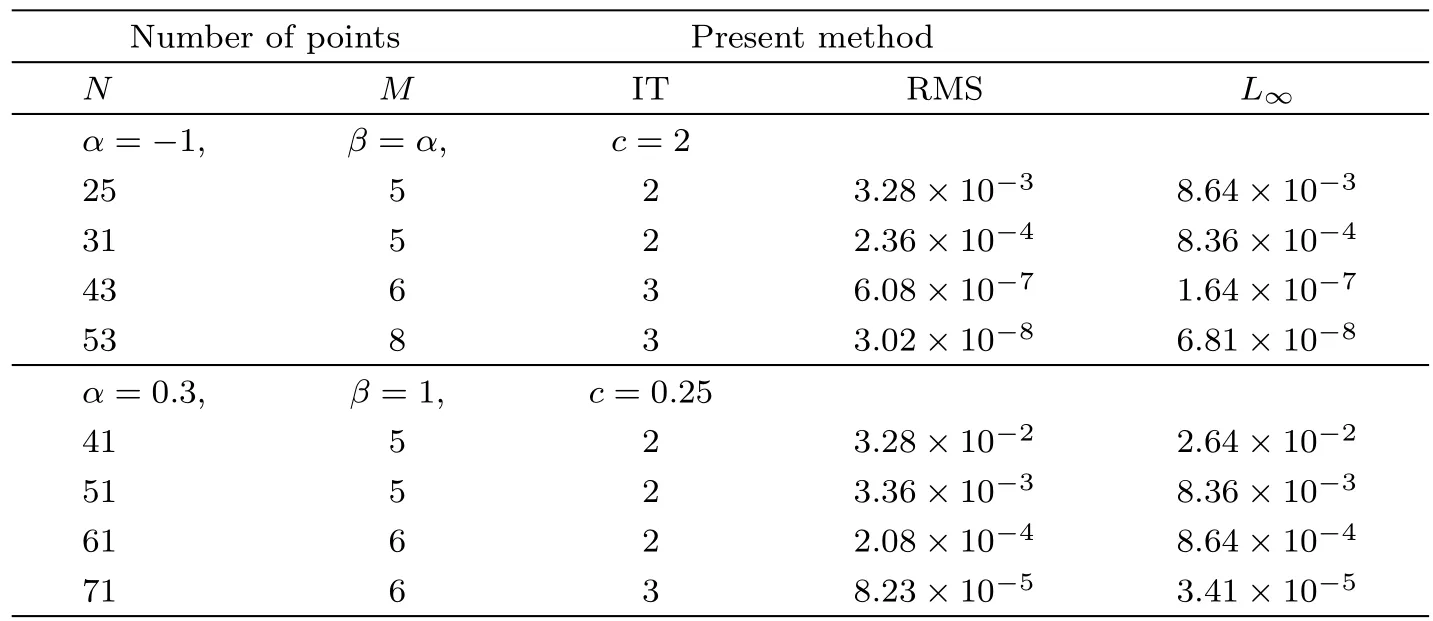
Definition 1Let Λ={x|a For any realr≥0,we define the spaceHrω(Λ)by the space interpolation as in Adams.[37] In this paper we use Bessel function of the first kindJn(x)as the basis functions ofL2(Λ): Series(2)is convergent for all−∞ ProofBy deriving Eq.(2)and using expansions ofJn−1(x)andJn+1(x),the result is desirable. Remark 1The derivative operational matrix of the first kind Bessel functions can be as follow: LetJ= [J0(x),J1(x),J2(x),...,Jn(x)]TthereforeJ′=DJ,whereDis derivative operational matrix and is obtained by using Eq.(4): where thea0,a1,a2,....,anwill be obtained by an interpolation technique. LetNbe a positive integer,we define space Several papers have discussed about convergence of spectral methods[39−42]and spectral methods to solve nonlinear Klein-Gordon equation.[43−44]In a same way we can write about convergence of proposed method to solve Klein-Gordon equation as follows. Remark 2Assume that theu∈L2(0,T;Hr(Λ)),r>1,is the solution of the Klein-Gordon equation(1),and theuN=PNu∈JN(Λ)×JN(0,T)is the approximation ofu,then: andCis a positive constant depending only on the norms ofuin the spaces mentioned.[41,45]We know that,theJN(Λ)×JN(0,T)is a finite subspace ofHr(Λ)×L2(0,T),according to the assumptionu∈Hr(Λ)×L2(0,T),the∥u∥= ∫T0∥u∥2r,ωdt<∞,therefore,there is anN0∈N that for anyN>N0,Nrbe bigger than∥u∥or equivalentlyC.So,ifNbe large enough,we can say:ifN−→∞then∥u−uN∥Hr(Λ)×L2(0,T)−→0,hence,the error of this approximation by increasingNwill be decreased.In numerical examples this principle will be shown. Spectral methods,in the context of numerical schemes for solving differential equations,generically belong to the family of weighted residual methods(WRMs).[46]WRMs represent a particular group of approximation techniques,in which the residuals(or errors)are minimized in a certain way and thereby leading to specific methods including Galerkin,Petrov-Galerkin,collocation,and tau formulations.Consider the approximation of the following problem via spectral method: whereLis the differential or integral operation,Nis a lower-order linear and/or nonlinear operator involving only derivatives(if exist)andf(x,t)is a function of variablesxandt,with enough initial and boundary conditions.The starting point of the spectral methods is to approximate the solutionu(x,t)by a finite summation: whereϕn’s are the basis functions that we have chosenJn(x)as basis function and the expansion’s coefficients must be determined.SubstitutinguwithuM,Nin Eq.(7)leads to the residual function: where{ψk}are test functions,andωis positive weight function. The choice of test functions results to a kind of the spectral methods.[47−48]A method for forcing the residual function(9)to zero,is the collocation algorithm.[35−36,49]In this method,by choosing Lagrange basis polynomials as test function,such thatψj(x)=Lj(x)and using Gauss quadrature rule in Eq.(11)we can write:[46] In this paper,since the PDE(7)is nonlinear,the obtained system of equations(13)is nonlinear,too.In next section,we will describe how to solve this nonlinear system of equations. Solving a nonlinear differential equation by spectral method directly(without linearization or discritization)leads to solving a nonlinear system of algebraic equationsF(x)=0,whereF:Rn→Rnis a functionF(x)=(f1(x),f2(x),f3(x),...,fn(x))Tandx∈Rnis a vector.So speed and accuracy of solving this nonlinear system is very important.Many works have been done to improve solving the nonlinear systems.[50−54]One of the best methods to solve a nonlinear system is classical Newton’s iterative method: whereF′(x)=J(x)is then×nJacobian matrix.Therefore: In spectral methods to increase the accuracy,the number of equations must be increased,so often size of system of equation is large.But for large and complicated nonlinear systems,calculation and reorderingJ(xn)and solving obtained linear system in each iteration could be mostly time consuming.Hence,there are some improvements in Eq.(16),whereJ(xn)is calculated and linear system will be solved.For example some mathematicians used a fixed Jacobian matrix in every iteration or used different linear solver with several preconditioners.One of the good ideas,is to use the finite difference technique to approximate Jacobian-vector product: whereεis a very small value.Jacobian-vector product,can be useful to approximate Jacobian matrix and matrixvector product.Also,for large dimensions,iterative methods such as GMRes or BiCGSTAB are preferred over direct solvers.[54−55]In this paper,a Jacobian-free Newton GMRes(JFNGMRes)with an adaptively preconditioner have been used to solve large nonlinear system of equations.This preconditioner has been introduced by Saad[53]and used in Ref.[54].Using this finite difference technique and updating adaptive preconditioning improve the computations in Newton’s method and GMRes.[53−54]Many researchers have used Newton-Krylov methods and Jacobian free Newton-Krylov methods to solve several nonlinear problems.[53−57] In this section we describe the Jacobian free Newton’s method alongside generalized minimum residual with adaptive preconditioner Begin 1.Setk=0(iteration counter of Newton method)and an initial guessx0. 2.Select a nonsingular MatrixM0=ηIas the preconditioner,whereη∈R andIn×n=diag(1,...,1) 3.Begin ofNewton’siterations:repeat until∥F(xk)∥2 4.Use GMRes method with Jacobian free formula to solve linear systemJ(xk)δk=F(xk). In Refs.[53–54]inner and outer preconditionersMilnandMkand how to help it to Newton-Krylov method have been discussed. To show the accuracy,availability,reliability and convergent rate of present method to solve Klein-Gordon equation,several examples of Klein-Gordon equation will be solved in this section.To obtain the solutions,we first transfer the solving the nonlinear Klein-Gordon equation to a nonlinear system of algebraic equations by using collocation spectral method based on Bessel function of the first kind without any discritization and linearization methods.Then we solve this nonlinear algebraic system by using JFNGMRes method and acquire the solution of this PDE.In solving procedure of all examples that follow in this paper,we use roots of shifted Legendre polynomialPn(x)as collocation points,and satisfy the initial conditions by adding and multiplying some terms to the basis functions,satisfy the boundary conditions in the nonlinear system of equations and the initial guess of the iterative JFNGMRes method is vector[0,0,...,0]T.Also,some error definitions used in this article are as bellow: Example 1Consider the Klein-Gordon equation(1)with quadratic nonlinearity as follows: subject to the initial conditions: This example has been solved by using proposed method withM=17,N=17 and 11 JFNGMRes iteration.To show efficiently and reliability of presented method,obtained results is compared with results of DQ method,[8]a method based on the tension spline function and finite difference approximations[5]and radial basis functions collocation method[14]in Table 1.Also to show convergence rate and accuracy of proposed method,we use the RMS andL∞errors,this results are shown in Table 2,this table shows that by increasing the collocation points the errors will be decreased rapidly also the number of iterations(IT)will be increased. Table 1 Comparison of obtained results of presented method with N=17,M=17 and 11 JFNGMRes iterations,and results of Refs.[5,8,14]for example 1. Table 2 The convergence rate of presented method to solve example 1. Example 2 Consider the kink wave equation of Klein-Gordon equation(1)as follows: The exact solution of this equation is: Fig.1 The obtained graphs of solution for example 2 for c=0.3 and several α,β.(a)α =0.1,β =1;(b)α =0.2,β=1;(c)α=0.1,β=10. Table 3 Comparison of presented method and results of B-spline DQ method[29]for solving kink wave equation with α =0.2,β =1 and c=0.3. Table 4 Error and convergence rate of presented method for solving kink wave equation with different number points. Example 3 Consider the following single soliton equation of Eq.(1): The exact solution of this equation is: In this paper a new numerical algorithm was proposed to solve nonlinear Klein-Gordon equation.This method uses the spectral collocation method,the Bessel functions of the first kind as basis function and roots of the shifted Legendre polynomials as collocation point to convert nonlinear Klein-Gordon equation to a nonlinear system of algebraic equations.Then this nonlinear system is solved by using the Jacobian free Newton and GMRes methods with an adaptive preconditioner updated in each iteration.The obtained nonlinear system from spectral methods usually is large and ill-condition,therefore,iterative methods such as GMRes are preferred over direct solvers.Now we use an adaptive preconditioner to enhance the convergent rate of JFNGMRes.As indicated in the presented examples,the solutions of the nonlinear systems are obtained in 3,4 and 11 Newton iterations,also in all examples the initial guess of JFNGMRes is simple vector[0,0,...,0]T,that show the speed and power of the proposed method.Also the shown RMS andL∞errors in the presented tables and comparison with others methods show efficiently,applicability and reliability of collocation method based on the Bessel functions of the first kind.Some advantages of the presented method include high convergence rate of collocation method based on Bessel functions of the first kind to solve Klein–Gordon equation,few iterations for Newton method,simple initial guess for JFNGMRes method and no need for discretization and linearization and saving memory and processing.In general in this paper there are some novelties:(i)Using Bessel function as basis function in spectral methods to solve nonlinear PDE.(ii)Using spectral methods without any time discritization and linearization method to solve Klein-Gordon equation.(iii)using Jacobian free Newton method with adaptive preconditioned GMRes in spectral methods to solve Klein-Gordon equation. Fig.2 Obtained graphs of single soliton solution.(a)α=β=−1,c=2;(b)α=0.3,β=1,c=0.25. Table 5 Obtained results and convergence rate of presented method with and 4 JFNG iteration for several α,β and c=2 for single soliton problem at t=1. Acknowledgments The corresponding author would like to thank Shahid Beheshti University for the awarded grant. [1]C.Itzykson and J.B.Zuber,Quantum Field Theory,McGraw-Hill International Book Co,New York(1980). [2]S.Weinberg,Quantum Theory of Fields,Cambridge University Press,Cambridge(1995). [3]M.Rahman,S.Dulat,and K.Li,Commun.Theor.Phys.54(2010)809. [4]W.Greiner,Relativistic Quantum Mechanics Wave Equations,Springer,Berlin(2000). [5]J.Rashidinia and R.Mohammadi,Comput.Phys.Commun.181(2010)78. [6]G.L.Xun and P.J.Ting,Commun.Theor.Phys.50(2008)1276. [7]A.Aimi and S.Panizzi,Numer.Methods Partial Differ.Equ.30(2014)2042. [8]B.Pekmen and M.Tezer-Sezgin,Comput.Phys.Commun.183(2012)1702. [9]A.Verma,R.Jiwari,and S.Kumar,Int.J.Numer.Methods Heat Fluid Flow24(2014)1390. [10]A.M.Wazwaz,Commun.Nonlinear Sci.Numer.Simul.13(2008)889. [11]S.Abbasbandy,Int.J.Methods Eng.70(2007)876. [12]S.Mohyud-Din and A.Yildirim,J.Appl.Math.Stat.Inform.(JAMSI)6(2010)99. [13]B.Y.Guo,X.Li,and L.Vazquez,Math.Appl.Comput.15(1996)19. [14]M.Dehghan and A.Shokri,J.Comput.Appl.Math.230(2009)400. [15]M.A.M.Lynch,J.Comput.Appl.Math.31(1999)173. [16]S.Li and L.Vu-Quoc,SIAM J.Numer.Anal.32(1995)1839. [17]S.Machihara,Funkcial.Ekvac.44(2001)243. [18]N.Masmoudi and K.Nakanishi,Math.Ann.324(2002)359. [19]Y.Luo,X.Li,and C.Guo,Numer.Methods Partial Differ.Equ.33(2017)1283. [20]A.H.Bhrawy and S.I.El-Soubhy,J.Comput.Theor.Nanosci.12(2015)3583. [21]N.Raza,A.R.Butt,and A.Javid,J.Funct.Spaces 1(2016)1. [22]X.Dong,Z.Xu,and X.Zhao,Commun.Comput.Phys.16(2014)440. [23]B.Y.Guo and Z.Q.Wang,Adv.Comput.Math.40(2014)377. [24]W.Bao and X.Dong,Numer.Math.120(2012)189. [25]D.Kumar,J.Singh,S.Kumar,and J.Sushila,Alexandria Eng.J.53(2014)469. [26]A.Biswas,C.M.Khalique,and A.R.Adem,J.King Saud Uni.24(2012)339. [27]A.Hussain,S.Haq,and M.Uddin,Eng.Anal.Boundary Elem.37(2013)1351. [28]T.S.Jang,Appl.Math.Comput.243(2014)322. [29]R.Jiwari,Comput.Phys.Commun.193(2015)55. [30]W.Shaoa and X.Wua,Comput.Phys.Commun.185(2014)1399. [31]C.W.Changa and C.S.Liu,Appl.Math.Model.40(2016)1157. [32]P.Guo,K.Liew,and P.Zhu,Appl.Math.Model.39(2015)29172928. [33]A.Mohebbi,Z.Asgari,and A.Shahrezaee,Z.Naturforsch.A 66(2011)735. [34]K.Parand,M.Nikarya,J.A.Rad,and F.Baharifard,Zeit.Natur.A 67(2012)665. [35]K.Parand,J.A.Rad,and M.Nikarya,Int.J.Comput.Math.91(2014)1239. [36]K.Parand,J.A.Rad,and M.Nikarya,J.Comput.Theor.Nanosci.11(2014)131. [37]R.A.Adams,Sobolev Spaces,Academic Press,New York(1975). [38]W.W.Bell,Special Functions For Scientists And Engineers,D.Van Nostrand Company,London(1967). [39]B.Y.Guo,Spectral Methods and Their Applications,World Scientific,Singapore,River Edge,N.J.(1998). [40]E.Weinan,SIAM J.Numer.Anal.29(1992)1520. [41]K.Atkinson,O.Hansen,and D.Chien,Numer.Algorithms 63(2013)213. [42]D.Gottlieb,L.Lustman,and E.Tadmor,SIAM J.Numer.Anal.24(1987)532. [43]X.Li and B.Guo,J.Comput.Mathema.15(1997)105. [44]I.J.Lee,J.Korean Math.Soc.32(1995)541. [45]B.Guo,J.Math.Anal.Appl.243(2000)373. [46]J.Shen,T.Tang,and L.L.Wang,Spectral Methods:Algorithms,Analysis and Applications,Springer,Berlin,Heidelberg(2011). [47]K.Parand,M.Delkhosh,and M.Nikarya,Tbilisi Mathematical J.10(2017)31. [48]J.A.Rad,K.Parand,and S.Kazem,Int.J.Appl.Comput.Math.3(2017)919. [49]K.Parand and M.Nikarya,Eur.Phys.J.Plus 132(2017)496. [50]G.M.Shro ffand H.B.Keller,SIAM J.Numer.Anal.30(1993)1099. [51]A.Cordero,J.L.Hueso,E.Martinez,and J.R.Torregrosa,J.Comput.Appl.Math.233(2010)2696. [52]G.H.Nedzhibov,J.Comput.Appl.Math.222(2008)244. [53]A.Soulaimani,N.B.Salah,and Y.Saad,Int.J.Comput.Fluid Dynam.16(2002)1. [54]Y.Chen and C.Shen,IEEE Trans.Power Syst.21(2006)1096. [55]H.Asgharzadeh and I.Borazjani,J.Comput.Phys.331(2017)227. [56]D.Knoll and D.Keyes,J.Comput.Phys.193(2004)357. [57]A.Hajizadeh,H.Kazeminejad,and S.Talebi,Prog.Nucl.Energy 95(2017)48.




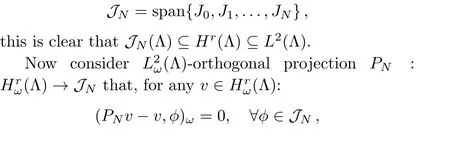
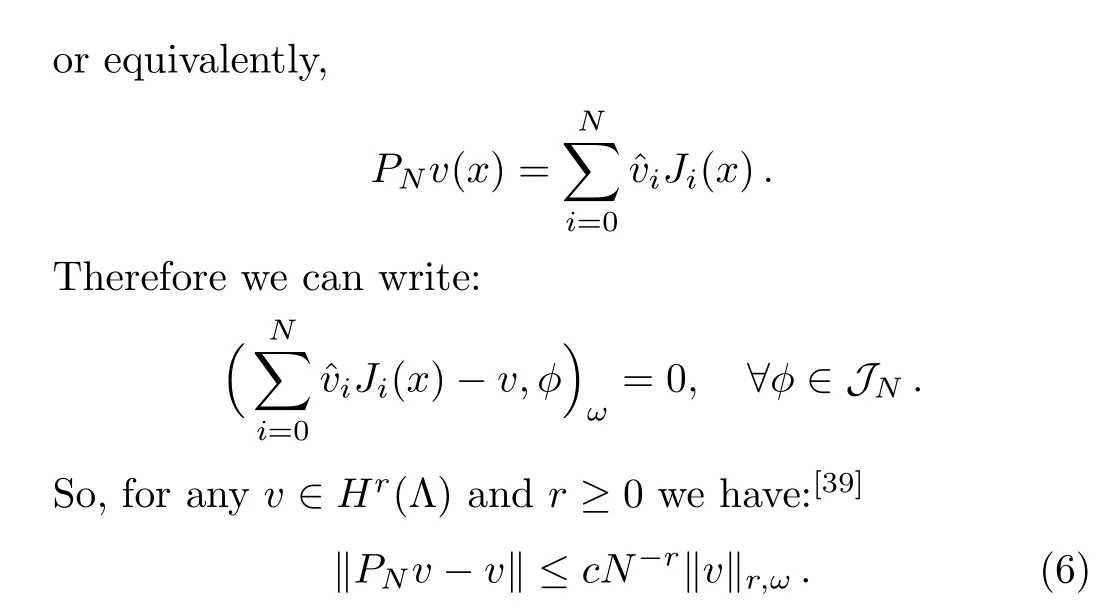

2.1 Spectral Collocation Method
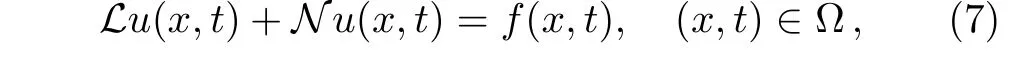
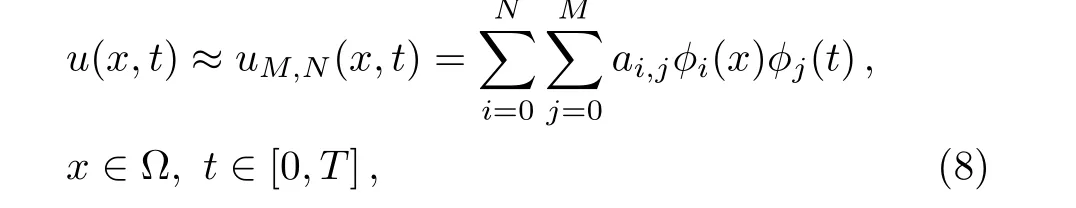
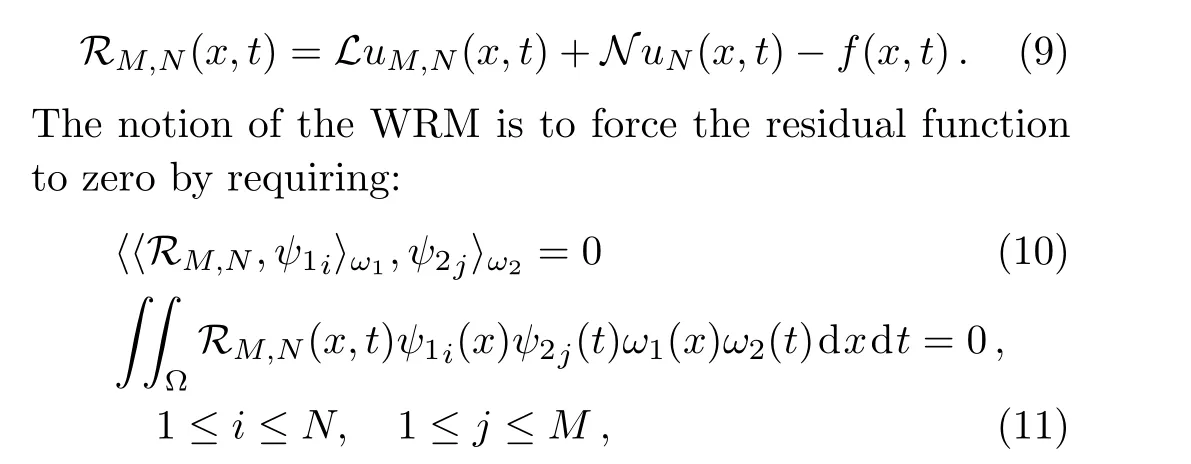
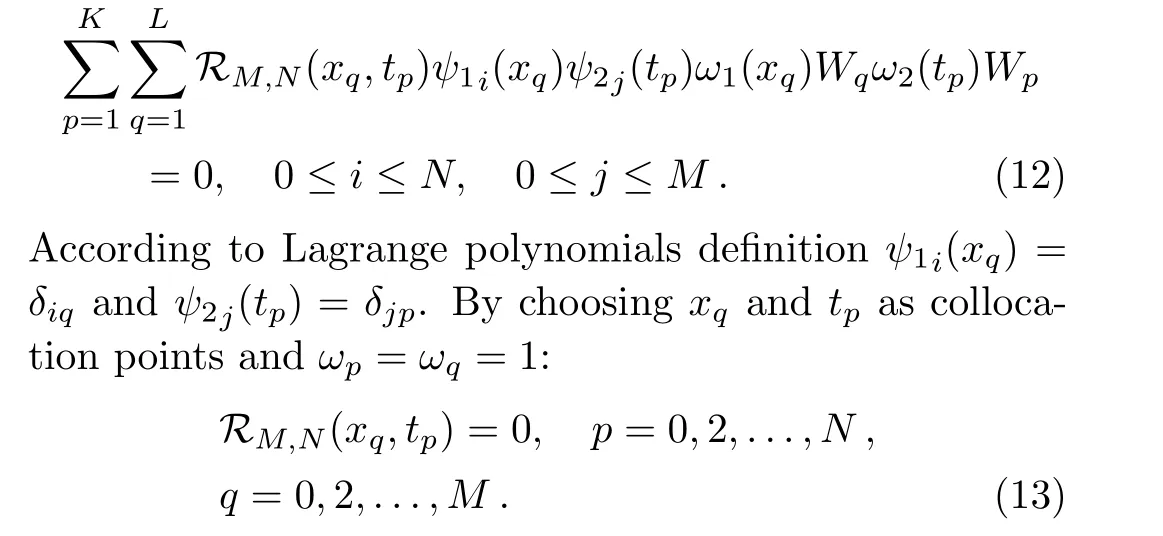
3 Newton-Krylov Algorithm
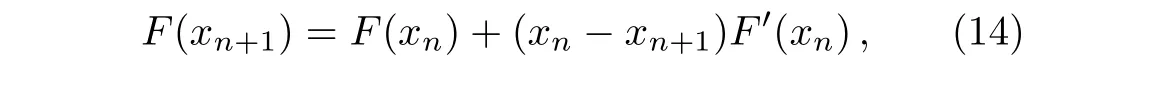

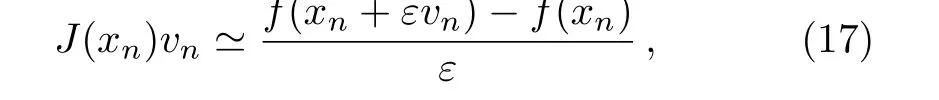

4 Solving Some Examples of Nonlinear Kilen-Gordon Equation

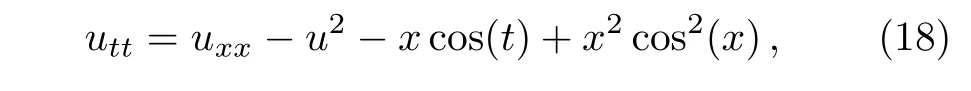







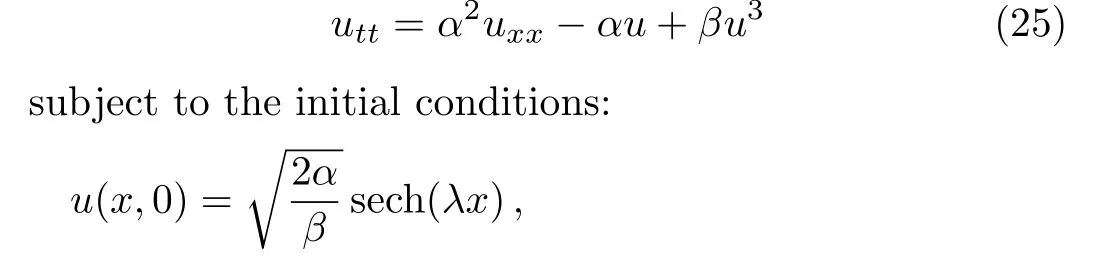



5 Conclusions

杂志排行
Communications in Theoretical Physics的其它文章
- In fluences of Crystal-Field and Interlayer Coupling Interactions on Dynamic Phase Diagrams of a Mixed-Spin(3/2,2)Bilayer System∗
- Molecular Dynamics Simulations of the Elastic Anisotropy of Pd at Extreme Conditions∗
- Statistical Properties of a System Consisting of a Superconducting Qubit Coupled to an Optical Field Inside a Transmission Line
- Thermodynamic Nonequilibrium Features in Binary Diffusion∗
- Spontaneous Emission Originating from Atomic BEC Interacting with a Single-Mode Quantized Field
- Thermal Conductivity of Complex Plasmas Using Novel Evan-Gillan Approach
