Bifurcations and Dynamics of Traveling Wave Solutions to a Fujimoto-Watanabe Equation∗

Li-Juan Shi(师利娟)and Zhen-Shu Wen(温振庶)

School of Mathematical Sciences,Huaqiao University,Quanzhou 362021,China

1 Introduction

The Fujimoto-Watanabe equation

was first discovered by Fujimoto and Watanabe[1]in the classification of third-order polynomial evolution equations of uniform rank with non-constant separants,which admit generalized symmetries[2](non-trivial Lie-Backlund algebras[3]).Sakovich[4]showed that Eq.(1)can be connected with the famous KdV equation.As the advent of Eq.(1),its solutions received considerate attention.In 2010,by using an irrational equation method,Du[5]obtained some implicit expressions of traveling wave solutions to Eq.(1).Further,in 2010,Liu[6]gave the classi fications of traveling wave solutions of Eq.(1)through the method of complete discrimination system.However,it is not so clear that what types of the traveling wave solutions are.In addition,are there other types of traveling wave solutions besides the solutions obtained in Refs.[5–6]?What is more,how about the explicit expressions of traveling wave solutions to Eq.(1)?Driven by these motivations,in this paper,we study the dynamics of traveling wave solutions to Eq.(1)from the perspective of the theory of dynamical systems.[7−12]Based on the method of dynamical systems,we present all possible bifurcations of phase portraits in different regions of the parametric space,through which,we show the sufficient conditions to guarantee the existence of traveling wave solutions including solitary wave solutions,periodic wave solutions,compactons and kink-like and antikink-like wave solutions.Moreover,the expressions of solitary wave solutions and periodic wave solutions are implicitly given,while the expressions of kink-like and antikink-like wave solutions are explicitly shown.

2 Bifurcations of Phase Portraits

In this section,we present the bifurcations of phase portraits corresponding to Eq.(1).

Substitutingu(x,t)=φ(ξ)withξ=x−ctinto Eq.(1),it follows,

where the prime stands for the derivative with respect toξ.

Integrating straightforwardly Eq.(2),we get

wheregis the integral constant.

Lettingy=φ′,we obtain a three-parameter planar system

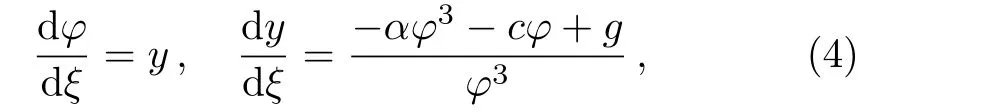
with first integral

Transformed by dξ=φ3dτ,system(4)becomes a regular system

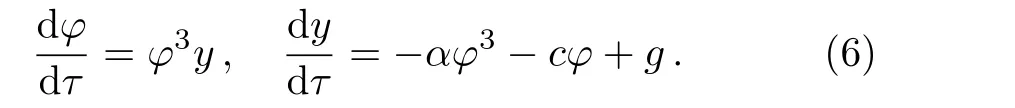
System(6)has the same level curves as system(4).Therefore,we can analyze the phase portraits of system(4)from those of system(6).

To study the singular points and their properties of system(6),let

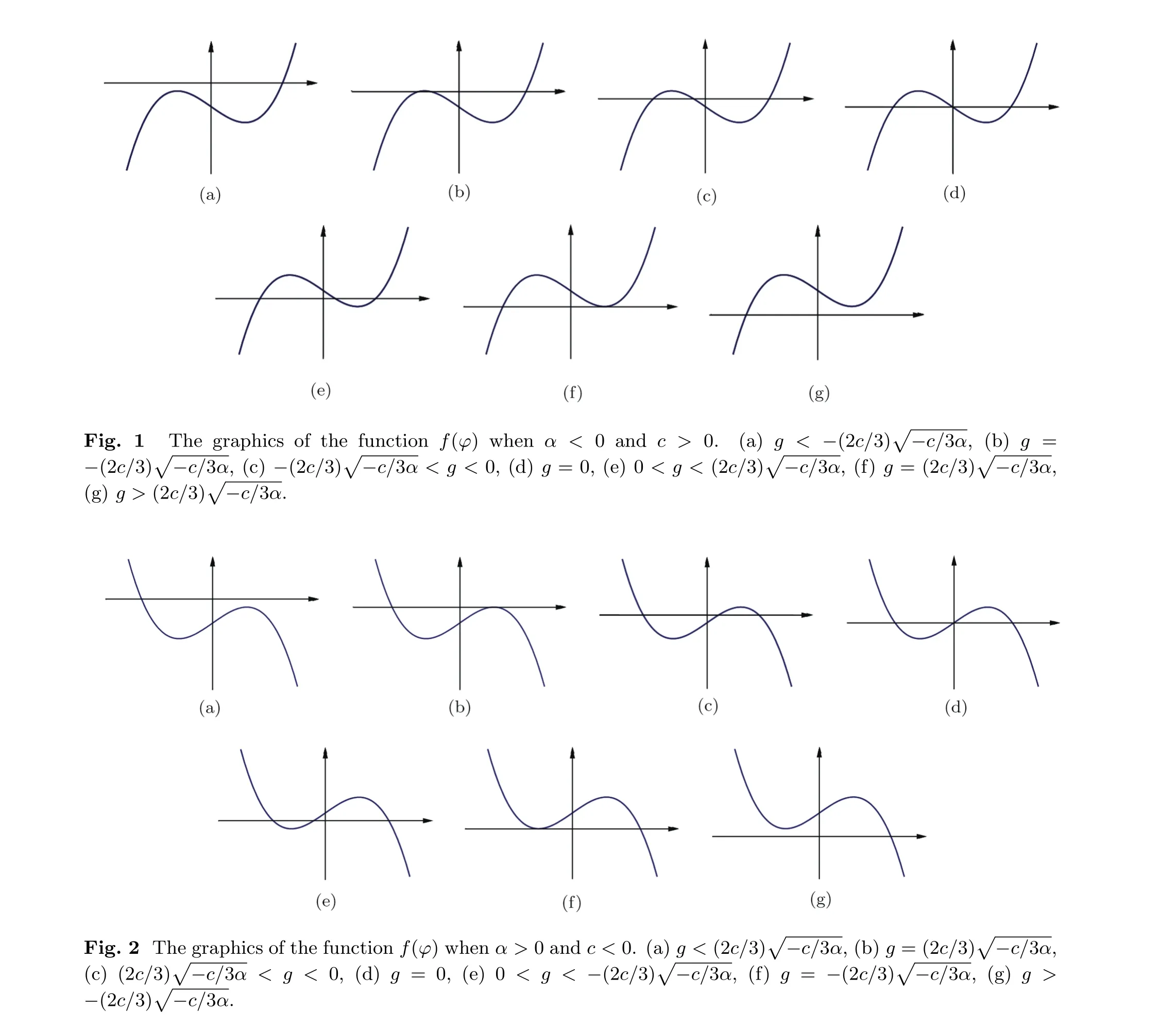
We can easily obtain the graphics of the functionf(φ)in Figs.1 and 2 under corresponding parameters conditions.[13]

Letλ(φ∗,y)be the characteristic value of the linearized system of system(6)at the singular point(φ∗,y).We have

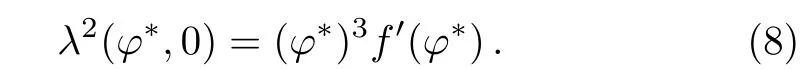
From Eq.(8),we see that the sign off′(φ∗)and the relative position of the singular point(φ∗,0)with respect to the singular linel:φ=0 can determine the dynamical properties(saddle,center,and degenerate singular point)of the singular point(φ∗,0)according to the theory of planar dynamical systems.

We summarize the number,relative positions and dynamical properties of singular points of system(6)whenα<0 andc>0 in the following lemma.Here we just omit these informations for the other case whenα>0 andc<0 for convenience.

LemmaWhenα<0 andc>0,system(6)possesses the following properties.

ProofThe lemma follows easily from Fig.1 and Eq.(8).Note that wheng=0,(φ2,0)is a higher-order singular point with no orbit entering according to Ref.[14]. ?Therefore,based on the above analysis,we obtain all possible phase portraits of bifurcations of system(4)in Figs.3 and 4.

3 Main Results and the Theoretic Derivations of Main Results

To state conveniently,we introduce some marks,

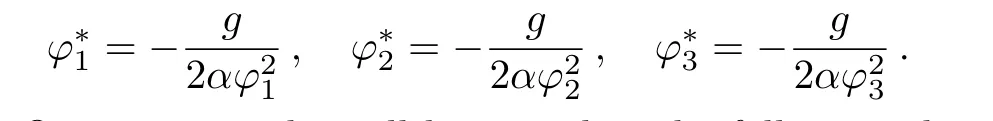
Our main results will be stated in the following theorem,and the proof follows.Note that we only focus our attention on the case whenα<0 andc>0 about the main results,because the other case whenα>0 andc<0 can be considered similarly.

TheoremWhenα<0 andc>0,Eq.(1)possesses the following traveling wave solutions under corresponding parameter conditions.

Wheng=0,there exists a family of periodic wave solutions to Eq.(1),

Substituting Eq.(15)into dφ/dξ=yand integrating them along the homoclinic orbit,it follows that

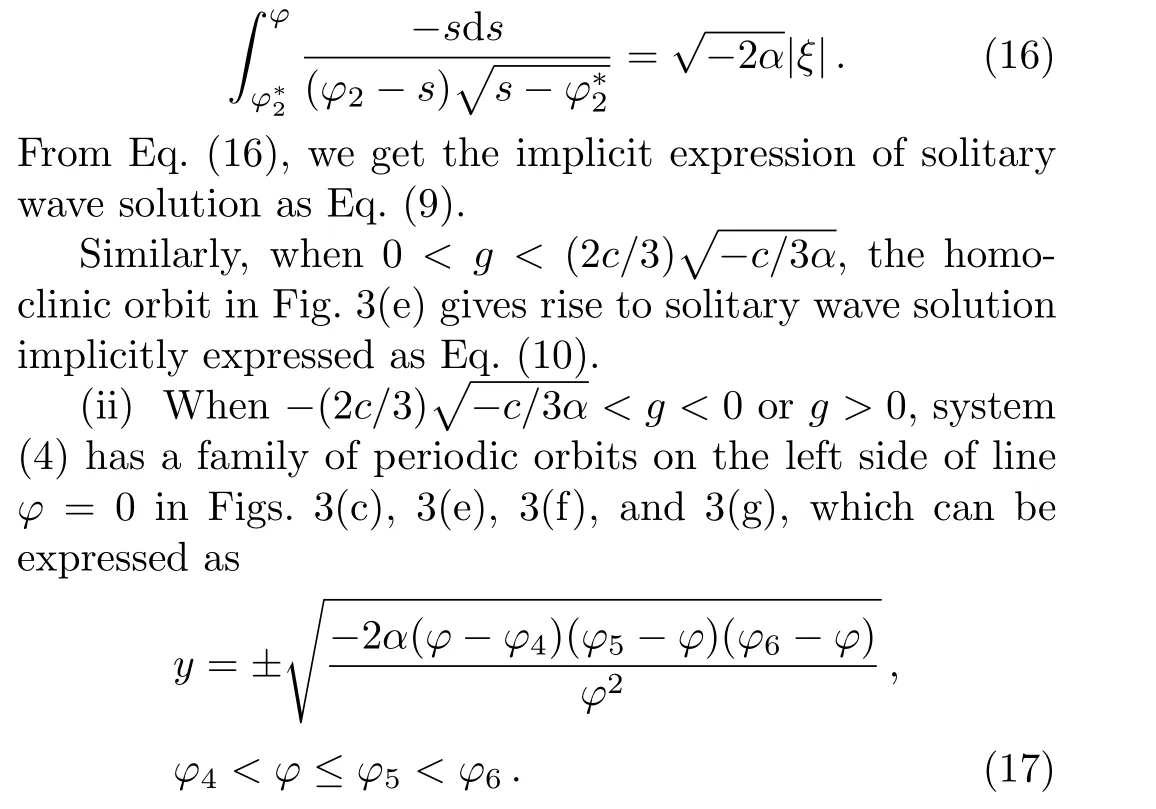
Substituting Eq.(17)into dφ/dξ=yand integrating them along the orbit,it follows that

From Eq.(18),we get the family of periodic wave solutions as Eq.(11).

Wheng=0,the family of periodic orbits in Fig.3(d)can be expressed as from which,we get the family of periodic wave solutions as Eq.(13).

Corresponding to the three family of orbits,passing through the point(φ0,0)with

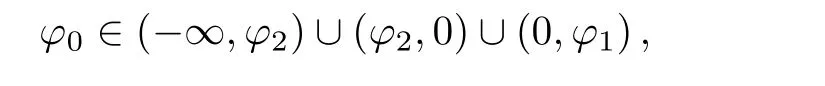
Corresponding to the stable and unstable manifolds defined byH1(φ,y)=H(φ1,0)to the left side of the sad-

(iv) We illustrate the two pairs of kink-like and dle point(φ1,0)andH2(φ,y)=H(φ2,0)to the right side of the saddle point(φ2,0)in Fig.3(c),Eq.(1)has two pairs of kink-like and antikink-like wave solutions shown in Figs.5(b)and 5(c),respectively.

The orbit,which passes the degenerate singuar point(φ1,0)can be expressed as

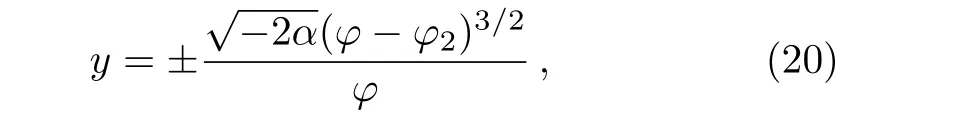
from which,we get the kink-like and antikink-like wave solutions as(14).

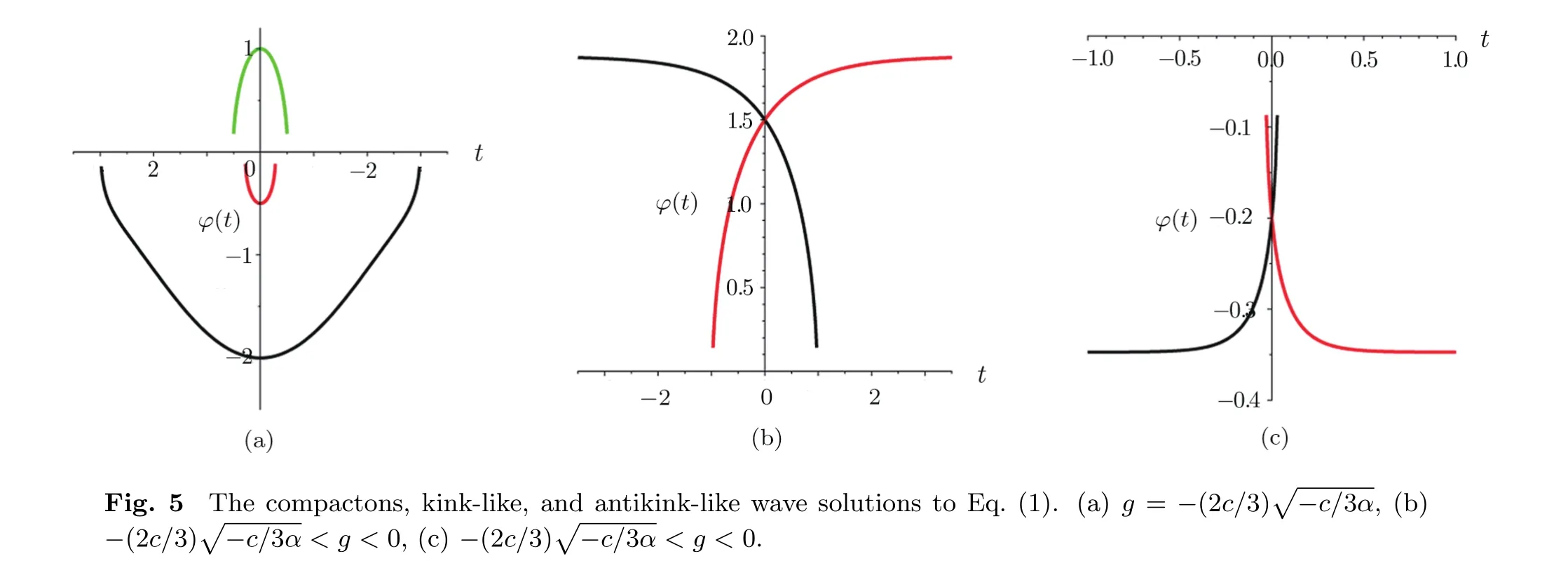
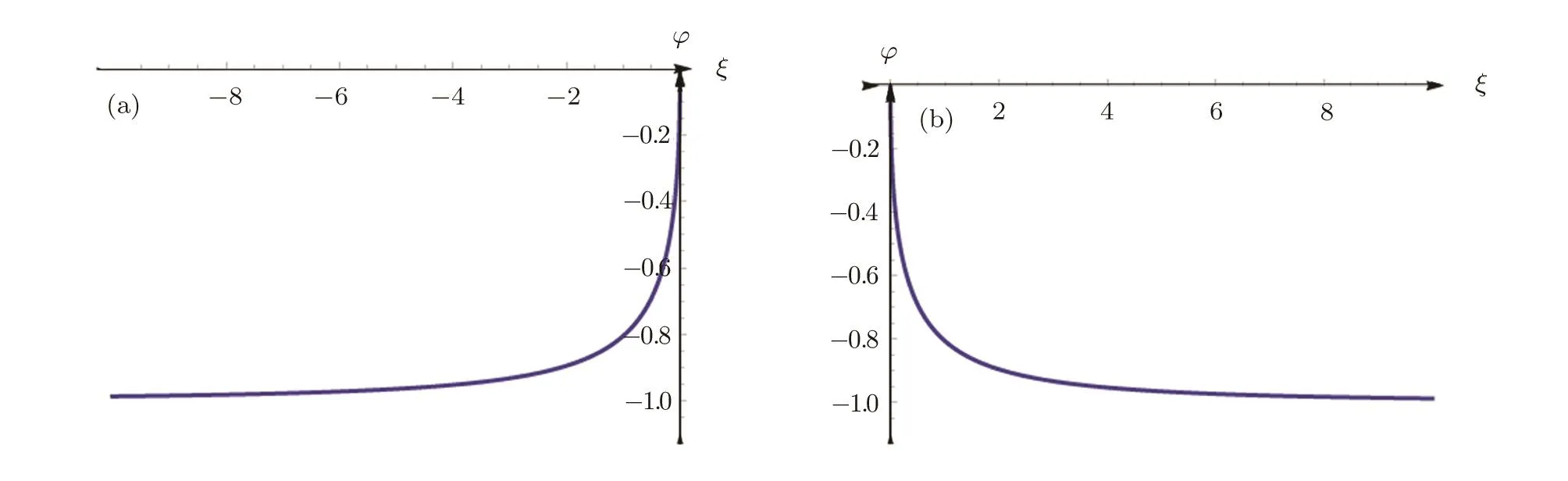
Fig.6 The graphics of the kink-like and antikink-like wave solutions Eq.(14).(a)Kink-like wave solution,(b)Antikink-like wave solution.

4 Conclusions

In this paper,through all possible bifurcations for the system under different parameters conditions,we show the existence and dymanics of traveling wave solutions including solitary wave solutions,periodic wave solutions,compactons and kink-like and antikink-like wave solutions.Moreover,the expressions of solitary wave solutions and periodic wave solutions are implicitly given,while the expressions of kink-like and antikink-like wave solutions are explicitly shown.The dynamics of these new traveling wave solutions will greatly enrich the previews results and further help us understand the physical structures and analyze the propagation of the nonlinear wave.

[1]A.Fujimoto and Y.Watanabe,Phys.Lett.A 136(1989)294.

[2]P.Olver,Applications of Lie Groups to Differential Equations,Springer Science&Business Media,New York(2000).

[3]N.Ibragimov,Transformation Groups Applied to Mathematical Physics,Vol.3,Springer Science&Business Media,Dordrecht(1985).

[4]S.Sakovich,J.Phys.A:Math.Gen.24(1991)L519.

[5]X.Du,J.Phys.75(2010)415.

[6]C.Liu,Comput.Phys.Commun.181(2010)317.

[7]J.Li,Singular Nonlinear Travelling Wave Equations:Bifurcations and Exact Solutions,Science Press,Beijing(2013).

[8]Z.Wen,Nonlinear Dyn.77(2014)247.

[9]Z.Wen,Math.Meth.Appl.Sci.38(2015)2363.

[10]A.Chen,S.Wen,S.Tang,et al.,Stud.Appl.Math.134(2015)24.

[11]Z.Wen,Nonlinear Dyn.87(2017)1917.

[12]Z.Wen,Int.J.Bifurcat.Chaos 27(2017)1750114.

[13]Z.Wen,Z.Liu,and M.Song,Appl.Math.Comput.215(2009)2349.

[14]C.Hu and Y.Lu,J.Beijing Inst.Technol.2(1981)1.