巫山县农村居民点分布与地形因子关系

2018-06-15林孝松崔梦瑞彭孟竹

水土保持研究 2018年4期

徐州, 林孝松, 余情, 崔梦瑞, 彭孟竹

(1.重庆交通大学建筑与城市规划学院, 重庆 400074; 2.重庆交通大学土木工程学院, 重庆 400074)

农村居民点是农村人类社会和自然环境关系的表现核心，其空间分布可综合反映一定自然经济条件下乡村劳动者的生活生产活动状况[1-4]。长期以来，由于缺乏科学的布局规划和统一的规划管理，农村居民点无序建设普遍存在，农村土地资源大量消耗。地貌是地理环境中最重要的组成部分之一，对山区居民点分布具有深刻的影响，尤其是对区位、交通、水源处于劣势的农村居民点的布局起到关键作用[5-6]。因此，研究农村居民点空间分布特征与地形因子关系，对于指导农村居民点统筹规划，促进农村土地集约利用具有重要意义。近年来，随着数字高程模型数据的广泛应用，越来越多的学者引用地形地貌来分析地形与居民点布局的关系[7-15]。姚梦圆[16]、马帅[17]、张霞[18]等引入地形因子分别探索了大别山区、太行山区和喀斯特槽谷地区农村住房空间分布格局及地形要素的影响。

以重庆市巫山县为研究区，选取高程、坡度、坡向、地形起伏度、坡度变率和高程变异系数6个地形因子，利用GIS空间分析功能，基于分布指数、信息熵和变维分形理论方法，综合分析巫山县乡村聚落空间分布格局和地形因子之间的关系，揭示其分布规律及地形地貌对农村居民点布局的影响，研究成果可为巫山县农村居民点规划建设和农村土地整理提供参考。

1 研究区概况及数据来源

1.1 研究区概况

巫山县位于重庆市东北部，位于109°33′—110°11′E，30°45′—23°28′N；幅员面积2 958 km2，辖25个乡镇(街道)，340个村(居委会)；境内深谷和中低山交错分布，坡度大，大巴山、巫山、七曜山三大山脉交集县境，最高海拔2 683 m，最低海拔76 m，属中低山区；巫山县属于亚热带季风性湿润气候，垂直差异明显，具有典型的立体气候特色，年均气温约18.4℃，年平均降水量1 041 mm；2016年末，巫山县农业人口28.08万人，非农业人口17.47万人，人均GDP为22 182元。

1.2 数据来源及处理

研究数据主要有2015年巫山县1∶1万土地利用现状图，从中提取到巫山县详细的农村居民点斑块；巫山县1∶5万DEM数据，从中提取研究区高程与坡度等地形因子信息；2015年巫山县行政区划图。

基于巫山县DEM数据，选取高程、坡度、坡向、地形起伏度、坡度变率和地形高程变异系数6个地形因子作为分析指标；按照研究区自然环境状况，利用ArcGIS将各地形因子划分为9个等级，对各地形因子进行分级显示(附图4)。

2 研究方法

2.1 分布指数法

农村居民点面积比重和不同地形梯度区段的面积差异容易影响农村居民点的分布概率。引入分布指数(Pe)可消除面积差异量纲，并描述农村居民点在不同地形条件下的分布状况。其计算公式为[19]：

(1)

式中：Sie表示i地形因子上第e级地形位农村居民点的分布面积；Si表示i地形因子上农村居民点的总面积；Se表示某特定地形因子第e种地形位的土地面积；S表示巫山县的土地总面积。

如果Pe大于1，表明农村居民点在第e级地形位上的分布属于优势分布，即该地形位对农村居民点分布占主导地位。Pe值越大，优势程度越大。

2.2 信息熵法

信息熵可量度系统内部组态信息的缺乏程度，引入信息熵(He)可反映巫山县农村居民点分布结构特征的有序性。假定巫山县农村居民点在每种地形位上的分布都为一个系统，那么此系统越有序，信息熵就越低，即在此地形位上有序程度越高。其计算公式为[3]：

(2)

式中：Sie代表i地形因子上第e级地形位农村居民点的分布面积；Si代表巫山县农村居民点总面积。农村居民点分布的有序程度随着He熵值的减小而增大，反之亦然。

2.3 变维分形法

对于任一分形维数D在双对数坐标下分形的非线性问题可通过变维分形将其转化为常维分形的形式[20-22]。可引入变维分形探究巫山县农村居民点空间分布与地形因子间的关系。其表达式为：

D=F(r)

(3)

以研究区某地形因子某地形位上农村居民点的分布数目为N(r)，以地形位的分级为r，进行1阶或多阶的累积和系列变换，直到将其转换为常维分形形式。累积和的系列变换过程如下：

(1) 若原始数据点对为(Ni，ri)，则有基本序列：

Ni=N1,N2,N3,…

(4)

根据基本序列构造，进行一次累积和得到序列S1，即：

S1i=S11,S12,…,S1n

=N1,N1+N2,N1+N2+N3,…

(5)

式中：S11=N1，S12=N1+N2，S1n=N1+N2+…+Nn，i=1，2,…,n。

(2) 以此类推，重复第1步，可得二阶、三阶、…、n阶累计和序列，S3，…，Sn，即：

S2i=S11,S11+S12,S11+S12+S13,…
S3i=S21,S21+S22,S21+S22+S23,…
…
Sni=S(n-1)1,S(n-1)1+S(n-1)2,S(n-1)1+S(n-1)2+S(n-1)3,…

(6)

(3) 将数据点对(Sni，ri)标注于双对数坐标，选择拟合效果良好的变换，计算其常分维数。累积和阶数越高，表明农村居民点在相应地形因子上的变维分形特征越复杂，居民点分布与相应地形因子的敏感度越低；相同累积和阶数下分维值越大，表明相应地形因子对农村居民点分布的影响程度越强。

3 结果与分析

3.1 巫山县地形因子及农村居民点分布特征

根据研究区地形特点对各地形因子进行重分类，并借助GIS空间分析功能，统计得到巫山县农村居民点在不同地形因子梯度上的分布情况(表1)。

由表1可知，巫山县地形因子各地形位分布具有相对集中特性，以较低级别地形位为主。高程方面主要集中于250～1 500 m的5个梯度区间，占总面积的78.72%；多数坡度集中在15°～35°的4个梯度区间，占比为58.34%；坡向方面，除平地外，各坡向间面积占比差异较小，以北坡和南坡占比较大，分别为16.33%和15.80%；15～60 m地形起伏度区间占总面积的76.46%；坡度变率以3°～15°系数值间区域为主，占比为69.11%；高程变异系数以0～0.02区间为主，占比为75.32%。

研究区农村居民点分布具有相对集中于较低级别地形位区间，且随地形位级别增高而不断减少的总体特征。如农村居民点在高程方面集中分布于250～1 250 m，占居民点总面积的83.68%，从1 000 m高程开始，居民点分布面积随高程增加而递减；在坡度方面，农村居民点集中分布于15°～35°的区间，占比为86.32%，从25°坡度开始，农村居民点面积随坡度增加而减少；在坡向方面，除平地外，各坡向农村居民点面积占比差异不明显，偏南方向农村居民点占比较大，分布在南、西南、东南3个坡向的农村居民点面积占比41.12%；在地形起伏度方面，农村居民点集中分布较明显，集中化指数高达0.900 5，45 m以下区间占比高达91.08%且15～30 m区间占比达48.74%；坡度变率方面，居民点集中在系数0°～12°的4个梯度区间，占比为78.58%；高程变异系数方面，居民点集中分布在系数值为0～0.02的区间，总面积为74.34 km2，占比达83.21%。总体来看，巫山县农村居民点分布与中低级别地形位间关系较大，但坡向的影响不显著。

表1 地形因子及农村居民点分布面积统计

3.2 地形因子与农村居民点分布格局的关系

利用公式(1)—(2)计算得到各地形因子不同级别地形位农村居民点的分布指数和信息熵值，在此基础上绘制得到巫山县农村居民点地形因子分布指数和信息熵图(图1)，由此可分析农村居民点在不同地形因子上分布的优势地形位及其有序程度。

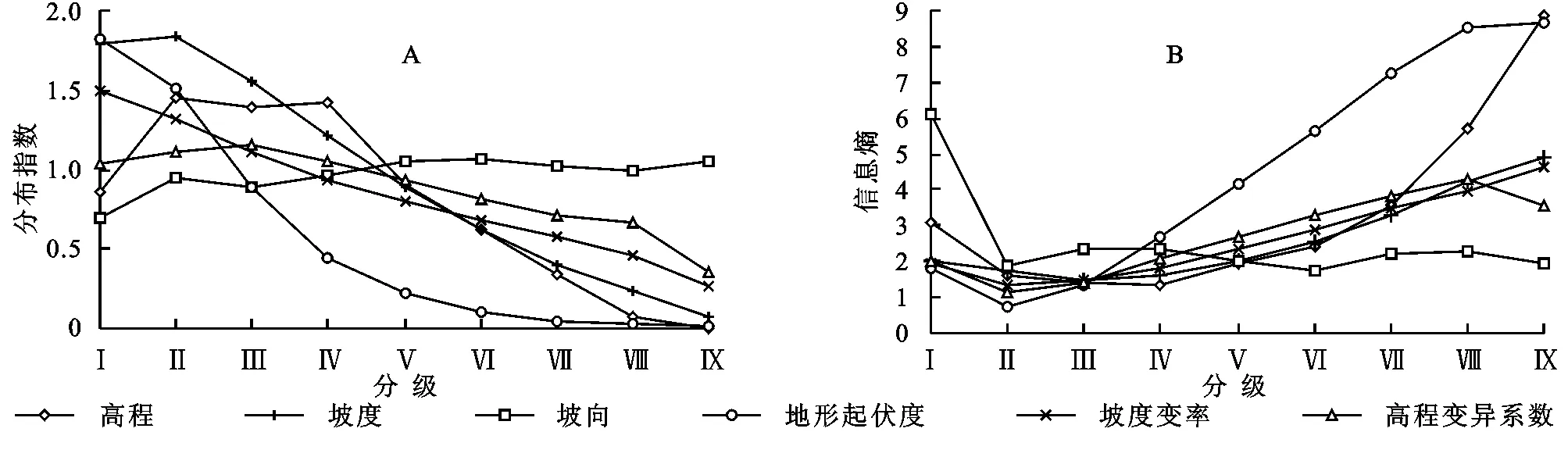
图1农村居民点地形因子分布指数及信息熵

3.2.1 农村居民点分布的优势地形位农村居民点各地形因子分布指数曲线在一定程度上反映了农村居民点在各地形位梯度上的优势分布特征。由图1A可知，除坡向外，农村居民点在各地形因子上的分布指数均呈现出不同程度下降的总体趋势。

农村居民点在坡度和地形起伏度等地形位上的分布指数值随级别升高下降幅度最大。其中，农村居民点在坡度上的分布指数峰值出现在10°～15°(Ⅱ级)区间，当坡度大于25°时，分布指数小于1并持续减小，这说明巫山县农村居民点在坡度小于25°的地形位区间具有分布优势，且集中于10°～15°区间，原因在于坡度相对平缓的地区对房屋建筑施工及基础设施布局有利；在地形起伏度上，分布指数值随地形位级别增大而急剧减小，分布指数在0～15 m区间最大为1.82。地形起伏度小于30 m占全县41.46%的区域分布着65.5%的农村居民点，这说明，研究区农村居民点分布的优势地形位为起伏度较小的Ⅰ—Ⅲ级。

农村居民点在坡度变率和高程变异系数上的分布指数曲线下降趋势相对较缓。在坡度变率上，分布指数单调递减，在坡度变率小于9°的3个梯度上分布指数均大于1，为研究区农村居民点分布的优势地形位。这是因为随着坡度变率的增大，不利于农业生产和民宅建筑的施工，从而导致农村居民点数量的减少；在高程变异系数上，分布指数呈现出随地形位级别增加而先增加后减少的规律。在高程变异系数小于0.02的4个区间内，分布指数均大于1，这是因为地形的垂直变化较小，土壤侵蚀强度小，农作物耕种条件好，适合农村居民点布局。

农村居民点在高程上的分布指数曲线呈倒U字型，即先增大后减小。分布指数在高程250～500 m，500～750 m和750～1 000 m的值分别为1.45，1.39，1.42，均大于1，说明该区间为农村居民点分布的优势地形位。当高程大于1 000 m时，农村居民点的分布指数小于1并持续减小，原因在于随着海拔的增加气温降低，再加上山地地形的限制，适宜农业生产的土地大量减少，导致农业人口聚居条件变差，居民点数量相应减少。

农村居民点在坡向上的分布指数上下波动，变化幅度较小。在东南、南、西南、西北方向分布指数大于1，说明这4个坡向为研究区农村居民点分布的优势地形位。由于巫山县地处中国西南，良好的通风、采光条件是择宅的关键，而东南、南、西南坡均属于阳坡半阳坡，日照时数长，光照条件好。

3.2.2 农村居民点分布的有序度农村居民点各地形因子信息熵变化曲线在一定程度上反映了农村居民点在各地形位级别上的有序性特征。由图1A可知，农村居民点在各地形因子上的信息熵曲线在前两级地形位上均有所下降，之后呈现出不同程度的总体上升趋势。

农村居民点在高程与地形起伏度上的信息熵值上升幅度最大。在高程上，农村居民点的信息熵谷值出现于500～750 m区间，即在该区间居民点分布最有序，这与该地形位的优势分布高度关联。原因在于巫山县农村居民点普遍依山而建，在高程小于500 m的区域中所占比例相对较低，因此较低海拔区域成为农村居民点分布最有序的地带；在地形起伏度上，农村居民点信息熵值先递减后递增，最小值出现在15～30 m区间，值为0.72。由于巫山县起伏度小于15 m的区域大多已开发为城市建设用地，区域内的农村居民点分布零碎散乱，面临被拆迁改造的现实，信息熵和无序度较高。城区周边地形起伏度在15～30 m的区域地势较平坦，适宜进行乡村规划建设，因此起伏度为15～30 m的低海拔缓坡地区农村居民点分布最有序。

农村居民点在坡度、坡度变率和高程变异系数上的信息熵值上升趋势相对较缓。在坡度上，信息熵值先减少后增加，信息熵最小值出现在15°～20°区间。最低坡度梯度的区域上，农村居民点分布有序程度并非最高，这是因为大部分坡度为0°～10°的区域为城镇建设用地，坡度为10°～15°的城区周边地带的农村居民点较分散且无序，相反15°～20°的耕地集中分布地带农村居民点有序度较高；在坡度变率上，信息熵值总体上先减后增，最小值在3°～6°区间，值为1.35，说明在坡度变率变化较小的区域，农村居民点分布的有序程度较高，且和其优势地形位高度关联；在高程变异系数上，信息熵在0.005～0.01，0.01～0.015两个区间较小，分别为1.12，1.41，这与农村居民分布的优势地形位相一致，在高程变化较小的区域，农村居民点的布局越有序。

农村居民点在坡向上的分布指数值先减小，后上下波动，与其分布指数曲线类似。平地上居民点分布的信息熵最大，这是由于仅有的平地多被城市建设用地所占，导致少许零星居民点无规则地散布在平地区域，有序度最低。同时，坡向上的农村居民点分布信息熵曲线波动幅度较小，且熵值也较小，反映出巫山县农村居民点顺坡而建现象普遍，各坡向上居民点布局都比较有序。

3.3 地形因子与农村居民点的变维分形特征

基于ArcGIS平台，统计得到巫山县农村居民点在不同地形因子梯度上的斑块数目(表1)，在此基础上，通过累积和的系列变换，计算得到巫山县农村居民点与各地形因子的分段变维结果(表2)以及巫山县农村居民点在不同地形因子各地形位梯度上的分段变维序列图(图2)。

由表2和图2可知，经过1阶或多阶累积和变维分形变换后，巫山县6个地形因子的分段变维拟合函数的相关系数均达到0.97以上，数据点序列呈现良好的线性关系。各地形因子对应的累积和变换次数和分维值存在一定的差异，表明巫山县各地形因子与农村居民点分布之间的敏感性及影响程度有较明显差别。

表2 农村居民点与地形因子的分段变维特征汇总

图2 农村居民点分布与各地形因子的分段变维序列

巫山县农村居民点的分布与坡度呈一阶累积和分形分布，表明坡度与农村居民点的分段变维分形特征较为简单，农村居民点的分布对坡度的敏感性最高，是研究区内农村居民点分布的主要影响因素；巫山县农村居民点分布与高程、坡度变率、地形起伏度和高程变异系数之间均呈二阶累积和变维分形分布，表明这些因子与农村居民点的分段变维分形特征较复杂。在累积和变换次数为2的地形因子中，高程的分维值最大，表明其对农村居民点空间格局的形成和发展影响程度最高，坡度变率和地形起伏度次之，高程变异系数最低；农村居民点与坡向之间呈三阶累计和变维分形分布特征，表明农村居民点的分布对坡向的敏感性最低，这与居民点在坡向上的分布指数曲线与信息熵曲线呈现上下小幅波动的趋势相吻合，表明坡向对巫山县农村居民点分布的影响程度相对较弱。综上可知，各地形因子对巫山县农村居民点分布和发展的影响程度由高到低分别是坡度>高程>坡度变率>地形起伏度>高程变异系数>坡向。

4 讨论与结论

(1) 农村居民点的空间分布充分体现了乡村聚落和自然环境的关系，是对地形地貌长期选择适应的结果。巫山县农村居民点的空间分布在不同地形因子不同地形位梯度上，具有不同的布局特征。农村居民点分布的优势地形位为高程250～1 000 m，坡度0°～25°，东南、南、西南和西北坡向，地形起伏度小于30 m，坡度变率为0°～9°，高程变异系数0～0.02；同时，农村居民点用地规模和有序程度随着海拔、坡度、坡度变率、地形起伏度、高程变异系数地形位的增加而呈现不断减少趋势。

(2) 变维分形值能够定量揭示各地形因子与农村居民点分布之间的敏感关系。研究区6种地形因子与农村居民点分布均呈现出分段变维分形特征，表明这些地形因子在一定程度上影响了农村居民点的分布。研究区农村居民点与坡度呈一阶累积和分形分布，表明其对坡度的敏感性最高；与高程、地形起伏度、坡度变率和高程变异系数均呈二阶累积和分形分布；与坡向则呈三阶累积和分形分布，表明其对坡向的敏感性最低；地形因子对研究区农村居民点分布的影响程度由高到低分别为坡度>高程>坡度变率>地形起伏度>高程变异系数>坡向。

研究结果体现了渝东北典型山区农村居民点分布与地形因子的相互关系，也在一定程度上反映了农村居民点规划建设的局限性。此外还发现巫山县在高程大于2 000 m、坡度大于45°的局部区域依然有部分乡村聚落分布，这说明研究区内农村居民点格局还需进一步优化。此外，本研究仅从单一多指标的地形因子综合分析了巫山县农村居民点的分布格局，今后需进一步结合社会经济因素和生产条件因素等多指标，综合研究巫山县农村居民点的分布格局和演化规律。

参考文献:

[1] 李姗姗,曹广超,赵鹏飞.秦巴山区农村居民点空间分布及其影响因素分析:以陕西省宁强县为例[J].水土保持研究,2014,21(3):186-191.

[2] 李君,李小健.综合区域环境影响下的农村居民点空间分布变化及影响因素分析:以河南巩义市为例[J].资源科学,2009,31(7):1195-1204.

[3] 焦贝贝,石培基,刘春芳,等.黄土高原低山丘陵区农村居民点分布与地形因子关系研究:以兰州七里河区为例[J].资源科学,2013,35(8):1721-1723.

[4] 张颖,徐辉.基于MCR模型的农村居民点布局适宜性分区及优化模式研究:以南京市六合区金牛湖街道为例[J].长江流域资源与环境,2014,23(11):1485-1492.

[5] 闫庆武,谭学玲.基于GIS的半干旱农牧交错区农村居民点分布特征研究:以内蒙古伊金霍洛旗为例[J].干旱区资源与环境,2017,31(5):107-109.

[6] 钟克强,李爱迪,武伟,等.西南山区地形因子对农村零散居民点分布的影响[J].湖南农业科学,2017(2):107-113.

[7] 闵婕.基于村域的农村居民点空间格局及影响因素分析:以石柱县冷水镇八龙村为例[J].水土保持研究,2014,21(1):157-162.

[8] 刘耀林,范建彬,孔雪松,等.基于生产生活可达性的农村居民点整治分区及模式[J].农业工程学报,2015,31(15):247-254.

[9] 王重玲,朱志玲,白林波,等.宁夏中部干旱带农村居民点空间分布研究[J].中国农学通报,2015,31(10):269-277.

[10] 谭雪兰,周国华,朱苏晖,等.长沙市农村居民点景观格局变化及地域分异特征研究[J].地理科学,2015,35(2):204-210.

[11] 樊天相,杨庆媛,何建,等.重庆丘陵地区农村居民点空间布局优化:以长寿区海棠镇为例[J].地理研究,2015,34(5):883-894.