Dynamic Mechanical Characteristics and Damage Evolution Model of Granite
2018-06-15ShuaifengWuYingqiWeiHongCaiBeiJiaandDianshuLiuChinaInstituteofWaterResourcesandHydropowerResearchBeijing00038ChinaSchoolofMechanicsandCivilEngineeringChinaUniversityofMiningandTechnologyBeijing00083China
Shuaifeng Wu, Yingqi Wei Hong Cai Bei Jia and Dianshu Liu(.China Institute of Water Resources and Hydropower Research, Beijing 00038, China; .School of Mechanics and Civil Engineering, China University of Mining and Technology, Beijing 00083, China)
In the field of rock engineering, blasting is widely used as an economical and effective method and in this case the rock is subjected to dynamic loading. A large number of engineering practices and theoretical researches show that[1-4]the mechanical properties of rock under dynamic loading and static loading are significantly different; at the same time, when rock mass is blasted, the stress wave generated by one blasting cannot cause the direct failure of rock mass, but multiple stress waves will make the instability or damage of the rock mass, which exhibits the cumulative damage effect.
The impact mechanical property of rock is an important basic aspect of rock dynamics, and constitutive curves and failure characteristics of the rock under dynamic loading are mainly got by a split Hopkinson pressure bar (SHPB) device and a light gas gun experimentally. Mao Xianbiao[5]conducted static and dynamic contrast tests of red sandstone then got the staged characteristics of stress-strain curve under static and dynamic loadings and pointed out that after the strain rate was greater than 66 s-1, the sandstone showed strain softening characteristics. Li Xibing[6]conducted a SHPB test on sandstone and found that during the strain rate range from 50 s-1to 100 s-1, the dynamic strength of the sandstone was all higher than the static strength, the strength ratio of dynamic and static was between 1.2 and 1.8, and dynamic compressive strength of the sandstone increased with the strain rate increasing, showing a strong strain rate effect. The research on impact mechanical properties of rock are mainly focused on the rock strength characteristics at different strain rates, but hardly considered the wavelength effect, however, in engineering blasting it shall not be ignored that the rock is influenced by the stress wave at various wavelengths.
The research on rock damage evolution under impact uses the method of damage mechanics to describe the mechanical behavior of rock material and the key is the establishment of damage evolution model. Li Xibing[7]obtained the threshold value of damage by using the SHPB to hit the granite specimens cyclically. Based on logistic function as the prototype, Jin Jiefang[8]established the rock damage model which was suitable under the effect of confining pressure and cyclic impacts. In recent years, scholars constructed various types of rock damage models but had little research on the damage evolution under stress wave with different wavelengths and amplitudes.
Based on the above research results, a SHPB device is used to conduct impact loading tests on granite under different wavelengths and amplitudes, and through loading tests under the combination of different lengths and impact velocities of bullet, the research on dynamic mechanical properties and the damage evolution of granite is carried on.
1 SHPB Test Device and Program
The test device was the SHPB system with 75 mm in diameter, a 3.5 m long incident bar, a 3.5 m long transmission bar, 0.30 as the Poisson ratio, 210 GPa as the elastic modulus and 7 850 kg/m3as the density. The measuring frequency of super dynamic strain instrument analyzing the stress wave was 1.2 MHz, and the AF-120 semiconductor strain gauge was used in conjunction in the system. In the SHPB test, the test process should be made to satisfy the one-dimensional wave assumption and stress homogeneity assumption, which requires selecting reasonable-size specimens[9]. Based on the above premises, designing the sample size and selecting the cylinder with 50 mm in diameter, 40 mm in length, surface precisely grinded and uneven flatness controlled within 0.02 mm, and also in order to avoid the interfacial friction effect, the lubricants are applied at both ends of the specimens. Granite is used as the test rock and the specimens whose velocity difference is within 5% are selected after the ultrasonic testing to ensure the consistency. By a frequency method, the properties of the granite were statistically obtained: the longitudinal wave velocity is 5 667 m/s, the elastic modulus is 58 GPa, the uniaxial compressive strength is 98 MPa, and they are homogeneous and compact.
In order to study the dynamic and mechanical properties of granite under different stress wave parameters, the core idea of the test was to get the dynamic response rules of granite with the change of stress wavelengths and amplitudes.The wavelength of stress wave was determined by the length of the bullet, the amplitude was determined by the speed of the bullet, and the test covered four kinds of wavelength respectively to 0.8 m, 1.2 m, 1.6 m and 2.0 m, five-grades classification of bullet speed, a total of 20 groups, and each test was repeated 3 times or more. The range of wavelength was selected mainly considering that not only cover common stress wave that SHPB test provided, but also produce certain differences between the test groups; the impact velocity was selected mainly considering the speed range corresponding to the rock starting from showing dynamic strength slightly larger than static strength to causing comminuted damage.
2 SHPB Test of Granite
2.1 Analysis of strain rate effect of dynamic mechanical properties of granite
The results of impact test are shown in Tab.1.
The impact test is carried out under the assumptions of one-dimensional stress and homogeneity, and the same rule is observed under all wavelengths. The length of impact bar is only 800 mm. The waveform is shown in Fig.1.

Tab.1 Results of SHPB test of granite
From the waveforms in Fig.1, it can be observed that, for the same length of impact bar, the higher the impact velocity is, the bigger the stress amplitudes of the incident wave and transmission wave and reflection wave are, and the velocity and the stress amplitude have a linear relationship, which coincides with the stress wave amplitude formulaσ=ρCV/2, corresponding to the constitutive curve as shown in Fig.2. The dynamic peak strength of granite has a good correlation with the strain rate, and it is positive. With the increase of strain rate, the dynamic elastic modulus also increases.

(1)

Fig.1 Incident and reflection waves at 800 mm wavelength

Fig.2 Constitutive curves at 800 mm wavelength

Fig.3 Relationship between dynamic strength and strain rate
2.2 Analysis of wavelength effect of dynamic mechanical properties of granite
Under the impact, the deformation and the failure state of granite show a strong correlation with the wavelength of stress wave.When the range of strain rate is basically consistent and the wavelength increases from 0.8 m to 2.0 m, the peak strain of granite increases gradually, and the wavelength increases 0.4 m each step, the peak strain is overall uplifted with about 10%. Fig.4 indicates the relationship between peak strain and stress wavelength at different wavelengths under the same strain rate, and the strain rate shows a linear relation within 102s-1. In summary, when the granite is under impacts with different stress wavelengths and amplitudes, the loading strain rate is only related to the impact velocity, and the dynamic strength growth factor and the natural logarithm of the strain rate of granite is a linear relationship within the strain rate of 102s-1; the growth of stress wavelength makes granite being subjected to more energy effects under the same amplitude and the peak strain correspondingly increases, showing a linear relationship on the whole.

Fig.4 Relationship between wavelength and peak strain
3 Evolution Law of Dynamic Damage of Granite
3.1 Impact damage test of granite
In order to study the damage evolution law of granite under the stress wave, the stress wavelength and amplitude are considered as variables, and the effect of multiple impactson cumulative damage are also considered. The same four kinds of wavelengths are used as in Section 1, but the damage evolution is aimed at the rock damage development rather than destruction, therefore, a low impact velocity is selected and it is divided into five levels of speeds, and on the basis of the characteristics of the specimens being susceptible to damage under the impact of large wavelength, the effect of impact time on damage development is studied, while the multiple impacts for 3 times are set uniformly. The damage amount was characterized by the method of acoustic wave measurement, shown as
(2)
3.2 Damage evolution law of granite
In the test, at least three series of parallel tests were conducted under each impact velocity gradient while eliminating the singular data, to reduce the effect of the discreteness and the dynamic-static mechanical parameters were obtained at different wavelengths and impact velocities. The test results of granite under three times of stress wave effect at 0.8 m wavelength with 5 kinds of velocity gradient, are listed in Tab.2.
Strain rate is an index reflecting the rock under dynamic loading, and establishing the relationship between rock dynamic mechanical properties and strain rate can not only reflect the mechanical behavior under loading of specimens itself, but also reflect stress wave parameters. Tab.2 shows that the impact velocity and strain rate of specimens are in a linear relationship. The basic principle of stress wave indicates that the amplitude of impact velocity and stress wave is in a linear correlation, therefore the relationship between amplitude and damage is transformed into the relationship between strain rate and damage.

Tab.2 Damage of granite under three times stress waves effect at 0.8 m wavelength
The damage of granite was gradually increased under three-times stress wave effect, which is called the cumulative damage effect. The relationship between strain rate and cumulative damage was established according to the data of three series of parallel test at 0.8 m wavelength, as shown in Fig.5. The figure shows that the faster the bullet speed, the higher the strain rate and the greater the damage become. The cumulative damage develops slowly at the low strain rate and rapidly at the middle-high strain rate, showing exponential relationship as the whole.

Fig.5 Relationship between strain rate and cumulative damage under three times of impact at 0.8 m wavelength
The wavelength is another factor of the stress wave parameters, and the effect of wavelength changing on damage is also an important part of the damage evolution of granite. The relationship between strain rate and cumulative damage at 4 kinds of different wavelengths in the test was shown in Tab.3, and Fig.6 shows that the relationship between strain rate and damage.

Fig.6 Relationship between strain rate and damage accumulation at different wavelengths
Fig.5 and Fig.6 show that as the strain rate increases, the cumulative damage increases, and the different times of stress waves effect makes the strain rate corresponding to the same cumulative damage being different, and the more the impact times, the lower the strain rate becomes. Meanwhile, at the same wavelength, the cumulative damage in high strain rate intensifies with the increase of impact times, and the cumulative damage is exponentially increasing with the increase of strain rate. In the case of the same strain rate range, the stress wavelength increases, the cumulative damage curve of granite is raised overall, and the cumulative damage is still exponentially increasing with the increase of strain rate.
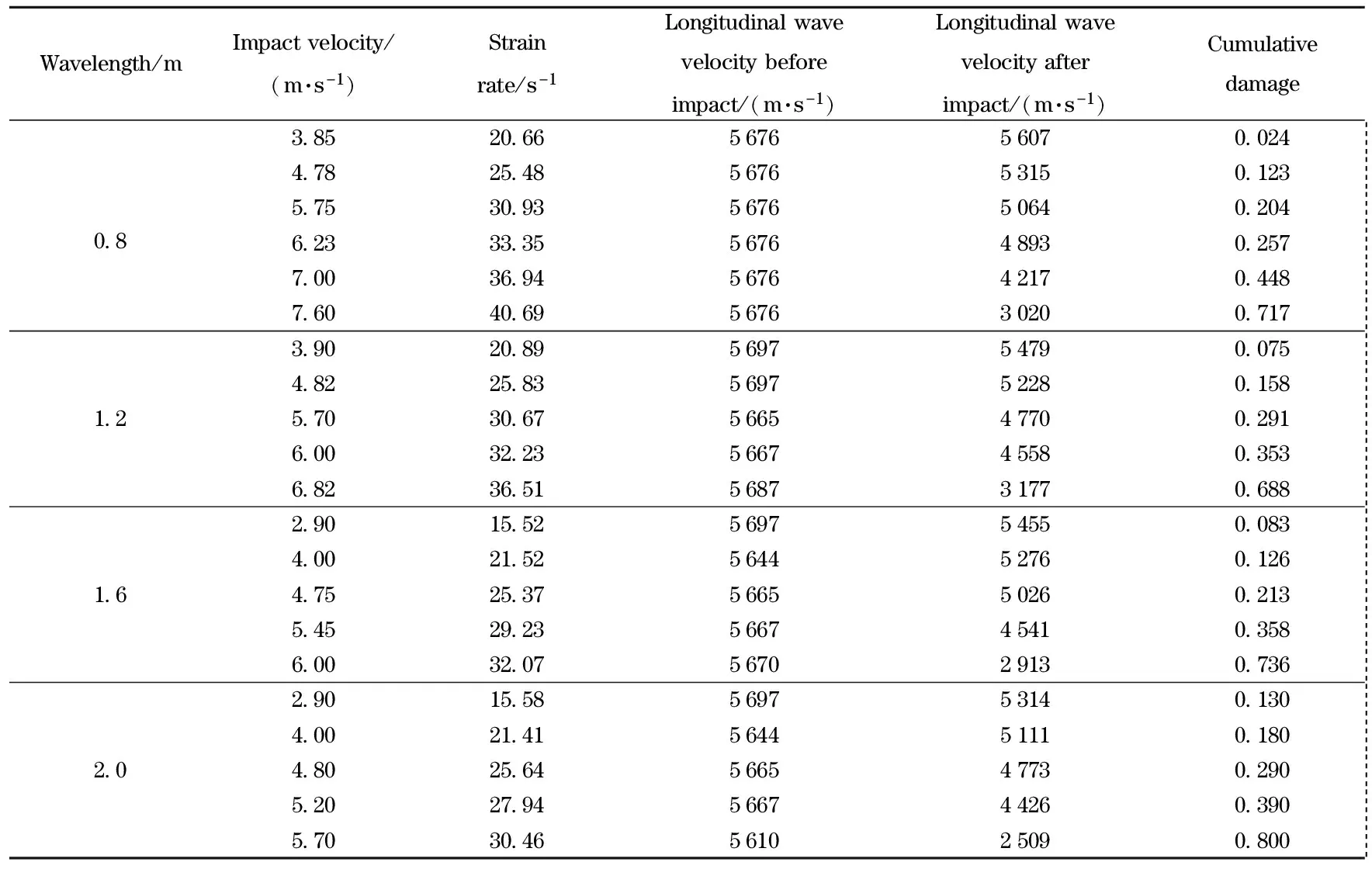
Tab.3 Damage of granite at different stress wavelengths
3.3 Damage evolution model
3.3.1Model construction
The response of rock under loading can be studied by its current mechanical characteristics. In the test, the cumulative damage evolution of granite was studied by changing the impact velocity, wavelength and impact times. At the same time, the development of cumulative damage is influenced by mechanical parameters of rock itself, so the evolution model of cumulative damage will be established as

(3)
D=Aeant(β+λ)
(4)
After combining and reclassifying:
(5)

3.3.2Physical meaning of parameters
In order to study the physical meaning of the parameterAandαin Eq.(5), fixed the value of one parameter and changed the other, and through analyzing the effect of parameter variation on the model curve, the physical meaning of the parameters are determined.
Whenαwas fixed and the value ofAwas taken for 0.02, 0.04, 0.06, 0.08 and 0.10 respectively, the effect on the model curve was shown in Fig.7.

Fig.7 Effect of A on the model curve
Fig.7 shows that when the strain rate is 30 s-1, the cumulative damage values are 0.091, 0.182, 0.273, 0.364 and 0.455 respectively, and the increase amplitude are all for 0.091. The overall shapes of the curves are similar, and the tangent slopes of the curves increased steadily at the whole range of strain rate and the curve is raised overall with the increase ofAvalue. It shows that the development rate of cumulative damage is increasing. According to the effect of stress wavelength on the damage development and Fig.6, the longer the wavelength, the greater the damage caused by the same strain rate becomes, and the damage evolution pattern is as the same as the effect of the change ofAvalues on the model curve. Therefore, the physical meaning ofAis the prophase cumulative damage rate factor affected by the stress wavelength.
WhenAwas fixed andαvalue was taken for 0.05, 0.055, 0.06, 0.065 and 0.07 respectively, the effect on the model curve was shown in Fig.8. It indicates that the curve clusters are overlapped approximately in the case that strain rate is less than 30 s-1, but there are significant differences later. With the increase ofα, the model curve becomes steeper and the slope becomes greater, it shows the cumulative damage rate increases in the late. Therefore the shape of the curve clusters are similar to the cumulative damage trend of the specimens under multiple impacts, the physical meaning ofαis the anaphase cumulative damage rate factor affected by multiple impacts.

Fig.8 Effect of α on the model curve
From the above, the physical meaning ofAis the prophase cumulative damage rate factor affected by the stress wave length and the physical meaning ofαis the anaphase cumulative damage rate factor affected by multiple impacts. Eq.(5) shows that the physical meaning ofAandαreflect the accuracy of the wavelengthλand the impact timen.
3.4 Model validation
According to the test program in the second section of this paper, the cumulative damage development law of granite was obtained. The fitting values of cumulative damage under various test conditions were obtained after using Eq.(5) to fit, as shown in Tab.4.
Tab.4 shows the impact test data and fitting data in the case of 5 kinds of velocity gradients at the 0.8 m wavelength, and the correlation coefficient of the fitting curve under three times of impacts are 0.981, 0.994 and 0.985 respectively; the fitting errors of cumulative damage are all below 10%, and the fitting effect shows good applicability of the cumulative damage model.
Fig.9 shows the test and fitting data under three times of different impact velocities at each wavelength. It can be seen that at each wavelength, the fitting correlation coefficients of the test data are all more than 0.9, and the fitting effect is ideal. The model can reflect the evolution law of cumulative damage of granite by changing the strain rate at different wavelengths.

Tab.4 Test and fitting value of cumulative damage data at 0.8 m wavelength
The prophase damage accumulation of granite changes little in the case of multiple impacts, the three corresponding fitting curves are overlapped approximately in the early; with the increase of strain rate, the multiple impact effect gradually appears, the curves show obviously a different increasing trend in the late, and the cumulative damage increase rate becomes the fastest under the third time of impact. From the vertical perspective, with the increase of wavelength, at the same strain rate level, the prophase cumulative damage becomes more obvious with the increase of impact time and the uplift amplitude of corresponding fitting curve becomes greater with the increase of impact time.
Through the determination of physical meaning of parameters and verification of test, it shows that the damage model in this paper is sufficient in the theoretical basis and definite in the physical meaning,which can reflect the cumulative damage development trend of granite under different stress wave parameters and multiple impacts and fit accurately.
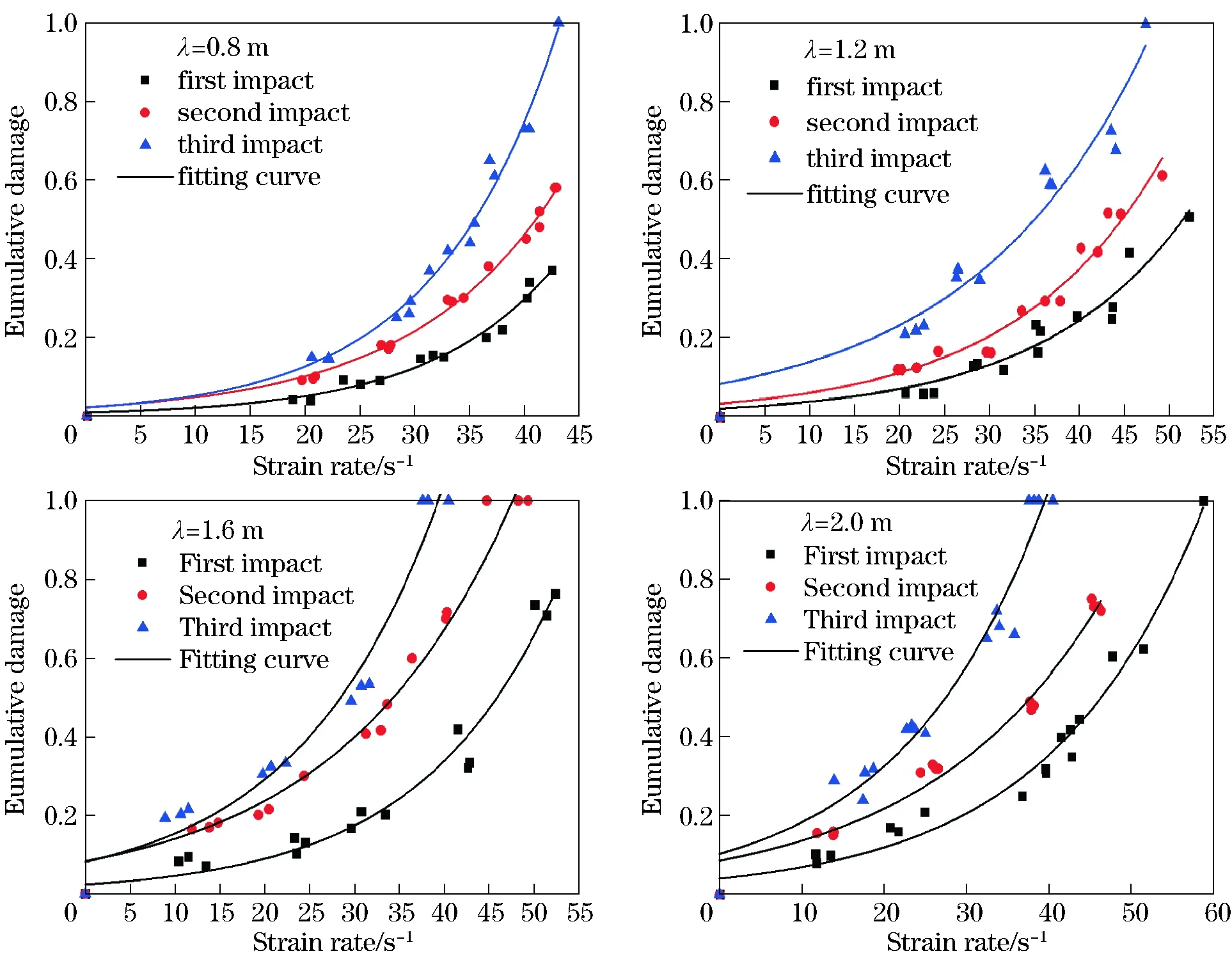
Fig.9 Fitting curves of damage accumulation of granite
4 Conclusions
① Under the effect of impacts at different stress wavelengths and amplitudes, the dynamic compressive strength of granite shows a strong dependence on the strain rate, and the increase factor of dynamic strength and natural logarithm of strain rate show a linear relationship; the peak strain is overall uplifted with the increase of wavelength.
② Under the combined effect of different stress wave parameters and multiple impacts, cumulative damage and strain rate show an exponential increase form; the increase of stress wavelength makes the difference of cumulative damage more obvious at the low strain rate under the effect of multiple impacts, and the increase of impact time makes the cumulative damage development accelerate in the late.
③The cumulative damage evolution model which is established on the basis of exponential function according to the cumulative damage development pattern of granite, can reflect the effect of stress wave parameters and impact time at the same time. The physical meaning of the model parametersAandαare respectively the prophase cumulative damage rate factor affected by the stress wavelength and the anaphase cumulative damage rate factor affected by multiple impacts. The model can reflect that at the same strain rate, the cumulative damage increases with the increase of wavelength; at the same wavelength, the increase rate of cumulative damage increases with the increase of impact time.
[1] Yang Guoliang, Yang Renshu, Che Yulong. Damage accumulative effect of surrounding rock under periodic blasting vibration[J]. Journal of China Coal Society, 2013,38(Supp.1):25-29.
[2] Fu Hongxian, Zhao Yong, Xie Jinshui, et al. Study of blasting vibration test of area near tunnel blating source[J]. Chinese Journal of Rock Mechanics and Engineering, 2011,30(2):335-340. (in Chinese)
[3] Fei Honglu, Zhao Xinpu. Experimental study on cumulative damage in rock slope caused by blasting vibration[J]. Blasting, 2009,26(4):1-4.
[4] Ramulu M, Chakraborty A K, Sitharam T G. Damage assessment of basalticrock mass due to repeated blasting in a railway tunnelling project:a case study [J]. Tunnelling and Underground Space Technology, 2009, 24(2):208-221.
[5] Mao Rongrong, Mao Xianbiao, Zhang Lianying. Experimental research on mechanics properties of red sandstone under dynamic and static loads[J]. Safety in Coal Mines, 2013,44(5):56-59.
[6] Zhu Jingjing, Li Xibing, Gong Fengqiang, et al. Experimental test and damage characteristics of sandstone under uniaxial impact compressive loads[J].Journal of Central South University (Science and Technology), 2012, 43(7):2701-2707.
[7] Li X B,Lok T S,Zhao J. Dynamic characteristics of granite subjected to intermediate loading rate[J]. Rock Mechanics and Rock Engineering, 2005,38(1):21-39.
[8] Jin Jiefang, Li Xibing, Qiu Can, et al. Evolution model for damage accumulation of rock under cyclic impact loadings and effect of static loads on damage evolution[J]. Chinese Journal of Rock Mechanics and Engineering, 2014,33(8):1162-1171.
[9] Wang Lili. Foundation of stress waves(second edition)[M].Beijing: National Defence Industry Press,2005.(in Chinese)
杂志排行
Journal of Beijing Institute of Technology的其它文章
- Combustion Properties of Metal Particles as Components of Modified Double-Base Propellants
- Optimization of Crosswalk Width Based on Bi-Directional Pedestrian Crossing Time at Signalized Intersections
- Efficient Activation Method of Hardware Trojan Based on Greedy Algorithm
- Estimation of Thermal Imaging System Operating Range Based on Background Radiation
- Network Sorting Algorithm of Multi-Frequency Signal with Adaptive SNR
- Log Likelihood Ratio-Based Relaying for Distributed Turbo Codes
