潜在因子构造与货币政策溢出效应:基于中美两国的实证比较
2018-06-15位雪丽刘程程
位雪丽,刘程程
(1.河南财经政法大学 经济学院,郑州 450000;2.中央财经大学 统计与数学学院,北京 100081)
0 引言
随着国家之间的联系日益紧密,一个国家的货币政策不仅在国内发挥作用,而且会通过各种渠道传导至其他国家,从而造成本国货币政策在国内的实际效果与预期效果产生偏离。同时,伴随经济周期发生的资产价格的国际联动现象使得识别并评估货币政策溢出效应更为困难,因此,关于货币政策在国家之间的传导渠道与溢出效应程度的讨论至今没有定论。对货币政策国际溢出效应的深入研究有助于货币政策制定及实施之前的效果预判,提高货币政策有效性,也有助于国家之间的货币政策协调。
现有研究更加关注美国货币政策对其他国家经济变量的溢出影响[1-5],并且大多使用固定系数VAR模型研究货币政策的溢出影响,而国家之间的关系以及国家内部各经济变量之间的关系均随时间而变,具有时变系数的模型更合适。另外,大量非常规货币政策的使用导致常规货币政策变量对货币政策效果的刻画程度逐步减弱,需要选择更具代表性的货币政策变量。因此,本文结合具有时变特征的FAVAR模型来构造两国的经济活动因子和价格水平因子。创造性地选取中美两国股市指数作为货币政策变量,同时采用中国的广义货币供应量M2和美国的联邦基金利率等常规性货币政策变量进行稳健性研究。并采用TVP-SVAR模型来研究中美两国的货币政策溢出效应,综合考察各经济变量间的动态关系。
1 因子构造
为客观反映样本期内中美两国的经济活动情况及价格走势,本文以中美两国为研究对象,分别选取两国的基础经济活动指标和价格水平指标。在TVP-FAVAR模型基础上分别构造中美两国的经济活动因子和价格水平因子,对其货币政策溢出效应进行研究。
1.1 因子构造框架——TVP-FAVAR模型
若用xt(t=1'…'T)表示n×1维的用于提取因子的经济变量,则P阶滞后的TVP-FAVAR模型描述如下:
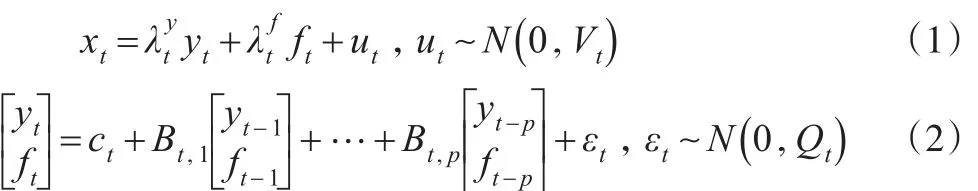
其中,yt是控制变量;是用于反映yt对xt影响程度的回归系数;ft是包含公共信息的潜在因子,代表xt的整体走势;是表示 ft对xt影响程度的因子载荷;(Bt'1'…'Bt'p)是VAR模型的系数向量,用于反映yt和 ft之间的动态关系;ct是截距项;ut和εt均是0均值的高斯扰动项,相应的方差Vt和Qt均具有时变性,为保证扰动项ut中包含的是异质冲击,特假定Vt为对角阵。基于TVP-FAVAR模型构造的两国的潜在因子均具有时变性,既能反映经济变量的整体变化趋势,又能避免模型的过度参数化问题。
公式(1)用于从xt中提取经济活动和价格水平两类潜在因子。首先,在预测因子组合变量时使用包含潜在因子的多变量模型,可以将控制变量、潜在因子与因子组合变量之间的依赖关系刻画得更加准确;其次,通过在模型中加入控制变量可以消除其对潜在因子的影响,使得 ft仅反映与xt相关的信息。
公式(2)表示 ft与 yt的动态交互作用,λt=((λyt)′'()′)′是代表控制变量和潜在因子影响程度的载荷向量,是模型的系数向量,刻画了控制变量和潜在因子之间的动态关系,基于时变性而假定两类参数均为多维随机游走过程。
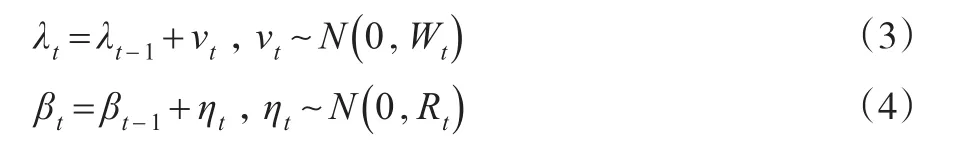
假定上述四个公式中的随机扰动项之间相互独立,均不存在自相关性,模型方差的异质性体现在Vt和Qt上,参数λt和βt的时变性体现在Wt和Rt上,由此便是TVPFAVAR模型的完整表达。
1.2 变量选取及数据处理
在价格稳定和最大就业的双重目标下,泰勒规则描述了央行在价格和就业分别偏离其目标值时的政策利率调整路径。鉴于经济产出和通货膨胀在制定货币政策中的重要性以及数据可得性,本文从CEIC数据库中分别摘取了反映中美两国经济整体变动情况和人民币购买力变化趋势的月度数据,样本期为2000年1月至2016年6月,分别构造中美两国的经济活动因子和价格水平因子。其中,中国经济活动因子用到的数据包括工业总产值、固定资产投资等28个变量;中国价格水平因子用到的数据包括消费者价格指数、消费者核心价格指数等4类变量;美国经济活动因子用到的数据包括工业生产指数、消费者信心指数等9个变量;美国价格水平因子用到的数据包括城市消费者价格指数、能源部门消费者价格指数等4类变量。
参照Fernald等(2014)[6]的数据处理方法,同时考虑到中国与美国的国情差异,根据两国的实际情况对原数据进行处理。对于中国数据,首先,考虑到中国新年数据的突变特点,本文假定各变量每年12月份至2月份之间的增长率相同来调整数据,以消除各变量在此期间的不合理变动;其次,使用X-12季节调整法消去季节影响;最后,通过对数差分变换得到各变量平稳的增长率序列。美国数据相对来说较为完整,只需先进行X-12季节调整,再通过对数差分变换得到变量稳定的增长率序列即可。

图1 中国经济活动因子与中国工业总产值
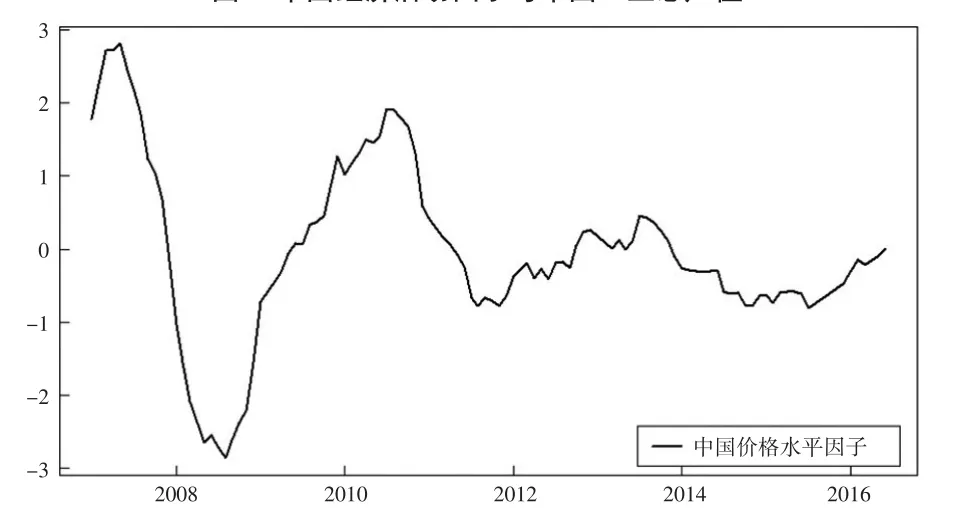
图2 中国价格水平因子
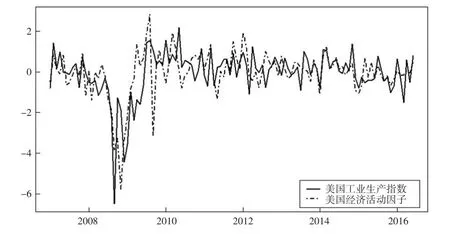
图3 美国经济活动因子及美国工业生产指数
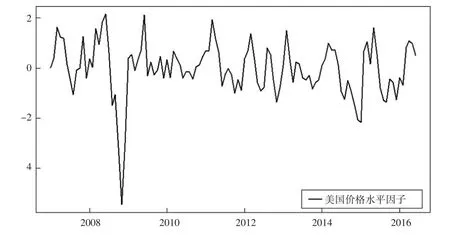
图4 美国价格水平因子
1.3 因子构造及拟合效果评价
由于多变量的联合后验分布形式复杂,从中抽样时需使用马尔科夫链方法,使得应用贝叶斯法估计TVP-FAVAR模型参数时成本较高,因而本文借鉴Doz等(2011)[7]的两步估计法构造潜在因子。首先,使用主成分分析法从因子变量集合中提取主成分,以反映大量经济变量的整体走势,并使用最小二乘法估计模型以得到参数和潜在因子的初始值;其次,基于卡尔曼平滑法来重新估计模型以得到新的估计值,来代替参数和潜在因子的初始值。根据中美两国的经济变量和滞后阶数判断准则,确定TVP-FAVAR模型的滞后阶数为4,在此基础上分别得到中美两国的经济活动因子和价格水平因子,见图1至图4①本文使用2000年1月至2016年6月的数据构造因子,整体拟合程度大致相同,出于可视化考虑,仅画出金融危机以来的因子及相关变量走势。。
图1是中国经济活动因子及中国工业总产值的趋势拟合图,图2是中国价格水平因子的趋势拟合图。对比两张图的走势发现,两因子均有效地刻画了金融危机期间经济活动和价格水平先大幅下降之后又大幅上升的趋势。由于TVP-FAVAR模型允许参数和方差时变,因而构造的潜在因子可以更有效地捕捉不同时期起主导作用的因素波动,准确刻画样本期间经济活动和价格水平的走势。与此同时,本文将中国工业总产值与中国经济活动因子作比较,从图1可以看出用潜在因子具有很好的代表性。由于中国经济活动因子在构造时考虑了更多的经济信息,因此,在金融危机期间,其下降程度要大于工业总产值,说明金融危机对经济的总体影响程度要大于其对工业总产值这一单一经济指标的影响程度。
图3反映了美国的经济活动变化趋势,图4是美国价格水平的趋势拟合图。从两因子的大致走势可以看出,二者均可有效捕捉2008年全球金融危机对美国经济活动和价格水平的冲击。图3中美国经济活动因子与美国工业生产指数的走势大致吻合,说明构造的经济活动因子对美国经济具有较好的代表性,二者之间的差异可由因子构造时使用变量的多样性及丰富性来解释。总体上看,构造的美国经济活动因子和美国价格水平因子能很好地刻画美国的经济状况和价格趋势。
对比中国和美国的经济活动因子及价格水平因子可以发现,两国的经济和价格波动具有不同的波动特征:首先,相对于美国,中国的经济和价格波动频率较低;其次,中国的经济和价格走势具有明显的周期性,而美国没有。结合两个国家的四个潜在因子来研究货币政策溢出效应,重在关注金融危机以来中美两国货币政策溢出效应的变化趋势,以准确反映中美两国货币政策溢出效应的传导渠道及影响程度,为制定合理的货币政策提供参考依据。
2 变量选取及数据处理
本文借鉴Giovanni等(2016)[8]的做法,将常规货币政策变量(中国的M2和美国的联邦基金利率)和非常规货币政策变量(股市指数)共同纳入模型来研究非常时期的货币政策的溢出效应。中美两国的货币政策变量走势对比如图5和图6所示。

图5 中国货币政策变量
图5是将中国的不同货币政策变量(M2、上海证券交易所综合指数、深圳证券交易所综合指数)进行趋势对比所得结果。整体上看,样本区间内中国的广义货币供应量M2的变动趋势与两个股市指数的变动趋势大致相同。自2013年以来,为更好地管理中短期流动性,中国央行综合使用多种非常规货币政策工具,导致M2与两个股市指数的变动趋势存在一定程度的偏离。综合来看,将股市综合指数作为货币政策变量具有合理性。同时,由于两个指数走势基本相同,且均能很好地反映我国货币政策实施以后的市场流动性情况,因此,下文研究货币政策溢出效应时仅选择上海证券交易所综合指数作为货币政策变量。
图6是将多个美国货币政策变量(联邦基金利率、纽约股票交易所综合指数)进行趋势对比所得结果。从中可以看出,美国的联邦基金利率与其股市指数的变化趋势具有一致性,并且在捕捉政策变动方面股市指数更具优势:美联储在金融危机期间进行过10次降息操作,导致联邦基金利率降至0%~0.25%,零利率限制了联邦基金利率作为货币政策变量的有效性,并且之后美联储进行的量化宽松及前瞻性指引操作所引起的经济变化均不能反映在联邦基金利率的变化上。而纽约股票交易所综合指数则能很好地反映这种情况,这也说明将纽约股票交易所综合指数作为美国货币政策变量具有说服力。
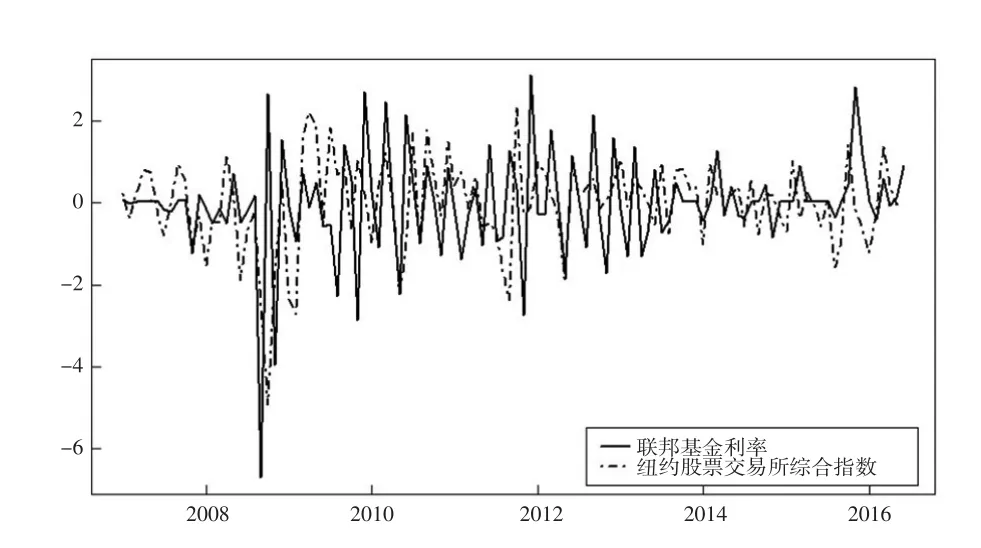
图6 美国货币政策变量
3 实证分析框架——TVP-SVAR模型
TVP-SVAR 模型首先由 Primiceri(2005)[9]提出,被广泛用于研究货币政策冲击。本文基于中美两国经济活动因子、价格水平因子和两国货币政策变量构造具有时变特征的TVP-SVAR(p)模型,通过分析中国和美国的货币政策对两国经济变量和政策变量的脉冲响应图来研究货币政策溢出效应。为实现估计过程,首先将TVP-SVAR(p)模型转变为TVP-VAR(p)模型并估计参数,再进行参数还原得到TVP-SVAR(p)模型的估计值。TVP-SVAR(p)模型形式如下:

模型转化之后得到如下形式的TVP-VAR(p)模型:
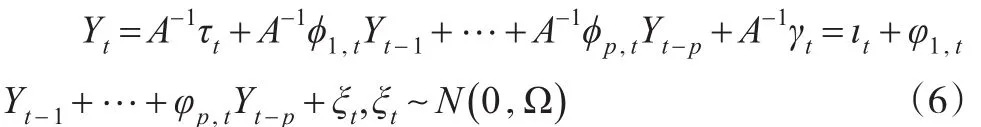
在具体估计过程中,需要将其转变为状态空间的表示形式:

其中,Yt是由中美两国的经济活动因子、价格水平因子和货币政策变量组成的可观测向量;Φt是由多个随时间而变的参数组成的不可观测状态向量,用于反映TVP-VAR(p)模型的时变性;H是连接可观测向量与不可观测状态向量的系数矩阵;ξt是观测方程的随机扰动向量,ζt是状态转移方程的随机扰动向量,ξt与ζt不相关且均为白噪声过程。本文需要估计的内容包括TVP-VAR(p)模型中状态转移方程的参数κ、状态变量Φt、状态转移矩阵F及方差协方差矩阵Σ、观测方程的方差协方差矩阵Ω,用到的方法包括Gibbs抽样法[10]和贝叶斯统计方法中的 Carter-Kohn(1994)算法[11]。
在估计TVP-VAR(p)模型之后,选择符号约束法[12]来实现TVP-SVAR(p)模型的参数识别过程。用符号约束法进行TVP-SVAR(p)模型识别过程中能有效避免较为严格的等式约束[13],解决短期约束的约束性过紧问题。符号约束法的核心思想是依据经济理论直接限定货币政策冲击对相关经济变量的影响方向,以帮助识别模型参数识别,同时也填补了TVP-VAR(p)模型不具备理论基础的空白。值得一提的是,对于冲击方向不确定或者研究者较为感兴趣的“新息”,可以不对相关经济变量的反应方向做出限定,而是让其依据样本数据所包含的信息来主动显示变动方向,降低先验信息不准确对模型估计带来的偏误问题。本文在模型识别过程中,针对一国货币政策冲击,仅对本国经济活动和价格水平的反应方向做出限定,而其他国家的经济活动、价格水平和货币政策等变量则根据样本数据信息主动选择反应方向,据此考察货币政策的溢出效应。结合滞后阶数判断准则及中美两国经济活动因子和价格水平因子的数据长度,将模型的滞后阶数设为2,合理设定迭代次数以确保结果收敛,并尽量降低先验设定对估计结果的影响,最后在Gibbs抽样算法和贝叶斯推断方法下完成对TVP-SVAR(2)模型的估计。
4 货币政策溢出效应的实证
4.1 中国货币政策的溢出效应
为保证实证结果的稳健性,本文分别选择了不同的货币政策变量,并同时将中国的货币政策变量、两国的经济活动因子和两国的价格水平因子同时放入TVP-SVAR(2)模型进行脉冲响应分析。样本区间内不同时期的脉冲响应走势不同,可以直观反映出不同时间上相同货币政策冲击的对国内外经济变量的影响程度,这得益于模型系数的时变性。在使用符号约束识别TVP-SVAR(2)模型时,仅限定中国货币政策变量对中国经济活动和价格水平的影响方向,并不限定对美国相应因子的影响方向,在缺乏相关研究的情况下做出如此设定极为必要。在1个单位标准差(序列在样本区间内随机波动的均值)的货币政策冲击规模下,得到三维脉冲响应图,如图7和图8所示。
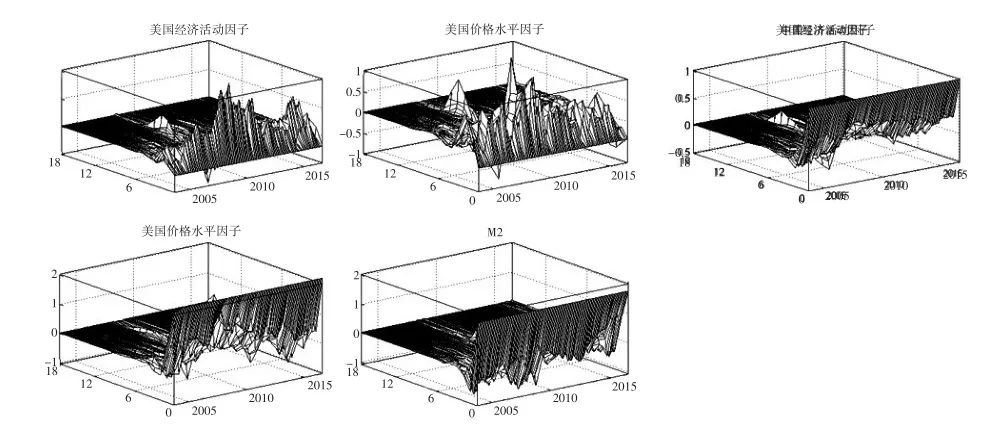
图7 中国货币供应量冲击的脉冲响应图
图7和图8反映了中国货币政策对中美两个国家的经济活动因子和价格水平因子的脉冲响应情况。分析发现,无论是M2还是上海证券交易所综合指数,1单位正向冲击对中美两国的经济活动及价格水平均有影响,且影响具有时变性,尤其在金融危机期间,冲击影响呈现出波幅增大持续期延长的特征。对比分析发现,图7中M2冲击对美国经济活动和价格水平的影响相对较小,且各期变化方向基本一致,只是程度有所不同,其中金融危机期间影响较大。图8中上海证券交易所综合指数冲击对美国的影响则呈现金融危机前期由正震荡至零,金融危机后期由负逐渐震荡降为零的特征。两种情况下,正常年份中的影响
持续期为6个月左右,但在2010年前后,其影响期明显延长,在18期(一年半)结束时影响依然明显。在虚实背离的特殊情况下,货币刺激使得虚拟经济快速膨胀,股市流动性激增,导致货币政策与股市指数的变化逐步趋同。同时M2对市场流动性的刻画程度逐步降低,因此相对于M2,上海证券交易所综合指数更能代表中国货币政策的宽松程度,其对美国的冲击影响更能代表美国的真实反映。
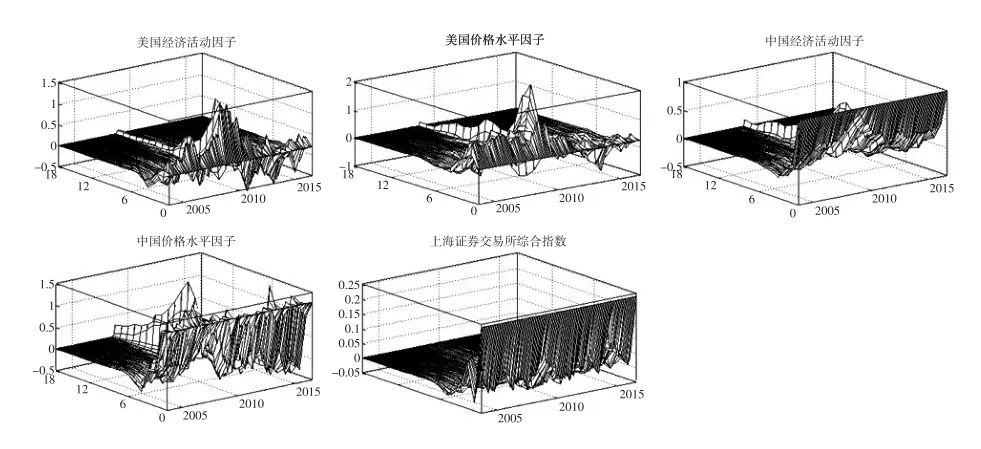
图8 中国股市指数冲击的脉冲响应图
4.2 美国货币政策的溢出效应
图9和图10为美国货币政策变量对中美两个国家经济活动因子和价格水平因子的脉冲响应图。分析发现,无论是联邦基金利率还是纽约证券交易所综合指数,美国的货币政策冲击均对中国的相关因子存在明显冲击,且初始影响为正,并逐渐震荡减弱。相比两种情况,从对中国经济活动因子的影响来看,图10中美国货币政策冲击的影响呈现从高位逐步震荡下降至零的现象,而图9中则表现出大幅度的上升和下降。从对中国价格水平因子的影响来看,图10中的震荡幅度明显降低,且呈现双向波动趋势,而图9中则呈现出大幅度的正向影响,且能持续一段时间。

图9 美国联邦基金利率冲击的脉冲响应图
基于图7至图10的实证分析发现:第一,中国货币政策对美国经济活动和价格水平具有明显影响,同时美国货币政策也明显影响中国的经济活动和价格水平。并且两种影响在金融危机期间呈现出波幅增大持续期延长的特征,表明中美两国的货币政策均存在明显的溢出效应;第二,从脉冲响应图的时间维度看,金融危机后中国货币政策对美国相关变量的影响幅度有下降趋势。同时,美国货币政策对中国相关变量的影响变化主要体现在价格水平上,也存在明显减小现象。说明中美两国受他国货币政策溢出效应影响的程度均在减弱,一定程度上证实了两国的货币政策独立性均在日益增强。
图10 美国股市指数冲击的脉冲响应图
5 结束语
本文使用TVP-FAVAR(4)模型构造经济活动因子及价格水平因子,并在不同货币政策变量下分别使用TVP-SVAR(2)模型进行实证研究,认为中美两国货币政策间存在明显的溢出效应,且这种溢出影响具有时变性。货币政策溢出效应不仅会降低该政策在国内的有效性,同时也会对其他国家的经济变量造成影响。因此,随着经济演变过程的不断发展,需要基于不同货币政策工具的特点,适时调整货币政策策略,加强正向溢出,避免负向溢出,提高货币政策的整体实施效果。本文的主要贡献在于:第一,在单个指标对经济走势的代表性不断降低的情况下,使用TVP-FAVAR(4)模型构造潜在因子,便于整体观察货币政策对大量指标的综合影响,提高实证结果的合理性;第二,使用股市指数作为货币政策变量,扩展了传统货币政策变量的使用范围;第三,使用TVP-SVAR(2)模型研究货币政策溢出效应,便于观察溢出影响随时间的变化趋势及不同时期的货币政策有效性。
[1]吴宏,刘威.美国货币政策的国际传导效应及其影响的实证研究[J].数量经济技术经济研究,2009,(9).
[2]Hausman J,Wongswan J.Global Asset Prices and FOMC Announcements[J].Journal of International Money and Finance,2011,30(3).
[3]胡援成,张朝洋.美元贬值对中国通货膨胀的影响:传导途径及其效应[J].经济研究,2012,(4).
[4]张晶.美国持续低利率政策对中国货币政策的影响分析[J].财贸经济,2013,(4).
[5]何国华,彭意.美、日货币政策对中国产出的溢出效应研究[J].国际金融研究,2014,(2).
[6]Fernald J G,Spiegel M M,Swanson E T.Monetary Policy Effectiveness in China:Evidence From a FAVAR model[J].Journal of International Money and Finance,2014,(43).
[7]Doz C,Giannone D,Reichlin L,et al.A Two-Step Estimator for Large Approximate Dynamic Factor Models Based on Kalman Filtering[J].Journal of Econometrics,2011,164(1).
[8]Giovanni G,Nour T.Spillovers From Japan’s Unconventional Monetary Policy to Emerging Asia:A Global VAR approach[R].IMF Working Paper,WP/2016/99.
[9]Primiceri G E.Time Varying Structural Vector Autoregressions and Monetary Policy[J].The Review of Economic Studies,2005,72(3).
[10]Canova F.Methods for Applied Macroeconomic Research[M].Princeton:Princeton University Press,2007.
[11]Carter C,Kohn R.On Gibbs Sampling for State Space Models[J].Biometrika,1994,81(3).
[12]Uhlig H.What Are the Effects of Monetary Policy on Output?Results From an Agnostic Ldentification Procedure[J].Journal of Monetary Economics,2005,52(2).
[13]Granville B,Mallick S.Monetary Policy in Russia:Identifying Exchange Rate Shocks[J].Economic Modelling,2010,27(1).
