油气水多相管流预测方法研究
2018-06-15王修武廖锐全陈元虎
王修武,罗 威,刘 捷,廖锐全,陈元虎
(1.长江大学,湖北 武汉 430100;2.中国石油气举试验基地多相管流实验室,湖北 武汉 430100;3.中国石化江苏油田分公司,江苏 扬州 225000)
0 引 言
多相管流的研究已经有30多年的历史,研究得到的多相管流预测方法有二十几种,被广泛应用的多相流计算方法接近10种。多相管流预测方法按导出原理可分为半经验、经验模型[1-5]和机理模型[6-7]。尽管如此,多相管流还存在很多不完善和亟待解决的实际问题。早前,由于实验条件有限(介质、流量范围、测量仪器精度[8]等),能在油、气、水三相流基础上得到的多相流计算方法较少。近年来,中国著名科研院所开始侧重于稠油多相流动方面的研究[9],直接忽略了对常规黏度原油与气、水三相流动的系统性研究。利用国外流行工程计算软件PIPSIM、中国编制多相流计算软件对中小产量、较高气油比油井进行多相流预测,与实测数据对比表明,目前已有多相流计算模型预测压力结果普遍偏高;而对中高产量、较高气油比油井进行多相流预测,与油田实测数据对比表明,目前已有多相流计算模型预测压力结果普遍偏低[10]。针对以上问题,目前缺少常规黏度原油、气、水三相流动的系统性研究[11-12]。鉴于此,开展了常规黏度油、气、水三相流动的系统性实验研究,并在此基础上开展了多相管流涉及到的流型、持液率、压降3个方面的预测模型研究。
1 流型预测模型验证及优选
在多相管流流型图研究方面,目前比较认可和备受关注的多相管流流型预测方法有Zhang Hongquan[6]、L.E.Gomez[13]、Kaya[14]、J.J.Xiao[15]、Beggs-Brill[5]、Barnea[16]、Mukherjee-Brill[8]。其中,Zhang Hongquan和Kaya属于流型预测机理模型,L.E.Gomez和J.J.Xiao对流型的研究较少,Beggs-Brill、Barnea、Mukherjee-Brill属于流型预测,非机理模型。鉴于此,开展了油、气、水三相流研究,实验模拟参数如表1所示。将通过实验绘制流型图版(高速摄像机拍摄和肉眼观察相结合)与现有模型绘制流型图版进行对比,如图1所示。Zhang Hongquan模型和Beggs-Brill模型的实验条件均为51 mm管径,空气或水为介质,倾角为20 °。
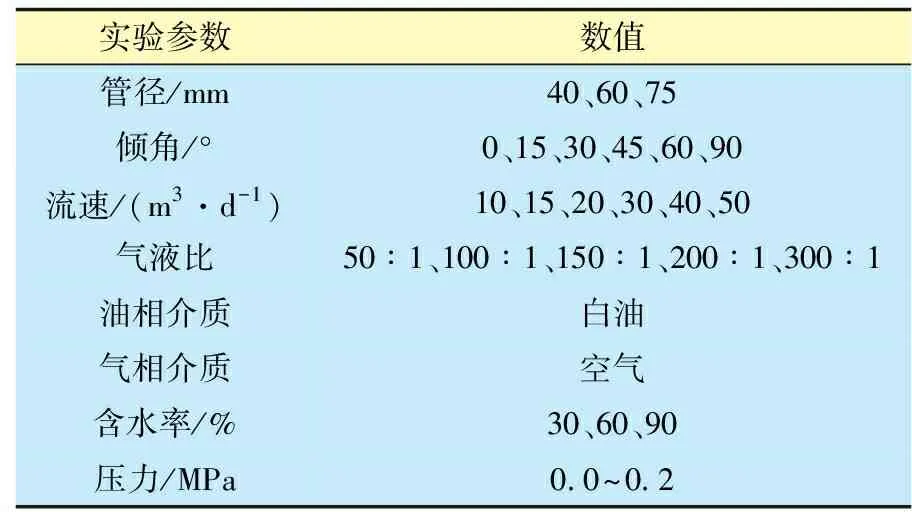
表1 实验模拟参数选择
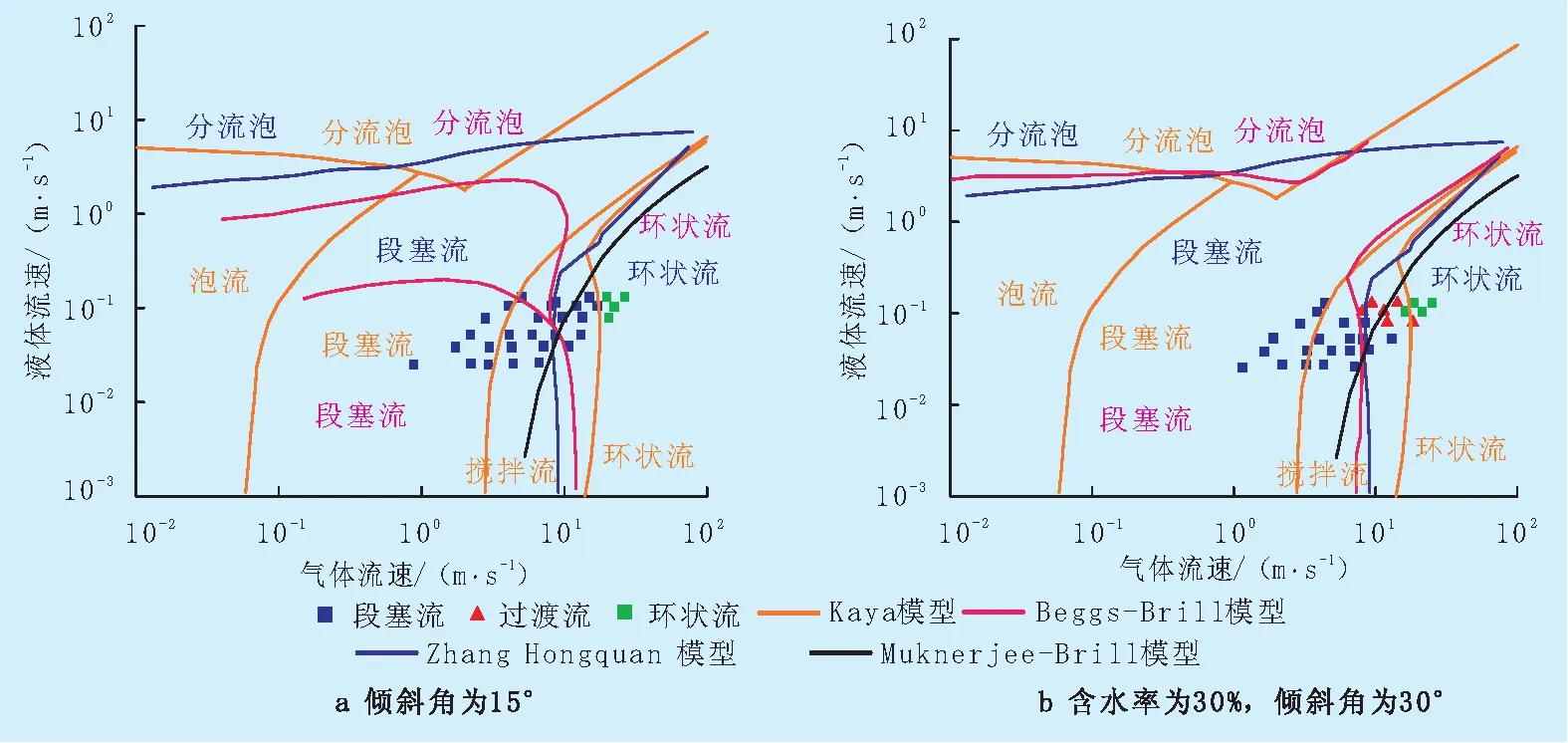
图1 不同含水及倾角多相流实验绘制流型图与现有流型图对比
由图1可知,流型预测方法存在不准确的地方。从总体上看,Mukherjee-Brill模型预测流型效果最好,Zhang Hongquan模型在倾斜角为60~90 °时流型预测效果较好,Barnea模型水平流型预测较好。因此,优选Mukherjee-Brill流型预测模型作为研究预测流型。
2 持液率和压降预测模型验证及拟合
2.1 持液率和压降预测模型准确性验证
在多相管流持液率和压降预测方面,首先采用实验数据对常用的6种多相流计算方法进行压降预测验证(表2),并对其中2种具有持液率计算能力的方法(Beggs-Brill、Mukherjee-Brill)进行持液率预测验证(表3)。
2.2 不同组合条件下持液率计算误差分析
对上述2种具有持液率计算能力的多相流方法分别进行4种不同组合条件下的压降预测对比(表4、5)。其中,4种不同组合条件为:A为持液率、流型和压降均预测,B为持液率给出、流型和压降均预测,C为流型给出、持液率和压降预测,D为流型和持液率给出、压降预测。
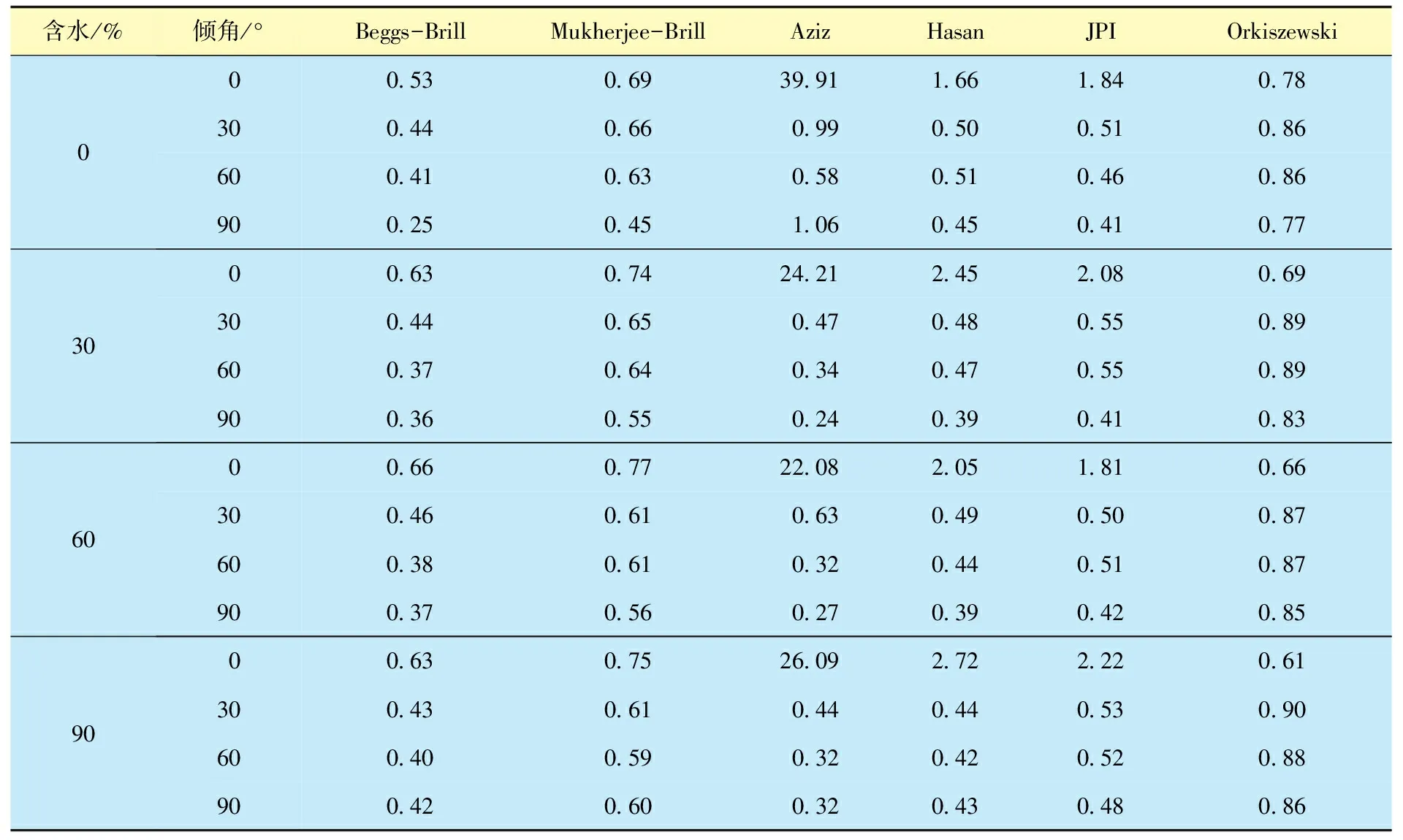
表2 6种方法压降预测平均误差统计
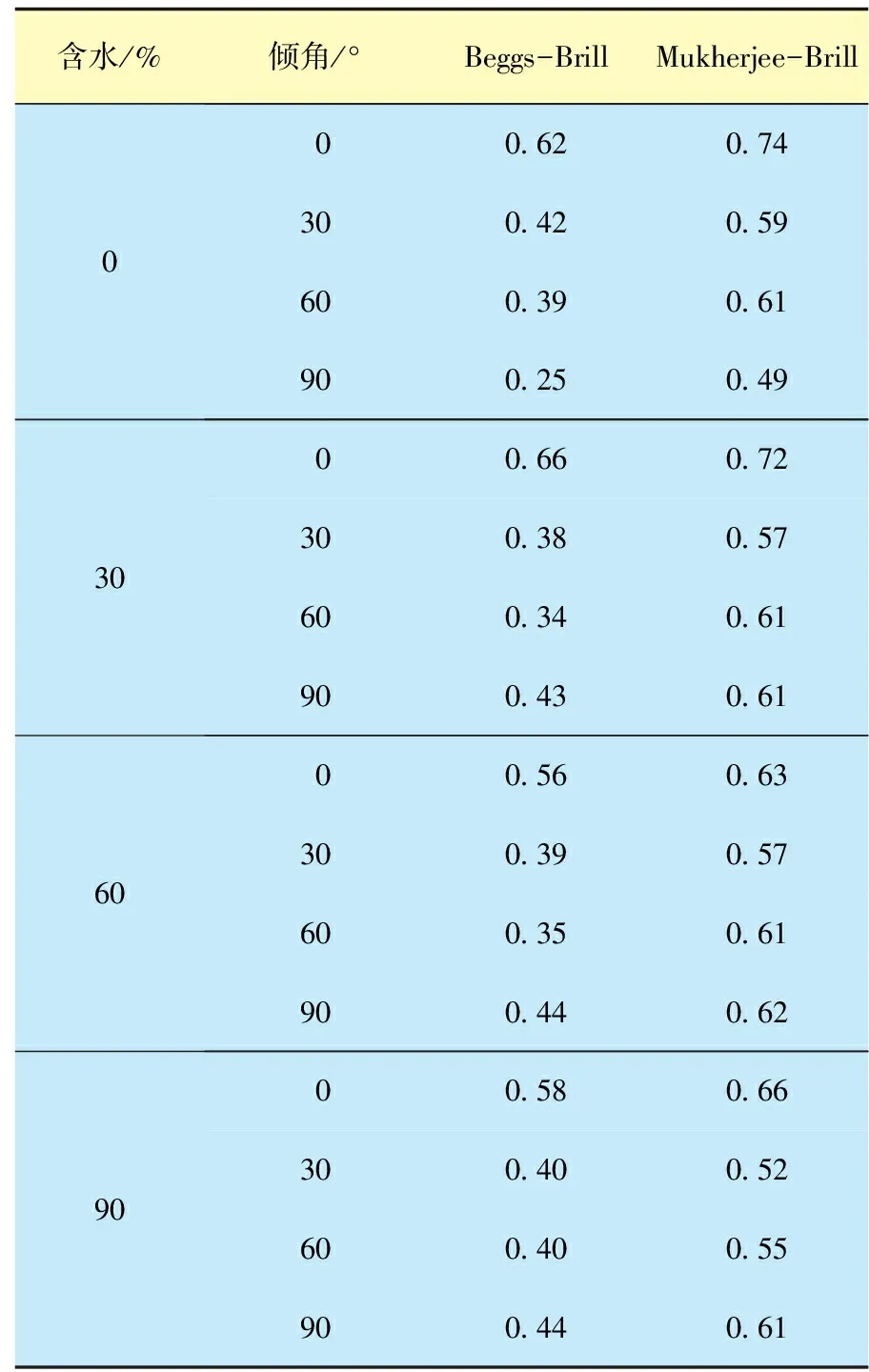
表3 2种方法持液率预测平均误差统计
由表4、5可知,不同组合方法下,当给出持液率时,与其他组合条件下相比,压降预测准确率大大提高。这也说明,准确预测持液率能大大提高倾斜管流压降预测的精度。
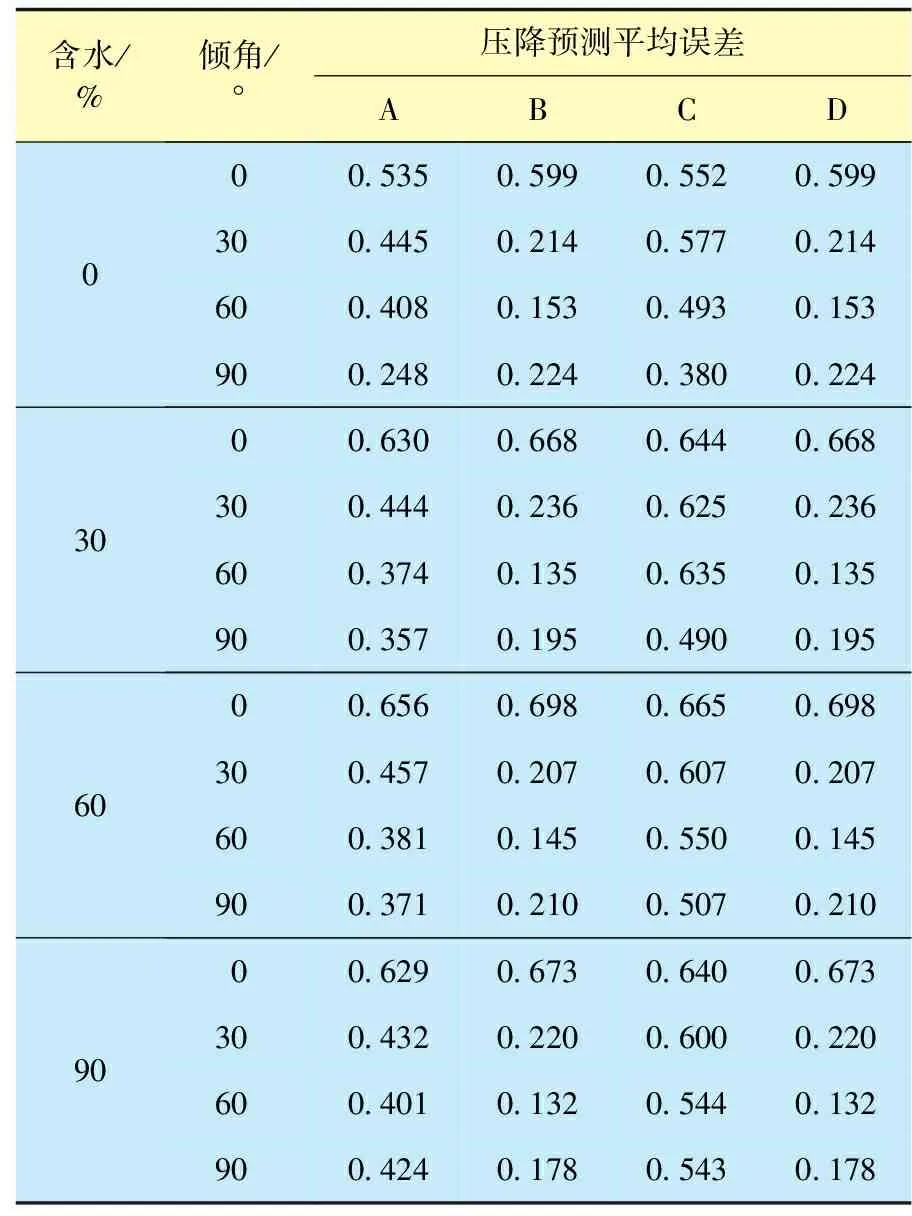
表4 Beggs-Brill方法不同组合条件压降预测平均误差统计
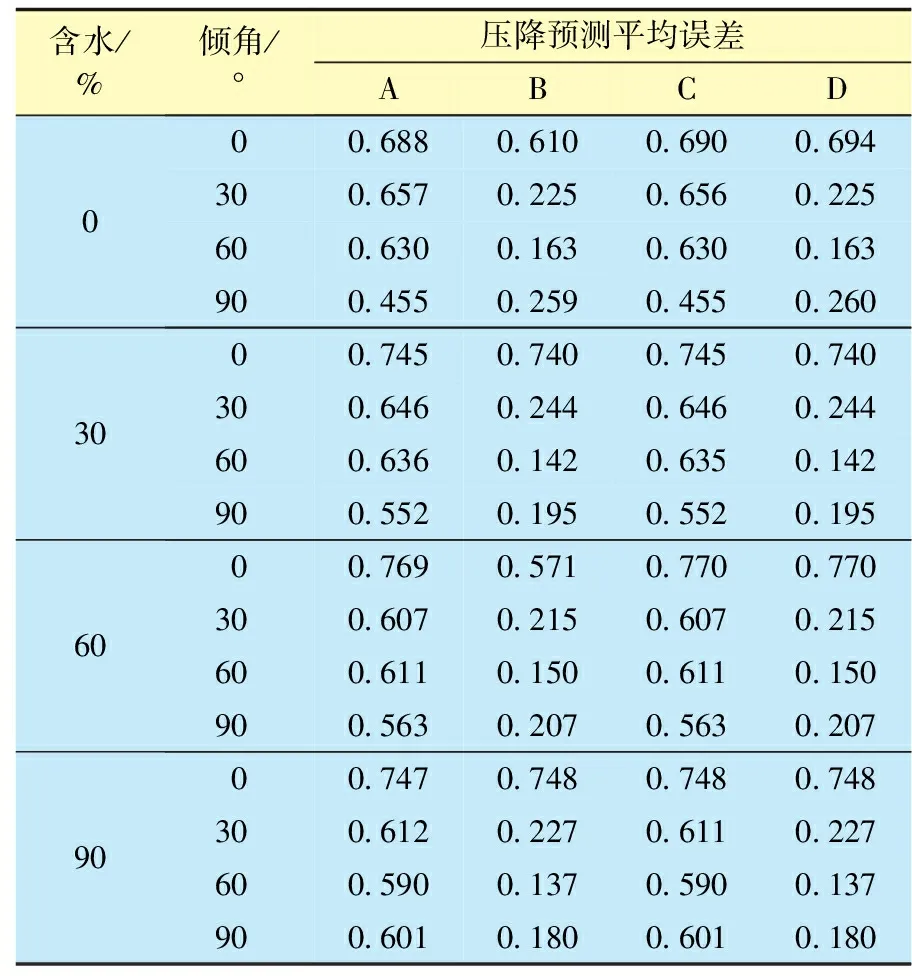
表5 Mukherjee-Brill方法不同组合条件压降预测平均误差统计
同时,对Beggs-Brill方法和Mukherjee-Brill方法进行不同组合条件下持液率预测检验,结果如表6、7所示。
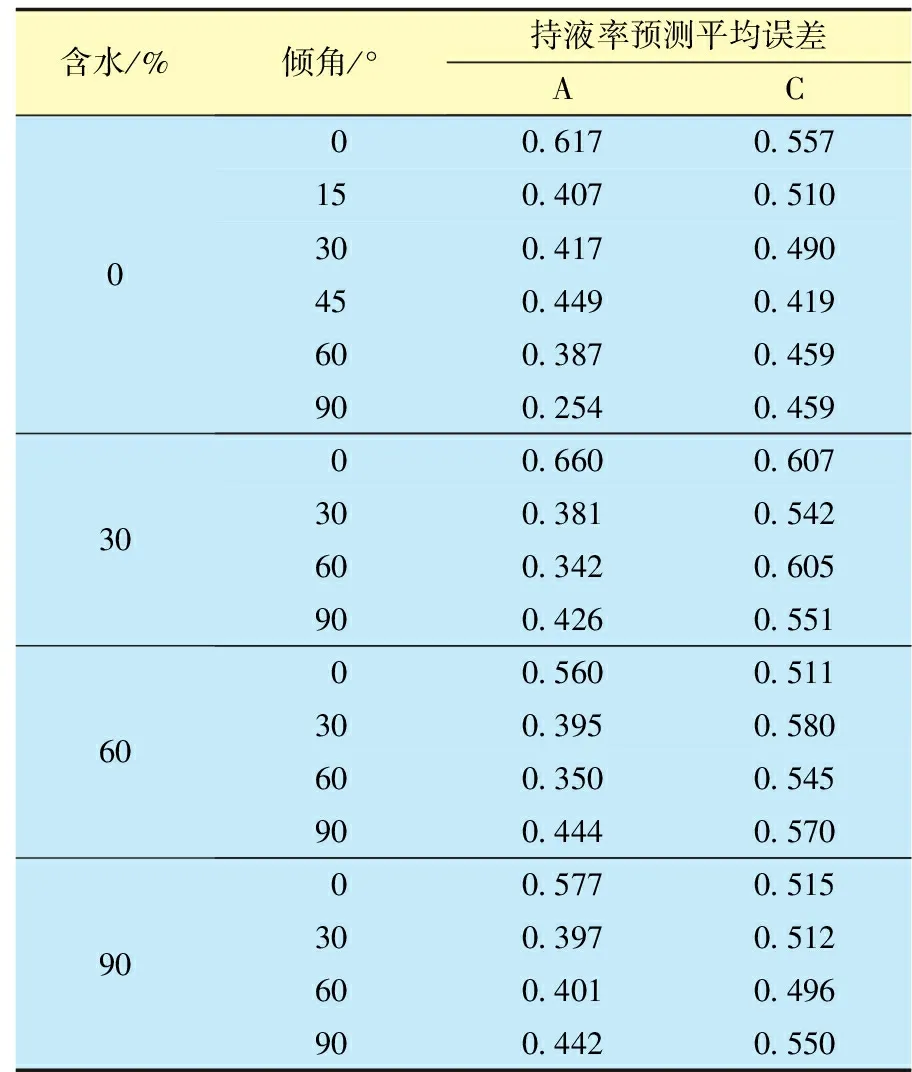
表6 Beggs-Brill方法不同组合条件持液率预测平均误差统计
由表6、7可知,Beggs-Brill方法流型预测与实际有较大差别,倾斜段预测存在较大偏差,因此,给出流型时,持液率计算误差差别较大,而Mukherjee-Brill则基本相同,进一步验证该模型流型图判断的准确性。
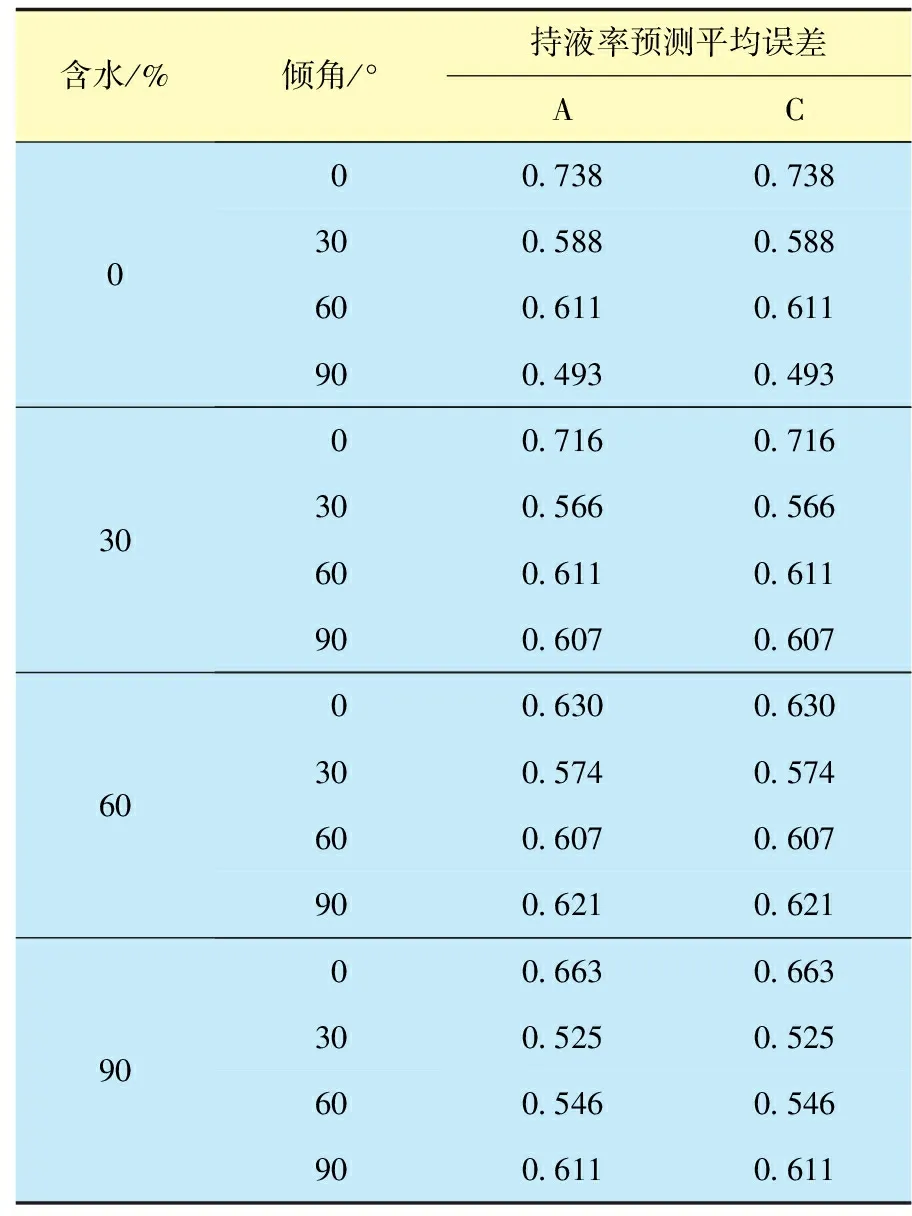
表7 Mukherjee-Brill方法不同组合条件持液率预测平均误差统计
2.3 持液率预测模型拟合
鉴于持液率的预测准确性对压降预测影响较大,准确预测持液率能够大幅度提高压降预测准确性。基于常规黏度油气水三相多相管流系统性实验数据(40、60、75 mm 3种管径、不同倾角、不同含水率条件)对Mukherjee-Brill[14]的持液率计算结果进行了重新拟合。由表7可知,水平状态和倾斜状态计算误差差别较大,因此,对水平和倾斜2种条件分别进行了拟合(表8)。
3 新预测模型验证和误差分析
分别从实验数据、现场实测数据对新预测模型进行验证。由于新模型是在系统性实验数据基础上拟合得到,因此,首先需要通过实验数据对新模型进行检验,验证其与实验数据的符合情况,即验证拟合过程的正确性,再通过现场实测数据对新预测模型进行检验。
3.1 实验数据对新模型的检验
持液率和压降预测结果与实验数据之间平均误差如表9所示。
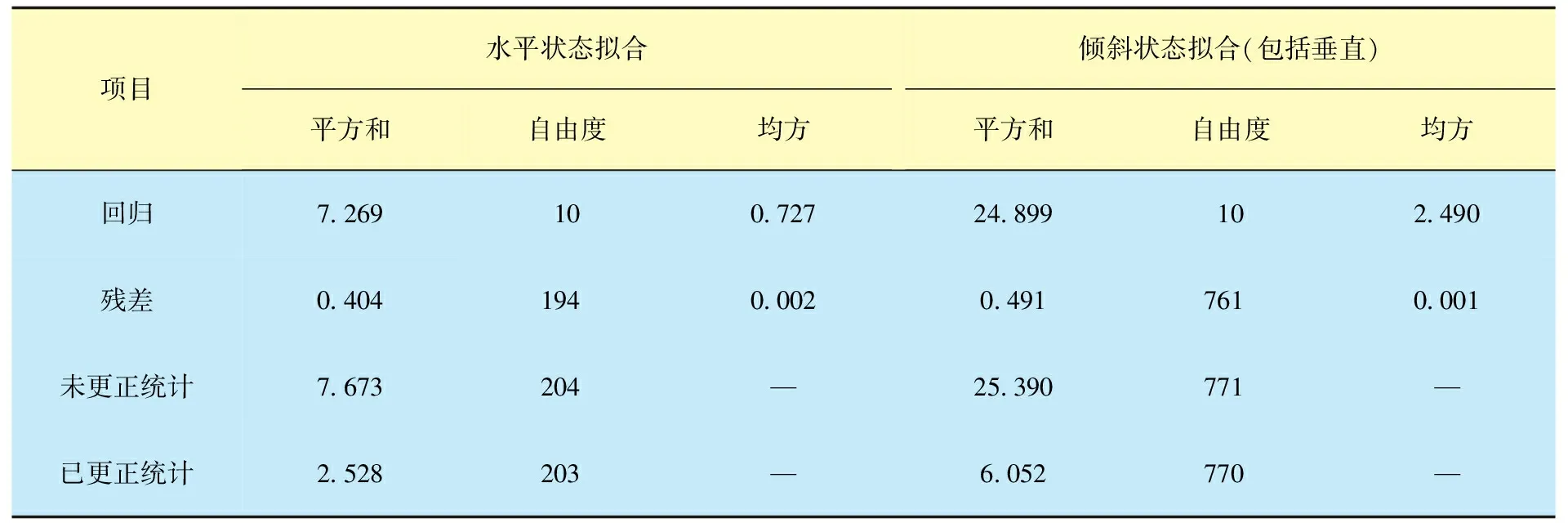
表8 水平状态、斜井状态持液率拟合结果

表9 新模型预测结果与实验数据平均误差统计
将表9与表2、3、5、7对比可知,持液率预测和压降预测精度均有较大提升,在倾斜状态(包括垂直状态)可以满足工程计算预测需要,证明拟合方法过程可行;由于水平管流压降中摩阻项占主导,持液率重新拟合后压降预测精度提升较小,而倾斜管流压降中重力项占主导,持液率预测准确后该项预测精度提升幅度较大。
3.2 现场实测数据对新模型检验
以新疆玛湖油田多口生产井的实测流压数据为例,对现有常用的6种井筒多相管流计算方法和新模型进行压力预测验证。
3.2.1 实测数据
统计玛湖地区7井次(5口井,测试井套管管径为139.7 mm,油管平均倾斜角为0 °)的测试数据(表10)。
3.2.2 预测结果误差分析
通过实测数据对7种多相管流压力预测方法(包含新模型)进行检验,计算结果平均误差统计如表11所示。
由表11可知,新预测模型平均相对误差最小,为5.08%,其次为Mukherjee-Brill[14]方法,为8.53%。现场实测数据验证表明,以实验数据为基础建立的多相管流预测模型可降低多相管流压降预测误差,新预测模型可用于现场多相管流压力分布预测。
4 结 论
(1) 在多相管流流型划分方面,结合实验对流型图版对比发现,最适合的流型判断方法为Mukherjee-Brill方法。
(2) 实验数据检验表明,现有6种多相流压降预测方法误差均较大,准确预测持液率能极大提高倾斜管流压降预测的准确性,进一步说明Mukherjee-Brill方法流型预测的准确性。
(3) 对Mukherjee-Brill持液率方法进行了重新拟合,检验表明,新模型拟合效果较好,且其倾斜管流压降预测误差明显降低。现场实测数据验证表明,新预测模型较其他模型预测精度至少提高3个百分点,预测更加可靠。
(4) 研究表明,倾斜管流压降中重力项占主导,持液率预测准确后,压降预测精度提升幅度较大,而由于水平管流压降中摩阻项占主导,持液率重新拟合后压降预测精度提升较小。
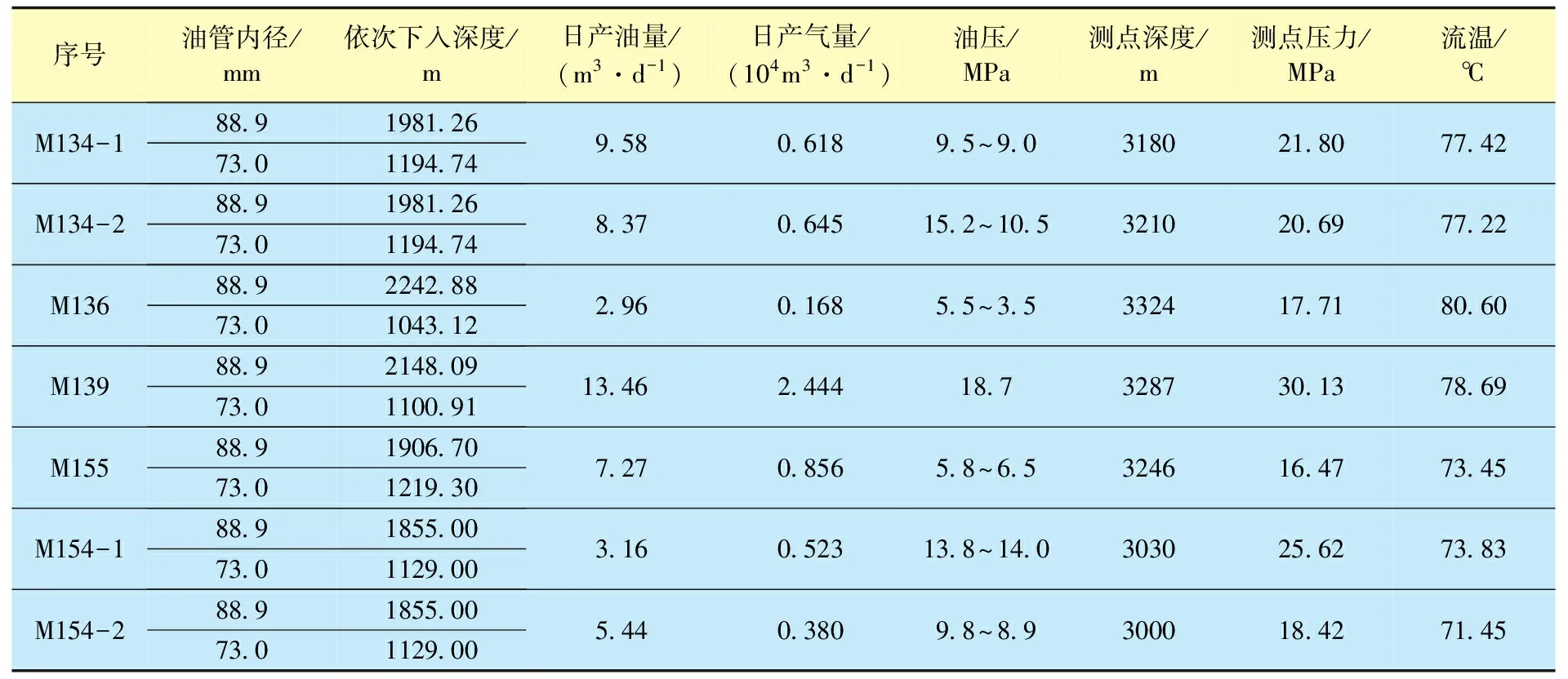
表10 7井次(5口井)测试数据统计

表11 压力计算平均相对误差统计(平均7井次)
[1] DUNS H J,ROS N C J.Vertical flow of gas and liquid mixtures in wells[C].WPC10132,1963:451-466.
[2] HAGEDORN A R,BROWN K E.Experimental study of pressure gradients occurring during continuous two-phase flow in small-diameter vertical conduits[J].Journal of Petroleum Technology,1965,17(4):475-484.
[3] ORKISZEWSKI J.Predicting two-phase pressure drops in vertical pipe[J].Journal of Petroleum Technology,1967,19(6):829-838.
[4] AZIZ K,GOVIER G W.Pressure drop in wells producing oil and gas[J].Journal of Canadian Petroleum Technology,1972,11(3):38-48.
[5] BEGGS D H,BRILL J P.An experimental study of two-phase flow in inclined pipes[J].Journal of Petroleum Technology,1973,25(5):607-617.
[6] WANG S,PEREYRA E,SARICA C,et al.A mechanistic slug liquid holdup model for wide ranges of liquid viscosity and pipe inclination angle[C].OTC-24046,2014:329-336.
[7] WANG S,ZHANG H Q,SARICA C,et al.A mechanistic slug-liquid-holdup model for different oil viscosities and pipe-inclination angles[J].SPE Production & Operations,2014,29(4):329-336.
[8] 李颖川.采油工程[M].北京:石油工业出版社,2002:41-43.
[9] NOSSEN J,LAWRENCE C J.Pressure drop in laminar slug flow with heavy oil[C].BHR-A006,2012:91-104.
[10] WANG S.Experiments and model development for high-viscosity oil/water/gas horizontal and upward vertical pipe flows[D].Oklahoma:University of Tulsa,2012.
[11] 张荣军,陈军斌,任月玲,等.水平井筒中流型识别的数学方法[J].特种油气藏,2009,16(2):67-69.
[12] 丁景辰.致密气藏同步回转增压排水采气工艺[J].特种油气藏,2017,24(3):145-149.
[13] GOMEZ L,SHOHAM O,SCHMIDT Z,et al.A unified mechanistic model for steady-state two-phase flow in wellbores and pipelines[C].SPE56520,1999:1-14.
[14] KAYA A S,SARICA C,BRILL J P.Mechanistic modeling of two-phase flow in deviated wells[J].SPE Production & Facilities,1999,16(3):156-165.
[15] XIAO J J,SHOHAM O,BRILL J P.A comprehensive mechanistic model for two-phase flow in pipelines[C].SPE20631,1990:167-180.
[16] BARNEA D.A unified model for predicting flow-pattern transitions for the whole range of pipe inclinations[J].International Journal of Multiphase Flow,1987,13(1):1-12.
