有取向颗粒的布朗运动模拟研究

邹全胜

1 概述

众所周知，布朗运动是小颗粒在分子的无规则热运动下受到来自各个方向的撞击而引发的无规则动力学运动，是分子动理论的著名证据之一。分子在永不停息的、无规则的热运动中不断撞击宏观物体的表面，给予其表面上的随机分布力。对于一般的宏观物体，由于其表面积和质量都较大，故在每一时间段内受到大量分子的撞击，且一定大小冲量所引起的速度改变更小，由于统计理论中随机变量所具有的抵偿性，故随机合力的增长幂次较之宏观物体的质量的增长幂次小，很难在宏观上观察到其无规则运动。但对于小到介观尺度的颗粒，例如，其尺度小到微米甚至纳米级别，则统计涨落的重要性开始显现，在每一时刻，随机分布力都无法充分抵偿而形成某一随机方向的合力，这就是布朗运动的成因。[1]

随着显微技术的发展，人类对微小对象的认知越来越直观和精细。1827年英国植物学家R.布朗通过用显微镜观察水溶液中的花粉颗粒，布朗运动由此被人们所熟知。充分体现了生产力和技术的发展对科学进步的推动作用。在今天，电子计算机的广泛使用使得计算和模拟成为研究物理问题的强大而高效的手段。[1]布朗运动可以抽象为数学中的随机行走模型，用计算机来模拟颗粒的布朗运动，可以非常方便地研究诸如布朗运动的位移期望与时间的关系等诸多问题。这一类工作已经有很多文献介绍过。[2-3]但是，如果进行布朗运动的小颗粒不再视为各向同性的球体，例如，纳米棒材料，那么会得出什么新的结论？

纳米棒材料，例如金纳米棒，具有丰富的物理化学性质，近年来在材料科学中得到了越来越广泛的关注。在生物医学、催化化学、传感器和光学器件方面都有重要应用[4]。是否能够找到一种基本的、模拟其运动规律的计算方法？这是用计算机模拟来代替实验操作而进行纳米棒各种应用的探索的基础性工作之一。

纳米棒具有取向性，其布朗运动的自由度更高，角量自由度在布朗运动中会如何变化？由角量自由度描述的旋转是否与平动存在耦合？本文考虑在流体介质中纳米棒的二维布朗运动，以动力学方程为依据建立可在计算机上运行的随机行走模型，将模拟结果绘制成图，并得出反映有取向颗粒布朗运动的关键性质的若干重要结论。

2 动力学模型

2.1 朗之万方程

描述各向同性颗粒(如小球)的布朗运动的动力学方程为郎之万方程[5]：

其中，F代表随机出现的布朗力。用随机行走模拟此布朗运动时，普遍采用的算法是设定一个步长，每一步都以等概率向任何一个方向迈出此步长[2-3]。

对于纳米棒，一方面它的随机行走并不能轻易断言为各个方向等概率等距离的——垂直与取向和沿着取向的情况，从直观上看并不会一样。另一方面，在随机行走的过程中，所需要关注的并不仅限于质心的坐标，还有取向的坐标，或者说取向与坐标轴的夹角——也就是纳米棒的自转。

2.2 随机力的简化模型

接下来将建立模拟二维平面上纳米棒的布朗运动的模型，简明起见，纳米棒简化为长a宽b的矩形。

对于被大量分子包围的矩形，其边界上每一处都会承受大量分子的撞击而有垂直于边界的压强。因此矩形边界上每一点都受到一个法向随机力，这些随机力可以理解为成对出现的：矩形上每一点所受到的随机力都对应于对边上同一点所受到的分布一致、反向、共线的随机力。这一对力的合力的期望为零，呈正态分布，分别在长方体的两条轴线上铺开。

各向同性颗粒的随机行走模拟中，每一帧何方向迈出一步，可以理解为每一帧随机受到某一点的一个力，与此类似，对随机力作以下设定：在每一帧，矩形上的某一点受到单个的力，为了更加简化，可以直接设定每次力的大小都一样，由此代替呈正态分布的随机力，这在统计意义上并不会引起差异。

2.3 平均力的简化模型

除了涨落引起的随机力外，流体的阻力等平均力是不可忽略的。对流场中物体受力的计算是一个十分复杂的问题，流体力学中的基本方程是纳维-斯托克斯方程：

▽p+pF+μΔv

要用此方程来解析求解平面平行运动的矩形所受的阻力和阻力矩，将会十分困难。目前主要的计算方法除了直接数值求解动力学方程外还有格子玻尔兹曼方法等[6]。本文采用一种易于计算的简单假设，来考虑流体对纳米棒的整体作用：当固体边界各处存在一定法向速度分布时，统计上看前进方向前端的边界将会受到更多流体分子的碰撞。假设流体分子的速度分布服从气体的麦克斯韦分布律，与边界法向发生一维弹性碰撞而改变动量，只需考虑这一方向上速度的分布律：

f(v)=Ae-λv2

在单位时间Δt内，对长ΔL的一小段固体壁，如果以向内的法向速度u前进，则对于法向速度为v的粒子群，只有面积为ΔS=ΔL(v-u)Δt的流体分子会与其发生弹性碰撞，由于流体分子质量远小于纳米棒，故单个分子的动量改变为Δp=2m(v-u)。如果流体分子的面密度为σ(在二维情况下)，则速度分布在v附近dv区间的粒子所造成的总的动量改变dΔp=2σΔS(v-u)f(v)dv。

将不同速度对应的面积代入，则所有速度大于u的分子的总动量变化为：

这个积分本质上是不完全伽马函数，但是由于布朗运动的速度在数量级上远远小于分子热运动速度，故可以用泰勒展开进行近似：

其中，第一项是边界静止时的平均压强，它显然是一个定值。对任意简单闭曲线，它本身和它的一次矩的积分都为0，这意味着它不提供合力和合力矩。第二项则是边界有法向速度时对压强的线性影响，运动方向前端的边界所受压强更大，后端的边界所受压强更小，呈现阻力的特征，这与预期相符。为了便于计算，本文中忽略切向的粘滞力，假定流体对颗粒的整体阻力为正比于边界法向速度的压强。

3 步长的设置

3.1 平动步长

可见，对于不同尺寸的纳米棒，步长也是不同的。可以考虑以1*1的纳米棒(正方形纳米颗粒)为基准，设定一个步长S。在程序中我们设定S=0.05。

通过计算机程序，可以实现在矩形的两条轴线上以等概率随机取点。

3.2 转动步长

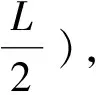
平动在之前已经论述过，有

F=f=Lαv

即平动步长的平方和边长成反比，S在程序中设定为0.05。例如，对于16*5的纳米棒，如果力作用在长边上，则此帧的移动距离为0.0125。

现在计算转动角速度为w时粘滞阻力所产生的力矩。

当纳米棒绕中心转动时，边界承担阻力，对于其中一条承担阻力的边界：

v(x)=ωx

df=αv(x)dx=αωxdx

dM=xdf=αωx2dx

则四条变边界段所受合力矩：

为了达到力矩平衡，有

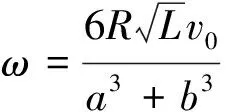
以上分别导出了对于任何给定的随机力，这一阵帧行走时应走的步长和角度。至此，用逐帧随机行走模拟纳米棒的随机行走的算法已经完成。

4 模拟结果

在计算机上编写相应程序，就可以用蒙特卡洛方法模拟上述的过程。以下展示一些典型的模拟结果。

4.1 纳米方块( 1*1)的一次随机行走

这是正方形的纳米棒，并且作为校对步长的基准。以下是2万步质心坐标路径图和角度变化趋势(图1，图2)。

图1

图2

由于步长设置得很短，因此2万步并没有走太远，覆盖面积和1*1的纳米方块尺寸比起来只有大约几十倍。角度的变化范围大约在2-3个圆周内。

将取向作为z轴，画三维图(图3)。

图3

4.2 小纳米棒(4*1)的一次随机行走

作出4*1小纳米棒质心坐标路径(图4)，角度变化趋势(图5)及三维图(图6)，可以看出同样是两万步的结果，因为尺寸变大，所以角度的变化比1*1纳米方块缓和。

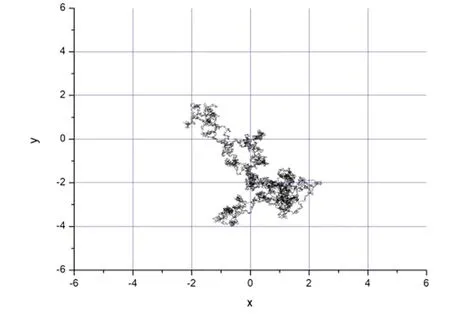
图4

图5

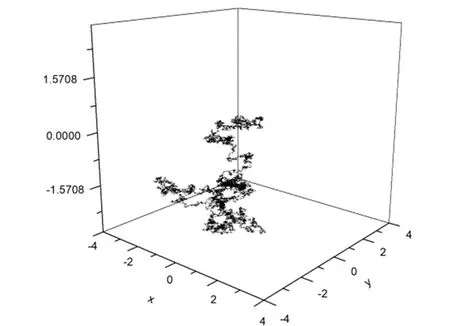
图6

4.3 大纳米棒(40*10)的一次随机行走

将4*1纳米棒换为形状相同、100倍大的，观察随机行走，作出相应模拟图(图7，8，9)。

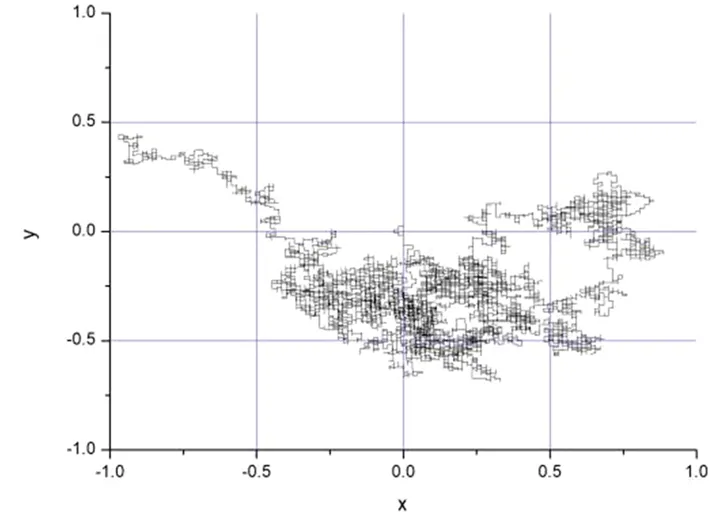
图7

图8

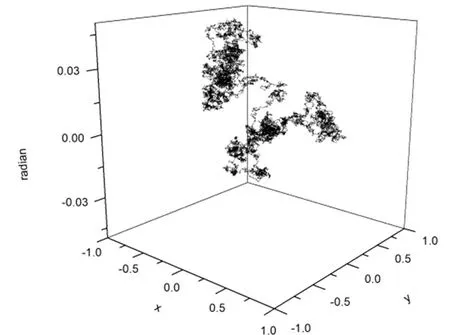
图9

可以明显看到移动范围小得多，最远距离原点不到1。角度变化和之前相比也非常小，2万步最大转动不到十分之一弧度。

4.4 随机行走与颗粒尺寸的关系

对比4*1纳米棒和40*10纳米棒，可以很明显地看到：同样长宽比的纳米棒，当尺度变大时，布朗运动会变得缓和。这很容易理解，因为在前文的分析中已经指出步长的平方与边长成反比。从物理角度上说，考虑到随机事件的抵偿性，当研究对象的尺寸变大时，分子撞击的统计涨落将会越来越大的样本容量所覆盖。很显然，我们只能在花粉等小颗粒上观察到明显的布朗运动，而较大的物体则几乎体现不出布朗运动。

5 重要性质

在绘制了纳米棒布朗运动的图像后，进一步对数据进行定量分析，可以得出一些重要结论。

5.1 平均行走距离

验证平均行走距离随时间的演化。选取不同尺寸的纳米棒分别进行1000次8万步的模拟，并分别对这1000次中每一帧的质心到原点距离的平方。

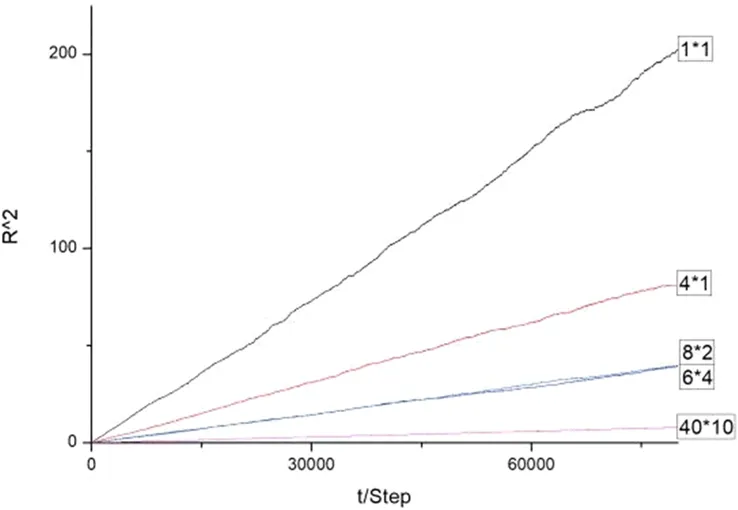
图10

如图所示，R2的期望与t大体上成正比。这正是数学中随机行走理论的一个重要结论。[7]与匀速运动中R与t的正比关系不同，随机行走的移动效率将越来越低。在有取向的颗粒的布朗运动中，平方正比的关系并没有被破坏，说明转动并不影响平动的整体效应。

另一方面，对比4*1、8*2、40*10三个纳米棒的斜率满足10:5:1的关系，而且8*2和6*4几乎重合，说明在本文所使用的模型中，R2的期望与纳米棒的周长成反比，与形状无关。

5.2 取向的自关联系数

某一时刻的自关联系数定义为此时取向方向单位向量与初始取向方向单位向量的内积，表征对初始取向的“记忆”随时间的衰减。由于初始条件都设为纳米棒的取向指向x轴正方向，故计算自关联系数即是计算取向的余弦的平均值。

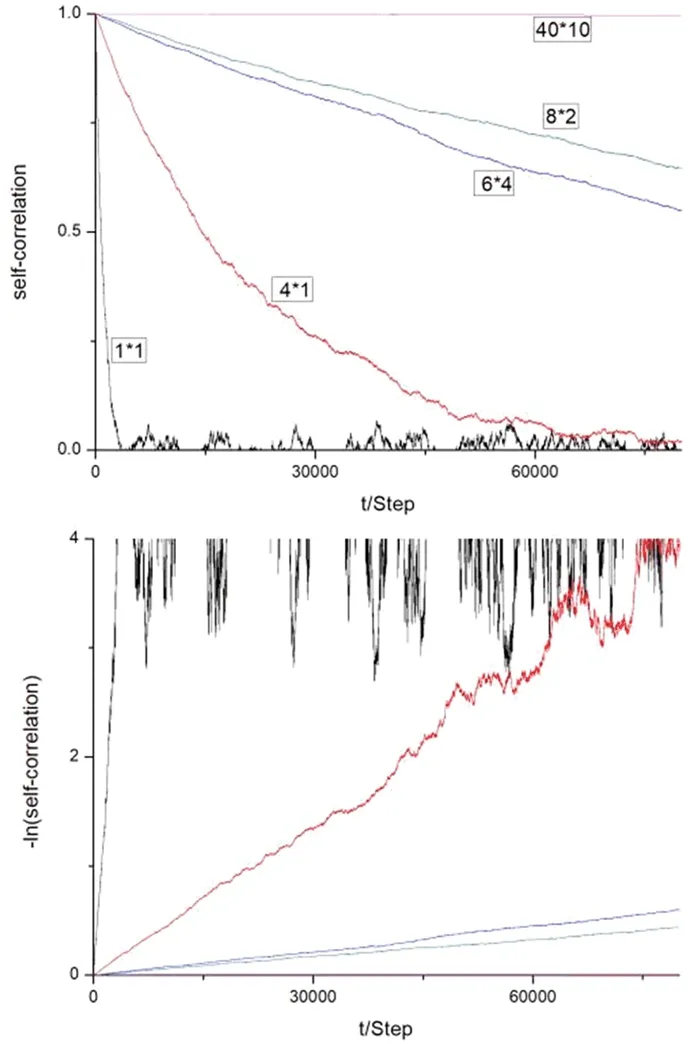
图11

左图分别画出了不同尺寸的纳米棒在随机行走中取向的自关联系数的变化规律。定性来说，前半段是上凹函数，从1衰减到0附近，之后开始震荡。尺寸越小的纳米棒，衰减的速度越快，衰减完毕后震荡得越剧烈。例如1*1纳米方块在几千步长之内迅速衰减到0，而8*2/6*4纳米棒则一直到走完8万步都只是衰减到0.6-0.7左右，40*10在8万步之内几乎没有衰减。

用半对数坐标重绘左图。取纵坐标为自关联系数的负对数，得到右图。可以看出，在开始震荡之前，自关联系数的负对数与t大体呈线性的线性关系。这表明在本文的模型中，自关联函数随时间呈指数衰减。

[r(0)·r(t)]=exp(-kt)

k是比例系数。

衰减到0附近后，开始无规则震荡。

容易理解，越小的纳米棒，则衰减得越快，k越大。正如前文所述，越小的纳米棒布朗运动越剧烈，则原来的取向在布朗运动中会快速丢失。而大的纳米棒，例如本实验中40*10纳米棒，布朗运动很小，取向的随机改变也很慢，能够保存很长时间。至于宏观尺度上的物体，布朗运动不可能导致其取向改变。

在原先取向的“记忆”衰减殆尽后，纳米棒的取向就与原始取向不再有关联性。不过自相关函数之后的噪声又提出了一个新的问题，这可能是计算机性能有限、样本容量不够大所致的统计涨落，不应存在于解析结果中。

[参 考 文 献]

[1] 郝柏林.布朗运动理论一百年[J].物理,2011,40(1):1-7.

[2] 谢征微,李玲.布朗运动的计算机模拟[J].四川师范大学学报(自然科学版),1997(1):97-100.

[3] 王莱.布朗运动和随机行走的计算机仿真[J].工科物理,1998(6):47-49.

[4] 杨玉东,刘公召,徐菁华,杨林梅,李冬至.金纳米棒:合成、修饰、自组装、SERS及生物医学应用[J].中国科学:化学,2015,45(6):581-596.

[5] 王竹溪.统计物理学导论[M].北京：高等教育出版社,1965.

[6] 聂德明,林建忠.模拟颗粒布朗运动的格子Boltzmann模型[J].浙江大学学报(工学版),2009,43(8):1438-1442.

[7] 张波,张景肖.应用随机过程[M].北京：清华大学出版社,2004.