改进SVM算法在引水明渠纵向离散系数优化中分析

董天奥

(辽宁省江河流域管理局，辽宁 沈阳 110003)

河流纵向离散系数是分析污染物物迁移变化特征的重要参数，对于河流污染保护规划十分重要。当前，对于河流纵向离散评估的主要手段还是采用数值优化求解的方式进行评估求解[1- 5]，进行数值优化求解就要涉及采用什么样的优化方法进行求解，才能保证其优化求解的精度。近些年来，具有较强搜索优化能力的SVM方法在数值优化求解计算中应用较为成熟[6- 9]，但是近期有学者发现传统SVM方法在泛化求解精度上有所局限，并针对此类问题进行了改进。为此文章结合改进的SVM方法对某引水明渠的纵向离散系数进行优化求解，研究目的在于分析该优化算法在引水明渠的纵向离散系数优化求解的适用性。

1 改进SVM算法原理

SVM算法主要基于混沌算法进行数值优化求解，优化方程为：

xn+1=uxn(1-xn)

(1)

在方程(1)中表示算法的控制变量，当u=4时，构成连续的混沌系列x0，x1，…，xn。在构建完成混沌样本序列后，计算目标函数的适宜度，计算方程为：

(2)

式中，y′—试验测定的纵向离散系数；yi—目标函数值。改进的SVM方程采用两类空间函数对模型样本序列进行优化表征，空间优化函数为：

f(x)=w·φ(x)+b

(3)

式中，x—空间混沌变量；w—双向变量权重；b—混沌样本系列最小值。在确定优化空间函数后，需要进行决策变量的计算，计算方程为：

f(x)=w·φ(x)+b=0

(4)

则方程转换为：

(5)

在进行决策变量计算时，需要满足变量间隔最小的计算条件：

yi(WTxi+b)-1≥0

(6)

改进的SVM算法约束条件设定为：

(7)

改进算法结合拉格朗日方程进行最优点的数值求解，加强方程的泛化能力：

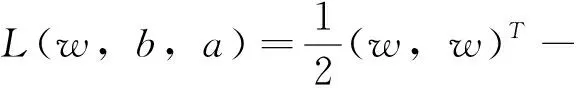
(8)

式中，ai—拉格朗日因子，方程可以进行偶数变化：

(9)

基于算法的约束条件，可以对混沌系列的进行不同类别的优化计算，方程为：

(10)

在经过决策变量分析后，得到最终的优化目标求解函数：

a*-(a1*,a2*,…,al*)

(11)

方程(10)中k为改进SVM算法的核心函数。文章采用高斯函数来进行核心函数的计算求解：

(12)

在确定核心函数基础上，可以确定改进SVM算法的最终方程：

(13)

从方程中可以看出σ和C为方程的两个优化敏感函数；C为算法的结构误差因子。

2 水槽物理模型试验概况

本次模型试验在辽宁省水工程试验研究中心的多功能试验厅内完成，现场如图1所示。厅内设有各种水泵、高位水箱和容积为1000m3、300m3的地下水库各1座，最大循环供水量1000L/s。配套设施有Micro ADV声学多普勒流速仪一套，URI-Ⅲ型河床模型地形测量系统一套，活动控制室1间，以及多种测量、测试设备。流量由槽首的矩形堰量测，矩形堰宽1.0m，高0.6m，堰板采用厚度为1cm的有机玻璃制成。水位采用水位测针量测。

图1 水槽试验现场图

3 试验结果

3.1 模型试验样本分析

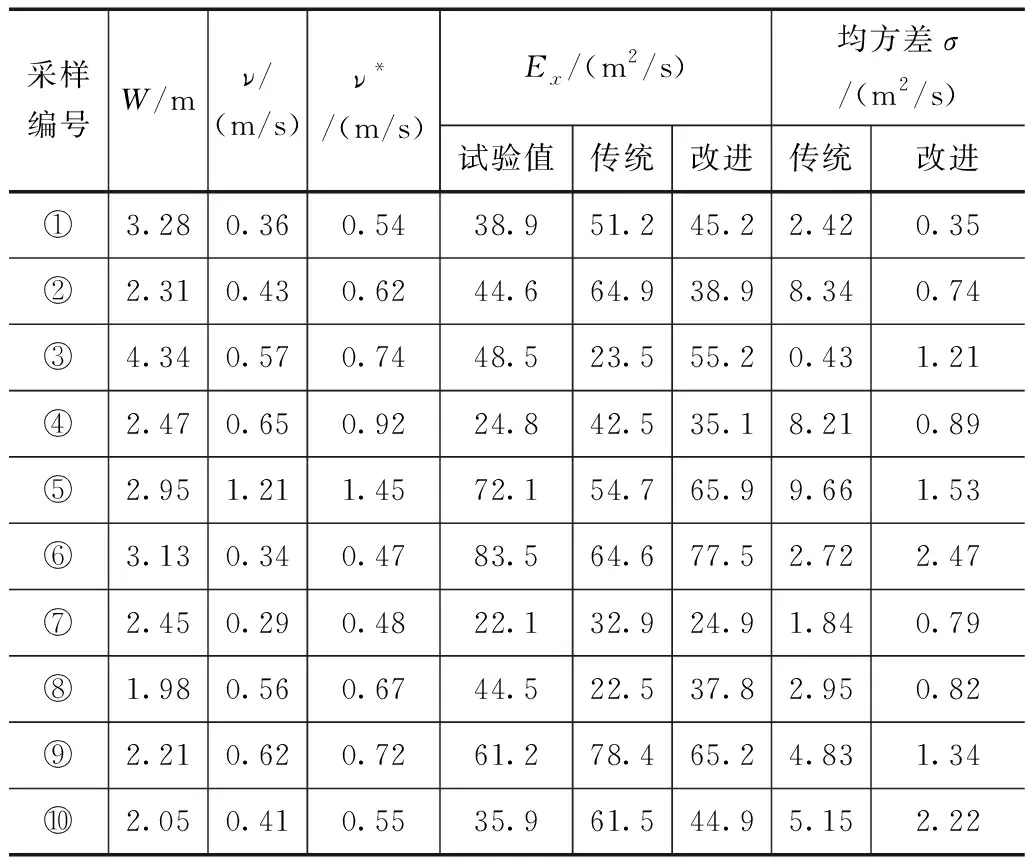
进行了10个断面的水槽试验测定，对各水槽的水深H、宽度W，及纵向流速ν和剪切流速ν*进行了测定，输出变量为采样水槽试验进行示踪法测定的纵向离散系数Ex，试验样本分析结果见表1，并在试验结果的基础上，分析了不同变量与纵向离散系数Ex相关敏感度，结果如图2所示。

表1 水槽试验测定结果

由表1和图2可以看出，水槽示踪试验测定的各样本纵向离散系数和水面宽度的相关敏感度最高，其次是纵向流速，纵向流速的大小直接决定纵向离散系数的大小，剪切流速以及水深对纵向离散系数影响相对较小。

3.2 模型试验结果对比

为对比分析改进前后的SVM算法对引水明渠纵向离散系数的影响，结合试验测定的纵向离散系数以及断面形态特征变量，对比分析改进前后算法的纵向离散系数优化精度，分析结果见表2，如图3所示。

从表2可以看出，相对于改进前的SVM优化算法，改进后的SVM算法在引水明渠纵向扩散系数的优化精度上得到一定程度的提高。这主要是因为改进后的SVM优化算法增强了模型优化求解的泛化能力，使得模型优化求解速率增强，提高了纵向扩散系数求解收敛度。从图3可看出，误差分布较为平均，改进算法下的相关集中度更为聚集。

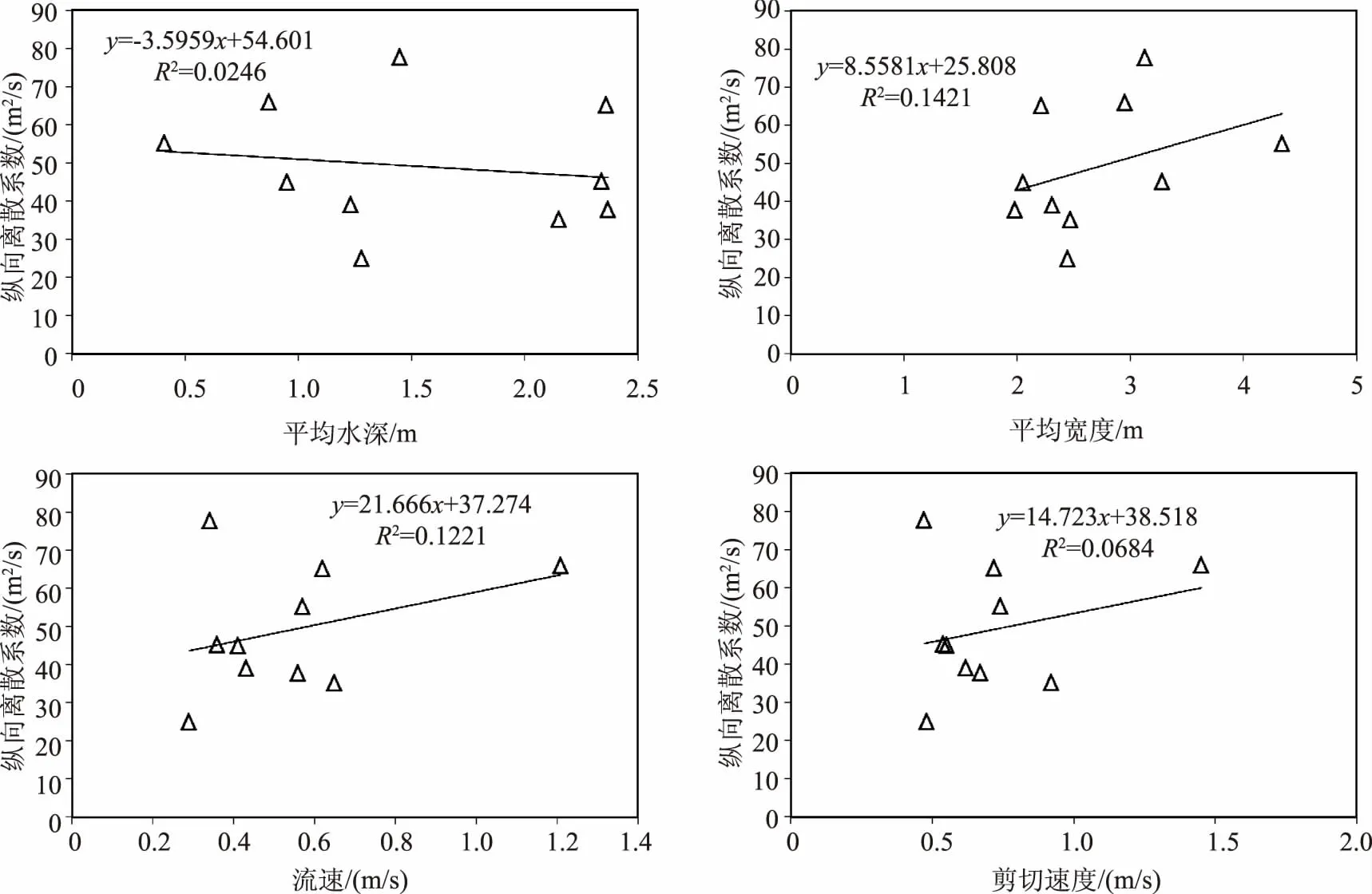
图2 不同变量与纵向离散系数Ex相关敏感度

采样编号W/mν/(m/s)ν*/(m/s)Ex/(m2/s)均方差σ/(m2/s)试验值传统改进传统改进①3.280.360.5438.951.245.22.420.35②2.310.430.6244.664.938.98.340.74③4.340.570.7448.523.555.20.431.21④2.470.650.9224.842.535.18.210.89⑤2.951.211.4572.154.765.99.661.53⑥3.130.340.4783.564.677.52.722.47⑦2.450.290.4822.132.924.91.840.79⑧1.980.560.6744.522.537.82.950.82⑨2.210.620.7261.278.465.24.831.34⑩2.050.410.5535.961.544.95.152.22

图3 优化精度特征对比结果

3.3 水槽示踪试验结果分析

为对优化算法的试验精度进行验证，结合水槽示踪试验方式，进行20组试验，试验结果见表3。

水槽示踪试验的目的在于研究改进SVM优化算法在引水明渠纵向离散系数的优化求解精度，从表3中可以看出，经过20组示踪试验后，各组纵向离散系数值得变幅Cv基本在0.35～0.57之间变化。表明各组纵向离散系数值基本稳定变化，也表明改进的SVM优化算法在引水明渠纵向离散系数的适用性。

4 结论

(1)改进SVM算法具有较强的泛化能力，在引水明渠纵向离散系数优化求解上好于传统优化算法，也可拓展用于天然河流纵向离散系数的优化求解上。

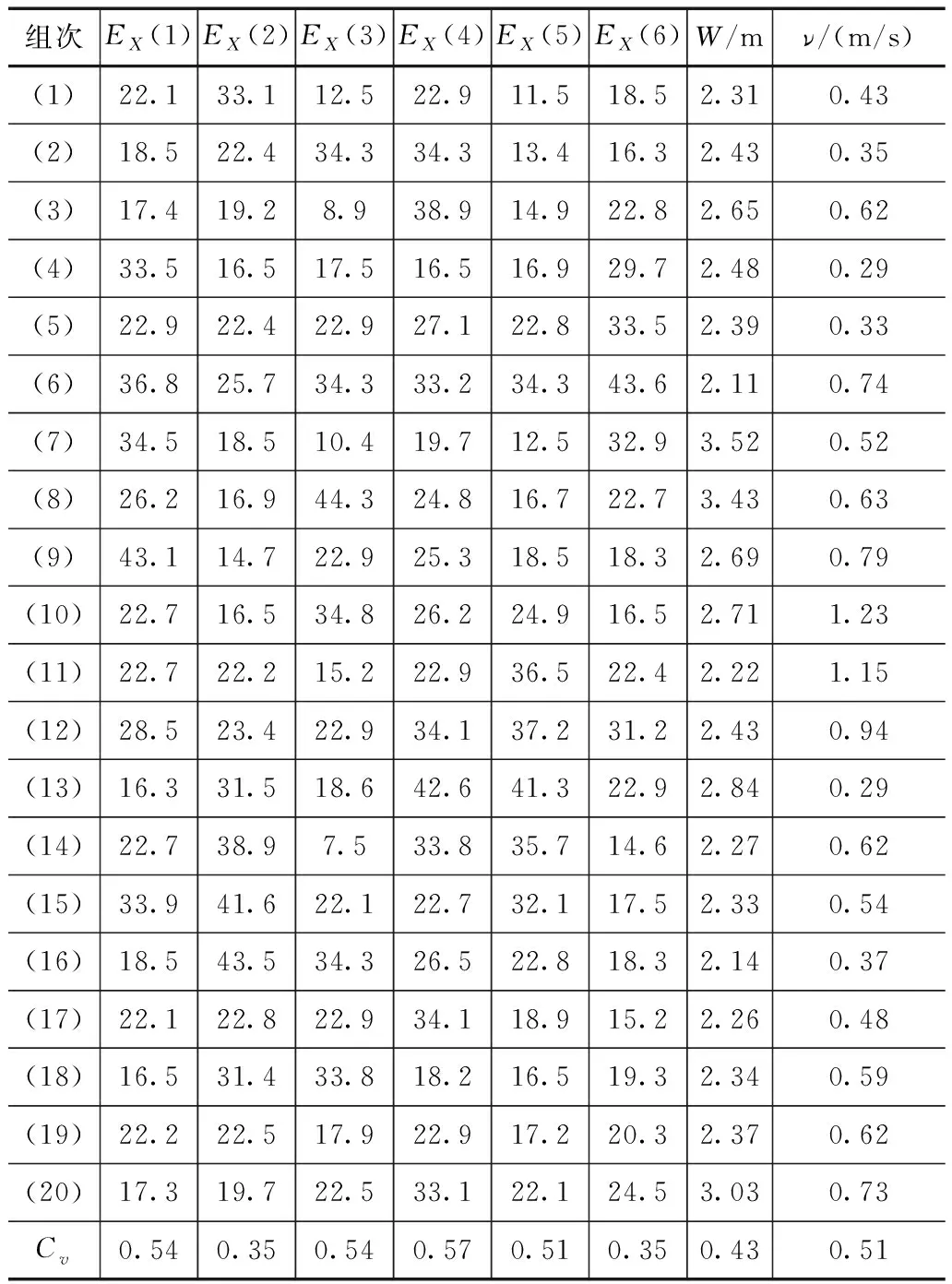
表3 水槽示踪试验结果

(2)文章由于试验条件原因，重点考虑断面形态以及流速等变量对纵向离散系数优化求解的影响，在日后研究中还应加入横断面面积、流量作为纵向离散系数的影响要素进行分析。

[1] 马海波, 崔广柏, 常文娟. 确定河流纵向离散系数的SVM算法[J]. 安徽农业科学, 2010, 38(23): 12630- 12631, 12670.

[2] 庄水英, 姚国富. 天然河流纵向离散系数的计算方法分析[J]. 黑龙江水专学报, 2008, 35(04): 43- 46.

[3] 顾莉, 华祖林, 何伟, 等. 河流污染物纵向离散系数确定的演算优化法[J]. 水利学报, 2007(12): 1421- 1425.

[4] 吴小明, 林芳荣. 用最优化方法计算河流纵向离散系数[J]. 人民珠江, 1993(01): 6- 11.

[5] 周克钊, 余常昭, 张永良. 天然河流纵向离散系数示踪实验计算方法研究[J]. 环境科学学报, 1986(03): 314- 326.

[6] 徐世民, 景淑娟. 基于混沌蚁群算法的SVM模型在水库枯水期径流预测中的应用[J]. 水利技术监督, 2016, 24(06): 99- 102.

[7] 范莹莹. 基于最小二乘支持向量机的河涌水质预测研究[D]. 广东工业大学, 2012.

[8] 苏安俊. 粗糙集理论和Flex技术在中长期径流预报中的应用[D]. 华中科技大学, 2011.

[9] 陈志忠. 基于时间序列组合模型的河川年径流预测[J]. 水利规划与设计, 2016(11): 60- 62, 83.