弹性RBF神经网络在人脸识别中的应用研究

赵文可，孙玉国

（上海理工大学 光电信息与计算机工程学院，上海 200093）

0 引言

随着模式识别领域的不断发展，生物特征识别已经越来越多地应用于身份识别验证领域。人脸识别作为一种模式识别技术，因其识别便捷、识别对象不易伪装，以及对用户的友好性和低侵犯性等特点，在档案管理系统、安全验证系统、信用卡验证、公安系统的罪犯身份识别、银行和海关的监控、人机交互等领域有着重要应用[1]。

径向基函数（Radial Basis Function，RBF）神经网络是一种模仿人类视神经系统的前馈型神经网络，已经被证明对于任意非线性函数都有着良好的逼近能力，解决了BP网络[2-3]容易收敛于局部最优解的问题[4]。其中，RBF神经网络的隐含层作为非线性转换的关键层，模仿了某些生物神经元“内兴奋外抑制”功能。RBF神经网络隐层神经元数、隐层基函数中心、基函数的宽度以及输出权值对网络的学习起关键作用。RBF神经网络的优化问题不但包括隐层神经元数目的增减，还有径向基函数中心、宽度以及输出权值等参数的优化。

本文基于一种弹性 RBF（E-RBF）神经网络结构优化设计方法设计人脸识别系统，该算法基于神经元的活跃度以及神经元修复准则，调整RBF神经网络隐含层神经元的各参数以及隐含层与输出层神经元之间的连接权值，获得一种弹性RBF神经网络[5]。E-RBF神经网络实现了神经网络的结构和参数自校正，具有良好的自适应能力和逼近能力，与其他自组织RBF神将网络相比，在泛化能力、最终网络结构等方面有较大提高。

1 神经元修复准则

神经系统中神经元之间的连接变化分为连接断开和连接加强两种方式，断开时神经元之间不在相互传送信息，加强时相应神经元之间信息传送能力加强[6]。

根据神经元的修复机制，提出如下神经元修复准则：

首先根据香农熵理论，求出神经元X和Y的连接强度为

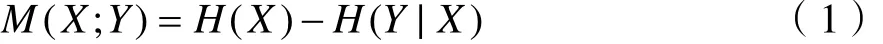
其中， H ( X)为神经元X的香农熵， H ( Y|X)为神经元Y在X条件下的熵[7]。

其次规则化神经元的连接强度：

其中0 ≤ m ( X; Y) ≤ 1，与神经元X和Y的连接强度正相关。

2 E-RBF 神经网络

在设计人脸识别系统时，首先要做的是找出一些最具代表性的特征，然后根据这些特征去进行训练。Karhunen-Loeve变换（简称 K-L）变换，是一种常用的特征提取方法，它以最小均方误差为准则进行数据压缩，是最小均方误差意义下的最优正交变换。

E-RBF神经网络是一种基于神经元的活跃度以及神经元修复准则的RBF神经网络结构优化设计方法，其主要思想为：首先，利用神经元的活跃度函数判断神经元的活跃性，对活跃性较强的神经元进行分裂；其次，利用神经元修复准则计算交互信息相关性函数，分析RBF神经网络隐含层神经元与输出层神经元间的连接强度，根据神经元交互信息强度对网络结构进行修改；最后，对于隐含层神经元，利用快速下降算法对连接权值进行修改，利用梯度下降算法对基函数的中心和方差进行修改[8]。

2.1 神经网络初始化

RBF神经网络结构如图1所示，由一个输入层、一个隐含层和一个输出层组成。本文采用高斯函数作为RBF神经网络的隐含层基函数，设输入层的输入 x ∈Rn，第i个基函数的中心C ∈Rn(i = 1,2,…,m)，

i n为输入层神经元的个数，m为隐含层神经元的个数，输出层的实际输出 Y ∈Rk，k为训练样本类别数，即输出层神经元个数，则隐含层第i个神经元的输出为

式中iσ为第i个基函数的宽度。输出层输出

式中ijw为隐含层第i个神经元与输出层第 j个神经元连接权值。

初始化隐含层神经元个数为输出层神经元个数，计算第 j类样本的均值作为隐含层第 j个基函数的中心，以第 j类样本中距离第 j个基函数的中心的最远距离为基函数的宽度jσ。

图1 RBF 神经网络结构Fig.1 RBF neural network

2.2 神经元分裂

计算隐含层神经元的活跃度：

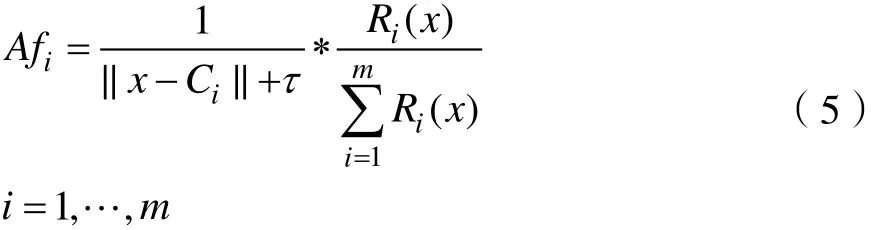
其中，A fi是隐含层第i个神经元的活跃度，τ是为了避免||x - Ci||为零时（5）式无解而设定的一个较小实数值。

设置活跃度阈值 A f0，当 A fi＞Af0时，隐含层第i个神经元为活跃神经元。对活跃神经元进行分裂，新神经元的初始中心及宽度：

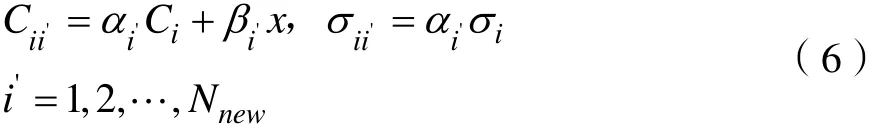
新增神经元个数 Nnew根据第i个神经元的活跃度确定， Cii'和 σii'分别表示第 i'个新增神经元的中心和宽度，αi'∈[0.95,1.05]，βi'∈[0,0.1]。新神经元与输出神经元之间的连接权值：

其中， ri'为第 i'个新增神经元的分配参数，Ri( x)为被分裂的神经元i的输出， Rii'(x)为分裂后的新神经元 i'的输出， wij和 wi'j分别为被分裂神经元和新神经元与第 j个输出层神经元的连接权值，e为神经网络当前误差。

2.3 神经元连接调整

神经元连接调整作用于隐含层神经元和输出层神经元之间。首先计算第i个隐含层神经元和第 j个输入层神经元的交互信息强度 m ( i, j)，并设置交互信息强度阈值γ，如果m( i, j)＞γ，保留神经元之间的连接，如果m( i, j)＜γ，则断开神经元之间的连接，在隐含层中找出与第i个神经元欧氏距离最近的神经元i*，调整神经元 i*参数

2.4 隐含层参数及连接权值调整

设共有N个训练样本，输入矩阵为 X ∈ Rn×N，隐含层的输出矩阵 R ∈ Rm×N，输出层的实际输出矩阵 Y ∈ Rk×N，输出层期望输出 T ∈ Rk×N，权值矩阵W ∈ Rk×m，神经网络逼近误差e = Y - T 。

误差函数定义为

令 Zni( s) = Xn- Ci( s)，根据梯度下降原理，

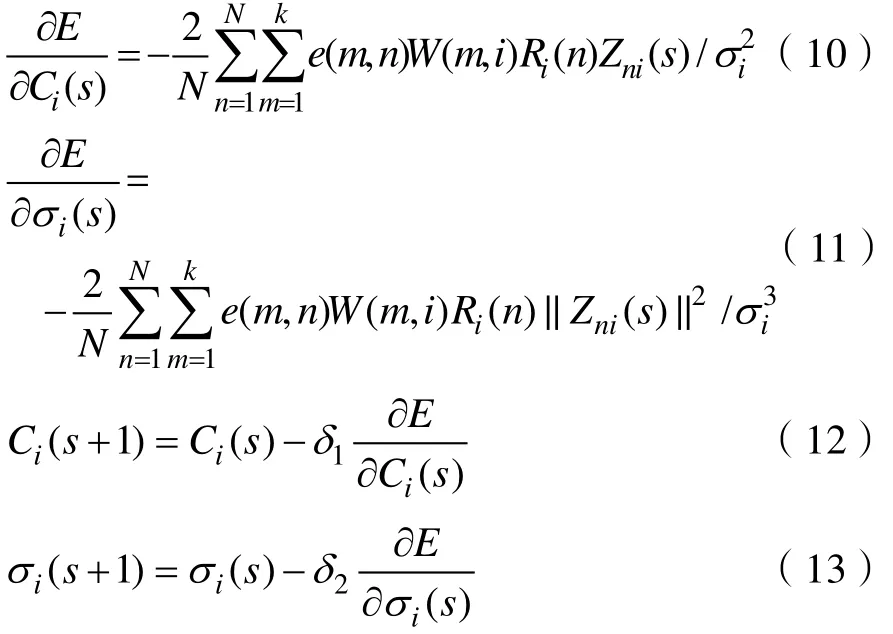
其中，s为迭代次数，101δ＜＜，201δ＜＜，01δ＜＜为参数学习速率，TR为R的转置矩阵，通常基函数宽度的学习速率大于中心的学习速率时，分类器取得较好的性能（一般取212δδ=）。

2.5 E-RBF 神经网络训练流程

基于以上判断和调整，实现对神经网络结构的优化，具体训练过程如下：

搭建RBF神经网络，初始化隐含层单元。

计算神经元的活跃度，并根据活跃度大小判断是否分裂神经元。若分裂，则根据式（7）和式（8）设定新神经元的初始参数。

计算隐含层神经元与输出层神经元之间的连接强度m，如果m大于等于阈值，则跳到步骤（4），否则跳到步骤（5）。

删除该隐含层神经元，在隐含层寻找与原神经元欧氏距离最近的神经元，根据式（11）设定选中神经元的参数。

采用梯度下降算法，调整隐含层神经元的中心值和宽度；采用快速下降算法，调整隐含层与输出层间的连接权值。

满足所有停止条件时停止训练，否则判断结构是否调整结束。结构调整结束则转向步骤（5），否则转向步骤（2）。

3 实验与分析

实验选用 ORL人脸数据库作为实验数据集，ORL人脸数据库共包括40个人，每人10张分辨率为112×92人脸图像样本。图像样本包括表情变化，细微姿态变化，20%以内的尺度变化。

本文首先基于K-L变换对图像数据进行降维处理，提取图像的主要特征，去除数据之间的相关性与冗余性，获得样本数据。之后，随机在每类人脸中选择5张图片作为训练样本，其余5张作为测试样本。采用本文算法进行训练，选择0.01τ=，当选择不同的活跃度阈值0Af时，隐含层神经元个数如表1所示。

表1 活跃度阈值对应的隐含层神经元个数Tab.1 Number of hidden layer neurons and active degree threshold

通过比较各类子训练样本到各自样本中心的最大距离和各子样本中心间的距离，选择活跃度阈值为0.01。以函数误差的变化率小于0.01，迭代次数小于1000为阈值，在学习速率相同的条件下，隐含层神经元和输出层神经元之间信息强度阈值γ与函数误差E的关系如表2所示。

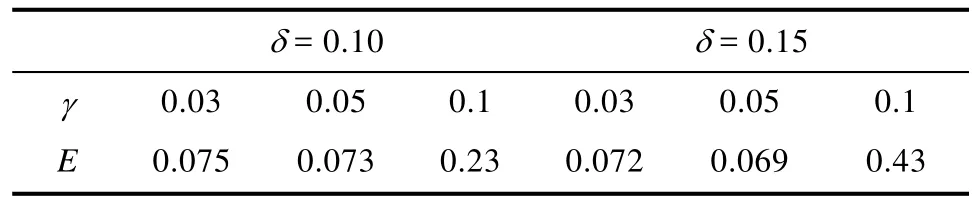
表2 信息强度阈值对函数误差的影响Tab.2 Influence of information intensity threshold on function error

由表2可知，当γ=0.05时，分类器能够取得较好的训练精度。虽然 δ = 0 .15时函数误差较小，但是在训练过程中现了误差反弹现象，在1000次迭代范围内，函数误差的变化率难以收敛到给定阈值。另外，当δ＜0.10时，误差收敛速度明显变慢，在给定阈值条件下的函数误差偏大，所以本文中学习速率选择0.10。误差变化曲线如图2所示。

图2 学习速率为0.10时误差变化曲线Fig.2 Error variation curve when learning rate is 0.10

图3 为某一人脸识别过程，其中，第一行为待识别人脸，第二行为判断待识别人脸所属类别的所有训练样本图片。输入待识别人脸，功能实现确定待识别人脸所属类别，显示属于本类别的所有训练样本图片。

表3为E-RBF神经网络与BP神经网络[9]及传统RBF神经网络的实际训练效果，以训练误差的下降率小于0.01作为阈值。从表中可以看出，从训练时间和识别率上，RBF神经网络都优于BP神经网络，在多次训练时，BP神经网络识别率有3%左右的上下浮动，RBF神经网络则相对稳定。与传统RBF算法相比，E-RBF算法识别效率更高，训练时间更短，从而验证本算法的优越性。

图3 某一识别结果Fig.3 An identification result

表3 三种不同神经网络的实验结果比较Tab.3 Experimental results of different neural networks

4 结论

本文应用弹性RBF神经网络，实现了RBF神经网络的结构和参数自校正，解决了网络结构过大或过小的问题，同时在分类器训练过程中，能够弹性适应同类图像的微小变化，从而提高分类器的识别准确率。

[1] 李武军, 王崇俊, 张炜, 等. 人脸识别研究综述[J].模式识别与人工智能, 2006, (2):58-66.

[2] 张敏, 徐启华. 基于改进BP 的神经网络模型参考自适应控制[J].软件, 2015, 36(7): 118-123

[3] 石黎, 孙志梅. 教学质量评价的BP神经网络模型[J]. 软件,2015, 36(3): 19-21

[4] 张昭昭, 乔俊飞, 余文. 多层自适应模块化神经网络结构设计[J]. 计算机学报, 2017, 40(12): 2827-2838.

[5] 乔俊飞, 韩红桂. 前馈神经网络分析与设计[M]. 北京: 科技出版社, 2013.

[6] GILBERT P M, HAVENSTRITE K L, MAGNUSSON K E G,et al. Substrate elasticity regulates skeletal muscle stem cell self-renewal in culture[J]. Science, 2012, 329(5995):1078-1081.

[7] KRIVOV S, ULANOWICZ R E, DAHIVA A. Quantitative measures of organization for multiagent systems[J]. Bio-systems, 2003, 69(1): 39-54.

[8] KRIVOV S, ULANOWICZ R E, DAHIVA A. Quantitative measures of organization for multiagent systems[J]. Bio-systems, 2003, 69(1): 39-54.

[9] 安大海, 蒋砚军. 基于BP神经网络的人脸识别系统[J]. 软件, 2015, 36(12):76-79.