基于机器学习模型的民航客流预测仿真研究

2018-06-14陈焕东陈明锐

软件 2018年5期

刘夏，邱钊，陈焕东，陈明锐

（1. 三亚航空旅游职业学院人文社科学院，海南三亚 572000；2. 海南大学信息科学技术学院，海南海口 570228；3. 海南师范大学教务处，海南海口 571128）

0 引言

准确地预测机场的旅客客流量，对于机场的运力安排、航线调整以及规划发展有着至关重要的作用。在客流量预测方面，许多学者做了有益尝试。文献[1]采用了Holt-winters模型、ARMA模型、一元回归模型基于近十年的客流预测预测了未来两年的数据，其中ARMA模型的预测精度达96.94%，一元回归模型的预测精度达 99.83%，但是 Holtwinters模型和组合模型精度较差，预测模型仍可改进。文献[2]分别根据时间序列 ARIMA模型和 BP神经网络模型得到的误差平方和，利用单项预测模型权数计算公式计算得到时间序列 ARIMA 模型和BP神经网络模型的权数，在根据组合预测模型的计算公式得到组合预测模型的预测结果，组合预测结果优单项预测结果。文献[3]运用了灰色预测模型预测了2017年某一航线每月的客流量，但是预测结果时序图呈线性趋势，预测精度也仅为87%，预测方法仍可改进。文献[4]运用了ARMA模型、灰色预测GM(1,1)模型、ARMA改进回归模型进行了数据拟合仿真。经实证分析，结果表明：三个模型的平均绝对百分误差分别为 4.19%，4.20%，1.97%，预测精度较高。文献[5]采用了多元回归模型，通过逐步回归的方法筛选出对物流量预测的主要因素，并基于时间序列模型进行拟合并对江苏省未来十年的物流量进行预测，虽然拟合优度达99.99%，但是对于长期的预测仍然存在不确定性。文献[6]分别采用了多元回归模型和基于 ARIMA的时间序列模型对人口进行了预测，经与真实值对比，发现多元回归模型的预测精度较高，但是对变量的处理又会造成共线性或异方差等情况，方法仍可改进。文献[7]首先建立了农药和时间的回归模型，然后对时间序列的非白噪声建立ARMA模型，预测精度有所提高，但是不适用于长时间序列预测。文献[8]运用多元回归分析建立了旅客吞吐量模型，通过逐步回归剔除了不相关因素后对旅客年吞吐量进行了预测，结果显示，平均相对误差仅为2.49 %，精度较高。但因数据只是基于统计年鉴数据，没有预测到每月的旅客吞吐量。文献[9]基于ARIMA模型对时间序列进行回归分析，通过建立的一元线性回归方程来提高预测精度，但是其一元线性回归方程的变量仅为年份，较之多元线性回归方程用于预测精度较差。文献[10]分别用SPSS和MATLAB建立GM(1,1)模型和多元线性回归模型对未来的入境客流进行了预测，预测结果表明，GM 模型精度高于多元线性回归模型，但是单一模型预测仍欠缺说服力，预测精度仍可改进。文献[11]运用SPSS对安徽省入境游客人数在经过二次差分的基础上剔除了趋势影响因素，确立了预测模型在对并对未来的人数进行了预测，但是结果显示短期内的精度较好，长期预测误差加大，模型有待改进。文献[12]先通过指数合成的进行协整检验和格兰杰因果分析，在基于合成指数预测模型开展旅游收入预测，其精度提高了32.42%。文献[13]通过多元线性回归模型和时间序列模型对首都机场2012年-2016年的客流量进行了预测，并在此基础上采用加权的方式进行组合预测，但是权重各占50%的则显得说服力不够。文献[14]运用ARIMA模型预测客流吞吐量的线性部分，再用 BP神经网络对 ARIMA模型的残差进行修正，得到非先行特征趋势后将ARIMA模型的结果和BP模型的的结果进行组合，预测误差值仅为 2.12%。但是该模型仅是对已有数据的验证，并没有预测未来的数据。文献[15]通过利用灰色模型，利用2007~2012年的旅游人数数据，对2013、2014年旅游人数进行了预测，然后建立 GM(1,1)模型，运用移动平均趋势剔除法去除季节影响，对季度城镇旅游人口进行预测，预测值与实际值较好的吻合，并依此对2013和2014年季度城镇旅游人口进行预估。文献[16]介绍了BP神经网络和SVM算法的分类原理，结合两个算法特点，给出层次分类法并做为今后研究方向。文献[17]基于遗传算法(GA)优化的最小二乘支持向量机(LSSVM)的MBR膜通量预测算法，通过对比预测结果和实验数据，得出该算法预测精度高。文献[18]的预测模型可以达到预期结果，对短时流量的预测精度和性能都有所提高。文献[19]对深度学习技术进行了综述，概述了CNN、RNN、LSTM的应用特点和场景。

1 变量选择及数据来源

本文选取了某航空公司2010年至2016年北京到三亚航线每天的客流量的数据作为实证分析，数据包括旅客数等在内的8个变量，将旅客数作为被解释变量，其他的变量均作为解释变量，如表1所示。

表1 衡量指标、变量及符号Tab.1 Measurement index, variable and symbol

2 基于多元回归模型建立与预测

2.1 模型建立

回归分析是处理变量与变量之间关系的一种最为常用的统计分析方法，应用非常的广泛。它的主要目的是研究被解释变量与解释变量之间的数量关系。本文根据选取的变量建立了多元回归模型，其模型的表达式为：

其中tε是随机误差项，利用R软件，对数据进行回归分析得到表2所示。

表2 回归分析结果Tab.2 Regr ession analysis result

根据表 2，可得回归方程的 F检验的统计量为718.2大于 0.05显著水平的临界值，说明回归方程的总体是显著的。对回归方程进行多重共线性检验，得到的结果如表3所示。

表3 相关系数矩阵Tab. 3 Correlation coefficient matrix

根据表3可得，在0.05的显著水平下，解释变量之间存在高度相关性，例如：架次和飞行时间之间的相关性达到0.997，说明上述建立的回归方程存在多重共线性，采用逐步回归建立回归模型，得到的结果如表4所示。

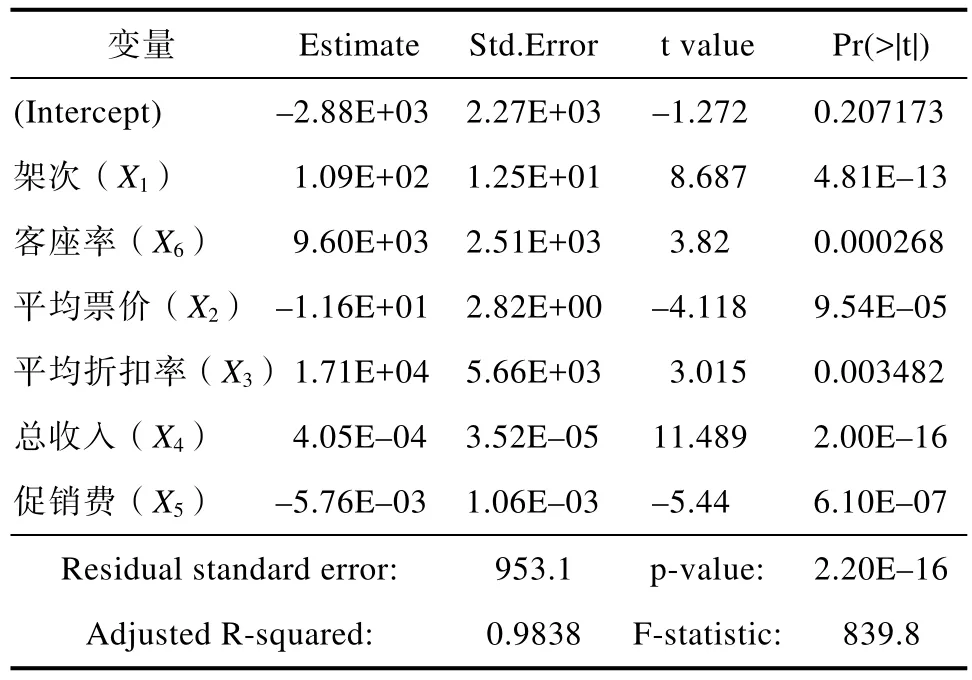
表4 逐步回归结果Tab.4 Result of stepwise regression

根据表4可以得出整个回归方程的检验的P值为 0.0000也是显著地，并且调整后的拟合优度值= 0 .9838，说明方程的拟合效果非常好。因此，建立的回归方程为：

2.2 模型预测

利用上述建立的回归模型对2010至2016年的北京到三亚的客流量进行预测，得到的结果如图1所示。

图1 回归模型的预测时序图Fig.1 Forecasting time sequence chart of the regression model

根据图 1，可得上述回归模型能够很好的预测样本周期内的旅客量的变化，计算回归模型预测的平均绝对误差 M PAE= 5 .27%。

3 基于支持向量机回归（SVR）模型建立与预测

3.1 模型建立

本文选取了平均票价，平均折扣率，总收入，促销费和客座率作为旅客量的特征属性，利用R3.2.3软件，并通过调用 e1071软件包，对北京到三亚航线旅客量进行预测得到的结果如表5所示。

表5 SVR 模型的最优参数Tab.5 Optimal parameters of SVR model

根据表5可得，SVR模型采用径向基核函数，得到的相关最优参数为：模型的约束违反成本 c =1，径向基核函数中的gamma函数因子为 g = 0 .2，估计误差ε=0.1，支持向量机的个数为57个，预测的客流量的平均绝对百分误差为 M APE= 7 .61%。

3.2 模型预测

利用上述建立的支持向量机模型对 2010至2016年的北京到三亚的客流量进行预测，得到的结果如图2所示。

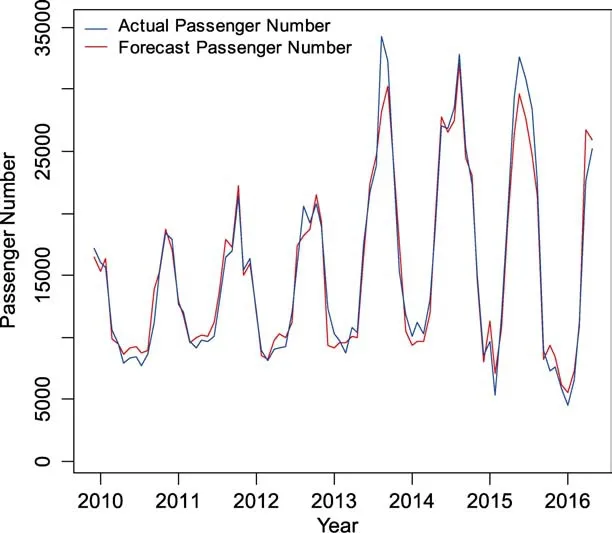
图2 支持向量机回归预测时序图Fig.2 Forecasting time sequence chart of support vector regression

根据图2可得上述支持向量机能够较好的预测样本周期内的旅客量的变化，计算出支持向量机回归预测的平均绝对误差 M PAE= 7 .61%。

4 基于残差检验

对上述两个模型的残差进行检验，观察其是否服从白噪声序列。对上述残差进行稳定性检验，得到的结果如表6所示。

表6 稳定性检验Tab.6 S tability Test

根据表6可得多元回归模型和支持向量机回归模型的残差均是原序列平稳。然后利用R画出多元回归ACF和PACF图如图3所示。

图3 多元回归残差的PACF和ACF图Fig.3 PACF and ACF chart of multi-variable regression residuals

根据图 3可得多元回归模型残差的 ACF和PACF图均在一个标准差之内，说明多元回归模型的残差是白噪声序列。作出支持向量机回归残差的ACF和PACF图，得到的结果如图4所示。

根据图 4可得支持向量机回归残差存在自相关，需对支持向量机模型的残差建立ARMA模型，才能进行预测。

5 基于ARMA改进模型预测

根据图4建立ARMA(28,28)对支持向量机回归模型的残差进行预测，得到的结果如表7所示。

图4 SVR 的PACF和ACF图Fig.4 PACF chart and ACF chart of SVR

表7 SVR 残差的ARMA(28,28)的回归结果Tab.7 Regression result of ARMA (28,28)of SVR residuals

根据表7建立的ARMA(28,28)模型对上述支持向量机模型的残差进行预测，得到的结果如图5所示。

根据图5可得建立的ARMA模型能够较好的拟合 SVR模型的残差，下面利用建立的 SVR和ARMA(28,28)对样本周期内的旅客量进行组合预测。得到的结果如图6所示。

根据图6可得组合预测能够很好的预测样本内旅客数，得到 M APE= 5 .07%，比较各个模型预测误差，得到的结果如表8所示。

根据表8可得组合模型的预测效果在三种模型中是最佳的，超过了回归模型的预测效果，且预测误差很小。因此，支持向量机回归和ARMA模型的组合预测效果较好，能够很好的预测出航线的旅客量，如图7所示。

图5 SVR 残差预测图Fig.5 Forecasting chart of SVR residual

图6 组合预测时序图Fig.6 Time sequence chart of combined forecasting

表8 各个模型的平均绝对误差Tab.8 Average absolute error of various models

6 基于神经网络（RBF）模型鉴于与预测

本文选取了平均票价，平均折扣率，总收入，促销费和客座率作为旅客量的特征属性，对北京到三亚航线旅客量进行预测。利用 caret包中的 train函数确定合适的隐藏层节点数和权重衰减参数decay，得到结果如表9所示。

根据表9可得，结合标准误差最小原则，调整后的拟合优度值最大原则，确定神经网络最佳隐藏节点数为4，decay为0.5。建立神经网络模型来预测样本周期内的旅客数，得到的结果如图8所示。

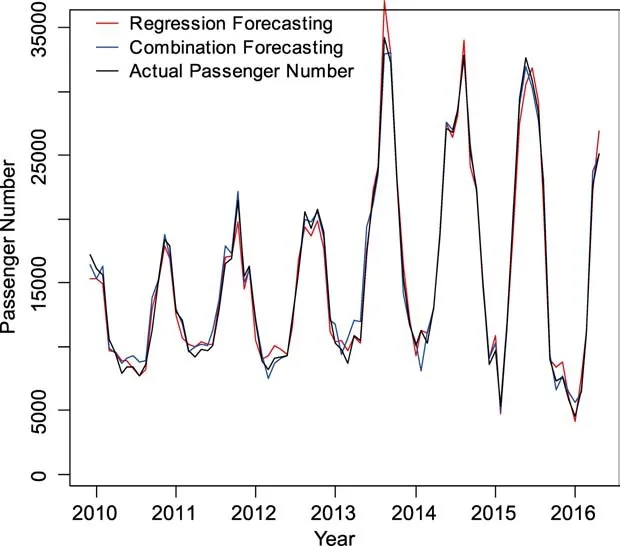
图7 组合模型的预测图Fig.7 Forecasting chart of the combined model

表9 神经网络参数Tab.9 Ne ural network parameters

图8 神经网络预测时序图Fig.8 Time sequence chart of neural network forecasting

根据图8可得神经网络预测能够很好的预测样本内旅客数，得到 M APE= 3 .34%，下面比较各个模型预测误差，得到的结果如表10所示。

表10 各个模型预测平均绝对误差Tab.10 Average absolute error of forecasting by various models

根据表10可得在三种模型的预测中，神经预测效果最佳，其次是回归模型，支持向量机模型预测效果相对较差，上述3个模型均能够很好的预测出航线的旅客量，作出三个模型的预测与真实旅客量的时序图，结果如图9所示。

图9 模型预测时序图Fig.9 For ecasting time sequence chart of the models

7 结论

综上所述，四种模型在预测效果均较好，平均绝对百分误差均小于10。回归模型是传统的统计方法，拥有良好的预测能力，但是受到多重共线性等一些理论假设的限制较多。而支持向量机和神经网络模型均是机器学习方法，具有良好的学习和泛化能力。支持向量机对于小样本的学习能力能力强，泛化能力好。RBF神经网络收敛速度较快。并且随着基于RBF神经网络的在线学习算法及结构优化方法的不断的提出，使得RBF 神经网络比较适用于于大样本集的在线预测系统。而对于对实时性要求相对不高的预测系统。

深度学习是建立、模拟人脑分析学习的神经网络、模仿人脑机制进行数据的解释，是将原始数据通过一些简单的飞先行模型变为更高层次的的表达，其学习特征对数据结构几乎没有什么要求，只要数据足够大时能自学习，深度学习就能发挥其效用。此外，该算法在语音识别系统中已得到广泛的应用，几乎能完全一致地将声音文件转换为文字序列。

在后续的研究中，可以考虑使用递归神经网络（Recurrent neural networks，RNN）以及增强型RNN，如LSTM（long short-term memory networks）等。RNN作为众多深度学习算法中能更好地解决序列输入问题的一种，它能同时考虑当前的输入信息，并同时考虑历史信息向量。因此，可以将一段时间内每天的数据作为输入，基于RNN循环处理，预测出每一天航班的信息和前面若干天信息之间的关联性，从而预测出后一天的客流人数等数据。

[1] Liu X., Huang X., Chen L., Qiu Z., Chen M. (2017) Prediction of Passenger Flow at Sanya Airport Based on Combined Methods. In: Zou B., Li M., Wang H., Song X., Xie W.,Lu Z. (eds) Data Science. ICPCSEE 2017. Communications in Computer and Information Science, vol 727. Springer,Singapore.

[2] 翟静, 曹俊. 基于时间序列ARIMA与BP神经网络的组合预测模型[J]. 统计与决策, 2016(4): 29-32.

[3] Xia, L., et al., Prediction for Air Route Passenger Flow Based on a Grey Prediction Model. 2016, IEEE. p. 185-190.

[4] Liu X., Huang X., Chen L., Qiu Z., Chen M. (2017) Prediction for Passenger Flow at the Airport Based on Different Models. In: Chen G., Shen H., Chen M. (eds) Parallel Architecture, Algorithm and Programming. PAAP 2017. Communications in Computer and Information Science, vol 729.Springer, Singapore.

[5] 武进静, 韩兴勇. 基于多元线性回归模型对江苏省物流需求的预测分析[J]. 上海农业学报, 2015(4): 62-68.

[6] 韩绍庭, 周雨欣. 多元线性回归与ARIMA在中国人口预测中的比较研究[J]. 中国管理信息化, 2014(22): 100-103.

[7] 邓泽培, 赵凌. ARMA模型与回归模型在农药用量预测中的应用[J]. 中国农学通报, 2014, 30(31): 304-307.

[8] 黄邦菊, 林俊松, 郑潇雨, 等. 基于多元线性回归分析的民用运输机场旅客吞吐量预测[J]. 数学的实践与认识,2013, 43(4): 172-178.

[9] 郑彦. 对时间序列的ARIMA调整与回归分析——以民航客运统计为例[J]. 齐齐哈尔大学学报(自然科学版), 2010,26(3): 82-85.

[10] 江伟. 桂林市入境旅游客流量的预测研究——基于多元线性回归模型与GM(1, 1)的比较[J]. 时代金融, 2014(32):65-67.

[11] 陈鹏, 吴玲, 宋徽. 基于ARIMA模型的安徽省入境旅游人数预测[J]. 安徽农业大学学报(社会科学版), 2012, 21(1):32-35.

[12] 张斌儒, 黄先开, 刘树林. 基于网络搜索数据的旅游收入预测——以海南省为例[J]. 经济问题探索, 2015(8):154-160.

[13] 陈玉宝, 曾刚. 基于组合预测方法的民航旅客吞吐量预测研究——以首都机场为例[J]. 中国民航大学学报, 2014,32(2): 59-64.

[14] 尧姚, 陶静, 李毅. 基于ARIMA-BP组合模型的民航旅客运输量预测[J]. 计算机技术与发展, 2015, 25(12): 147-151.

[15] 邱亚利. 基于灰色模型的旅游景点人数预测分析[J]. 统计与决策, 2013(17): 114-117.

[16] 王宏涛, 孙剑伟. 基于BP 神经网络和SVM 的分类方法研究[J]. 软件, 2015, 36(11): 96-99