基于小波系数特征和偏最小二乘回归的近红外光谱定量分析

李四海，任 真

(甘肃中医药大学 信息工程学院， 兰州 730000)

当归为伞形科植物当归的干燥根，是中药材。主产于甘肃、四川、云南等地。其中，甘肃为主要产区。阿魏酸是当归的主要活性成分之一，具有抗氧化和清除自由基、抗菌、抗病毒、降血脂等功效。目前，当归中的阿魏酸含量一般通过HPLC法测定[1-2]，但操作程序较为复杂，分析时间长。

近红外光谱技术是一种新型的分析检测技术。其主要特点是快速、简单、无破坏性。已广泛用于食品、药品、农产品检测，石油化工、中药光谱定性及定量分析等领域。在中药近红外光谱定量分析方面，利用近红外光谱仪快速扫描得到中药材的近红外光谱，运用高效液相色谱法测定中药材中主要成分的含量，然后建立近红外光谱和主要成分含量之间的定量分析模型，利用该模型就能够对未知中药材样本中的主要成分含量进行快速检测。近红外光谱定量分析技术主要包括光谱预处理及定量分析模型的建立。在定量模型的建立方面，偏最小二乘回归能够有效解决光谱的多重共线性问题，被广泛用于近红外光谱的定量分析之中，其他常用的方法包括主成分回归、人工神经网络、支持向量机等[3]。

本文首先对当归近红外光谱进行导数运算和正交信号校正预处理，然后利用离散小波变换对预处理后的光谱信号进一步进行压缩，研究分析了小波变换中的最优小波基及分解尺度；利用小波系数特征并结合偏最小二乘回归方法建立了当归中阿魏酸含量的定量分析模型，为当归中阿魏酸含量的快速、无损检测提供一种新的方法。

1 相关理论

1.1 离散小波变换

小波变换是在傅里叶分析的基础上发展起来的。傅里叶变换将信号分解至正弦和余弦正交基空间，小波变换则将信号分解至具有不同尺度和频率的小波空间，二者的不同之处在于采用的基函数不同。小波分析的基本思想是将任意信号表示为小波函数的线性组合，离散小波变换的基本原理如下[4]：

设信号f(t)在Vj空间中的离散采样序列为f(k),k=0,1,2,…,n-1，则Mallat小波分解算法为：

其中cj,k和dj,k分别为信号的低频和高频部分，h(n)和g(n)分别为低通滤波器H和高通滤波器G的系数,且gn=(-1)nh1-n。

小波变换作为一种有效的时频分析技术已被广泛用于近红外光谱的去噪、数据压缩及特征提取中。选择合适的母小波及分解层数，原始光谱信号可以用不同尺度上的小波系数来表征，这些小波系数可以有效区分低频基线漂移、中频有效信号及高频噪声信号[5-6]。

1.2 偏最小二乘回归

偏最小二乘回归(PLSR)是一种多元统计分析方法，是主成分分析和典型相关分析的结合。由于PLSR能有效解决高维变量之间的多重共线性问题，因此在光谱变量选择、光谱定量分析模型的建立方面得到广泛应用[7-9]。

Qcum2=1.0-∏(PRESSa/SSa-1),a=1,2,…,k

2 结果及分析

2.1 阿魏酸含量测定

77个当归样本分别采自甘肃岷县及渭源县。利用Nicolet-6700型近红外光谱仪扫描得到77个样本的近红外光谱，测样方式为积分球漫反射，分辨率为4cm-1，扫描范围：4000 cm1-10000cm-1，扫描次数64次[10]。77个当归样本的近红外光谱如图2(a)所示。

当归中阿魏酸含量通过高效液相色谱法(HPLC)测定，表1给出了训练集及测试集样本中阿魏酸含量的分布情况。

表1 训练集和测试集中阿魏酸含量分布

2.2 导数光谱及正交信号校正

由于扫描得到的近红外光谱信号包含电噪声、样品背景及杂散光等较多的干扰信息，因此首先进行光谱信号的预处理，然后再建立光谱定量模型。目前常用的光谱预处理方法有：光谱平滑、导数光谱、多元散射校正(MSC)、正交信号校正(OSC)。其中，正交信号校正能够滤除与成分含量正交的光谱信息，保留有用信息。导数光谱则能有效消除基线和其他背景的干扰，分辨重叠峰，提高分辨率和灵敏度。

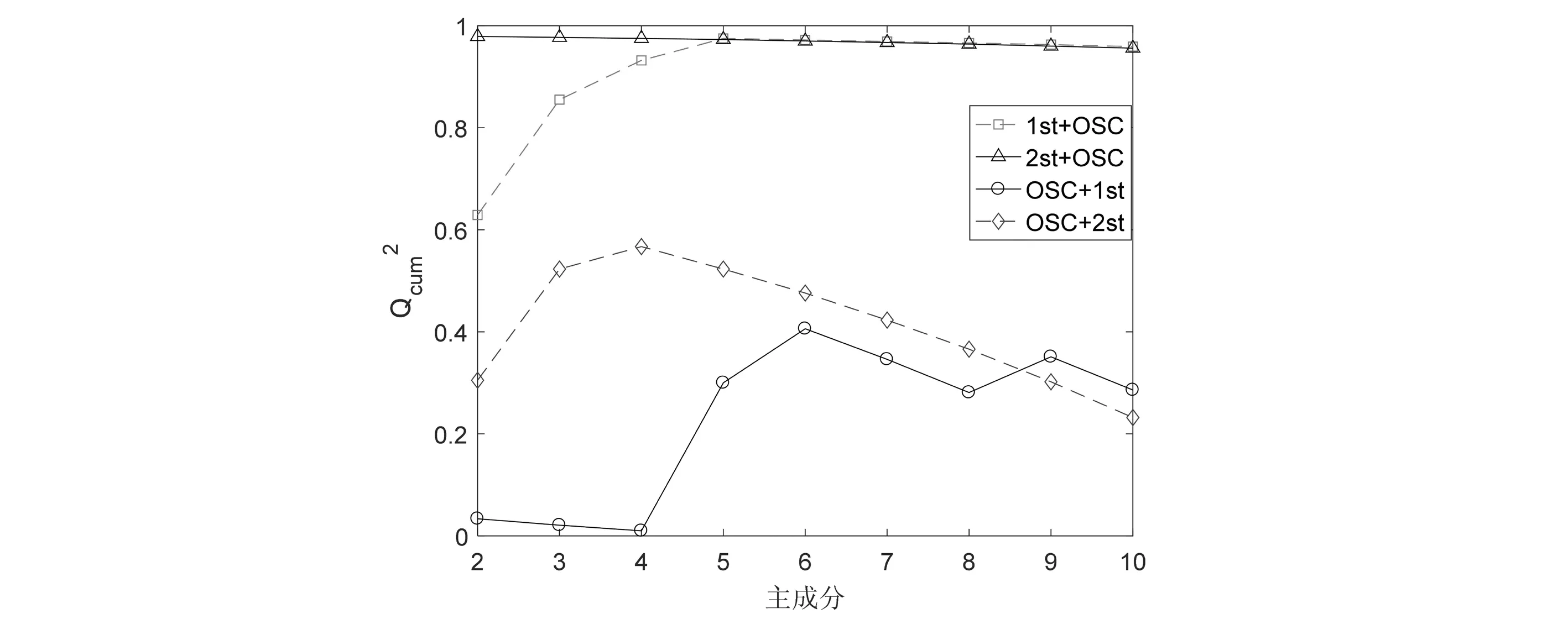
图1 光谱预处理方法对比

2.3 离散小波变换特征提取

由于二阶导数结合正交信号校正预处理后，近红外光谱的维数并没有减少，并且从图2(b)-(c)可以直观地看出，预处理后的光谱仍然包含有一些残存的高频噪声信号。

图2 (a)原始光谱 (b)二阶导数光谱 (c)二阶导数+正交信号校正(d) 二阶导数+正交信号校正+cd4

为进一步对光谱进行压缩并提取有效的光谱特征信息，将预处理后的光谱进行离散小波变换。常用的小波基有Daubechies、Haar、Symlets、Coiflets等，以上小波基均具有正交性、紧支撑性及近似对称性。本文通过实验，最终选用db4小波，分解层数为9。分别使用不同尺度上的小波系数建立阿魏酸含量的偏最小二乘定量分析模型，表2对比了不同尺度上的高频系数所建立的模型性能，其中RMSEE和RMSEP分别为训练集和测试集上的均方根误差。

表2 不同尺度上小波系数的模型性能对比

2.4 阿魏酸定量分析模型的建立

以第4层的小波系数cd4作为当归近红外光谱特征，在57个训练样本上建立当归阿魏酸含量的偏最小二乘定量模型。图3给出了模型对训练样本的拟合效果。可以看出，模型在训练集上的均方根误差(RMSEE)为0.022，交叉验证均方根误差(RMSECV)为0.050，决定系数为0.9909，表明模型对训练样本的拟合效果良好。

使用建立的偏最小二乘模型对20个测试样本中的阿魏酸含量进行预测，表4给出了模型对测试样本的预测结果。从图4可以看出，模型在测试集样本上的决定系数为0.9877，接近于1，预测均方根误差RMSEP为0.042，表明所建立的定量分析模型预测精度高，稳健性好，能够实现当归中阿魏酸含量的快速、准确检测。

图3 模型对训练集的拟合效果 图4 模型在测试集上的预测效果

3 结论

近红外光谱含有的低频背景信号和高频噪声信号会对模型性能产生影响，利用正交信号校正及离散小波变换能够有效剔除无关信号的干扰并实现光谱压缩[12]，为进一步去除光谱中的无关信号，提出了一种链式滤波预处理方法，首先对原始光谱进行二级导数运算，然后再进行正交信号校正及离散小波变换，研究分析了最优小波基及分解层数。根据本文提出的光谱预处理方法建立了当归近红外光谱和阿魏酸含量之间的偏最小二乘分析模型，结果表明，所建立的模型预测精度高、稳健性较好，能够实现当归中阿魏酸含量的快速、无损检测。

参考文献：

[1] 陈超超, 王艳, 梁超. 高效液相色谱法测定当归中阿魏酸的含量[J]. 成都大学学报(自然科学版), 2008, 27(4):284-286.

[2] 申安. 高效液相色谱法测定不同产地当归中阿魏酸的含量[J]. 中医学报, 2015, 30(3):421-422.

[3] 褚小立, 陆婉珍. 近五年我国近红外光谱分析技术研究与应用进展[J]. 光谱学与光谱分析, 2014, 34(10):2595-2605.

[4] 李四海, 魏邦龙, 李爱英. 基于小波神经网络的空气污染指数预报[J]. 长春大学学报, 2013, 23(2):146-148.

[5] Rossel R A V, Lark R M. Improved analysis and modelling of soil diffuse reflectance spectra using wavelets[J]. European Journal of Soil Science, 2009, 60(3):453-464.

[6] 田高友, 褚小立, 袁洪福. 小波变换-偏最小二乘法用于柴油近红外光谱分析[J]. 计算机与应用化学, 2006, 23(10):000971-974.

[7] 张森,石为人,石欣,等.基于偏最小二乘回归和SVM的水质预测[J].计算机工程与应用,2015,51(15):249-254.

[8] Geladi P, Kowalski B R. Partial least-squares regression: a tutorial[J]. Analytica Chimica Acta, 1986, 185(86):1-17.

[9] Mehmood T, Liland K H, Snipen L, et al. A review of variable selection methods in Partial Least Squares Regression[J]. Chemometrics & Intelligent Laboratory Systems, 2012, 118(16):62-69.

[10] 李四海, 陈建国, 任国瑾. 近红外光谱技术快速测定当归中藁本内酯含量[J]. 传感器与微系统, 2017,36(12):114-117.

[11] 田高友, 袁洪福, 刘慧颖,等. 小波变换用于近红外光谱性质分析[J]. 分析化学, 2004, 32(9):1125-1130.

[12] Tavassoli N, Tsai W, Bicho P, et al. Multivariate classification of pulp NIR spectra for end-product properties using discrete wavelet transform with orthogonal signal correction[J]. Analytical Methods, 2014, 6(22):8906-8914.