装备平行仿真中演化建模框架研究*

葛承垄，朱元昌，邸彦强，胡志伟

（陆军工程大学石家庄校区，石家庄 050003）

0 引言

装备平行仿真技术是近年来军用仿真领域的新兴技术，不少国内仿真专家和学者提及装备平行仿真技术的基本思想［1］并提出具体应用设想，已经成为军用仿真领域的研究热点［2］，然而少有文献明确给出装备平行仿真的技术框架，可参考文献等已有成果寥寥无几。从装备作战指挥决策领域和装备维修保障领域对军用仿真技术的新需求出发介绍装备平行仿真技术的概念。

在装备作战指挥决策领域中，作战辅助决策系统采用固定的计算模型，不能根据战场态势进行模型自适应调整，影响指挥决策的准确性，利用仿真系统预测战场态势并为指挥员提供实时决策支持成为指挥控制系统的发展趋势［3］。在装备维修保障领域中，故障预测与健康管理（Prognostic and Health Management，PHM）技术是实现装备视情维修的主要技术途径，其中装备剩余寿命（Remaining Useful Life，RUL）预测是 PHM［4］的主要研究内容之一。现有RUL预测方法大都是离线预测方法，且预测模型无法根据装备信息进行模型更新，不具备自适应能力，使得RUL预测的时效性差、准确度不高，利用实时退化数据演化预测模型，实现具有自更新能力的RUL预测成为解决这些问题的有效途径［5］。

以上两个装备运用领域中遇到的突出问题可以归纳为领域模型固定，不具备自适应演化能力，要求研究具有模型演化能力的军用仿真技术即装备平行仿真技术。文献［6-7］提出了装备平行仿真技术的概念和技术内涵，装备平行仿真技术是指实际武器装备和平行仿真系统通过特定的接口设备连接在一起，平行仿真系统通过传感器等设备以在线的方式实时获取装备信息，用于演化装备参考模型，提高仿真结果的可信度，仿真结果通过执行器反馈给实际武器装备，从而提高武器装备的运用效能和保障效能。装备平行仿真示意图如图1所示。在空间上，实际武器装备和与之对应的平行仿真系统构成装备平行系统，二者之间是双向交互、互利共生的关系。装备平行仿真可用于装备指挥决策和维修保障等领域中，解决领域模型固定、不具备自适应演化能力这一问题。装备平行仿真的理论缘起与平行系统理论［8］、共生仿真［9］、在线仿真［10］和动态数据驱动应用系统（Dynamic Data Driven Application System，DDDAS）［11］等理论范式密切相关，文献［7］已作详细评述。作为新兴仿真技术，装备平行仿真具有虚实共生、双向交互、模型演化、高效运行等特点，其中模型演化是其在建模方法上区别于以往仿真技术的主要所在，但是至今仍缺乏完整的技术框架。

图1 装备平行仿真示意图

1 装备平行仿真中的演化建模问题

1.1 装备平行仿真中的仿真模型与模型演化

利用不同的建模方式可以得到刻画装备不同特性的模型，设集合M为所有可用于描述装备特性的模型集，Θ为当前时刻的仿真模型。随着装备状态、行为的变化，为提高平行仿真系统的仿真可信度，需要根据当前装备状态和行为信息演化当前模型Θ，以适应装备状态和行为的变化。对于特定的仿真应用和装备状态来说，存在适宜模型集以高逼真度仿真实际武器装备的特定状态和行为，称此模型集为参考模型集MR，有，是否成立取决于时间，随着装备运行状态和行为的变化，平行仿真系统需要对Θ进行演化修正甚至模型更替，当前模型的演化修正、新模型加入和旧模型剔除使得MR是时变模型集。模型演化并没有严格定义，参考已成熟的软件动态演化的概念［12］，本文认为装备平行仿真中的模型演化是指平行仿真系统为适应动态变化的装备状态、满足不断变化的仿真需求而对仿真模型进行的自适应调整，并从仿真模型的一般组成对模型演化进行细化。一般来讲，完整的仿真模型Θ由模型输入input、模型参数模型输出output构成，特定建模方式下三者的组合决定了模型结构，如图2所示。故模型演化可以分为模型输入演化、模型参数演化、模型输出演化和模型结构演化，模型输入演化是指减少模型的冗余输入［13］，以优化模型结构；模型参数演化是指模型参数的更新/优化［14］；模型输出演化是指模型输出的自适应校正［15］；模型结构演化是指模型的适宜性选择/动态更替［16］。由于在特定仿真应用中，模型输入的数据源往往是固定的，因此，这里仅考虑模型参数演化、模型输出校正和模型适宜性选择。本文主要关注面向装备RUL预测的平行仿真中演化建模问题。

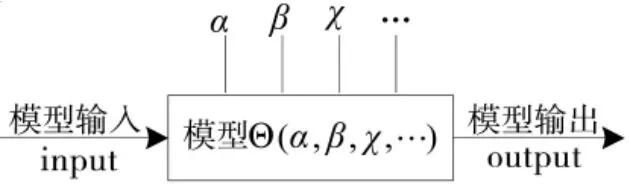
图2 仿真模型的一般表示示意图

1.2 面向装备RUL预测的平行仿真中演化建模框架

装备平行仿真中的仿真模型是能够反映装备某一特性的模型，不同种类的装备平行仿真中模型的内涵不同，在面向装备RUL预测的平行仿真中首先应该解决仿真模型定位即基础预测模型的问题。

1.2.1 基础预测模型

仿真模型是仿真执行的基础，面向装备RUL预测的平行仿真中仿真模型属于预测模型。受装备复杂度和装备运行环境等的影响，实际武器装备状态具有明显的不确定性、时变性和动态性，因此，实际武器装备可以看作动态系统。实际武器装备由正常工作到发生功能性故障的过程是性能逐渐退化的过程，且描述动态系统常用的方法是建立系统的状态空间模型（State Space Model，SSM），所以基于SSM的装备性能退化建模是面向装备RUL预测的平行仿真中的建模方向。SSM的一般形式包括状态方程和观测方程，即

其中，xk为状态变量，zk为外界观测，和分别是均值为0、（协）方差为Qk-1和Rk且相互独立的过程噪声和观测噪声，为有界映射。

1.2.2 演化建模框架

面向装备RUL预测的平行仿真中演化建模框架如图3所示，模型演化主要包括3个阶段：首先，平行仿真系统根据装备实时退化状态和模型在线选择算法从模型库中在线选择适宜装备退化SSM，作为RUL基础预测模型；其次，平行仿真系统利用数据同化算法对装备退化状态进行跟踪，实现对装备退化SSM的输出校正，得到更为准确的装备退化后验状态；平行仿真系统根据装备当前和历史退化状态，利用参数在线估计算法对预测模型中的未知参数（包括超参数）进行准确实时估计；最后，平行仿真系统利用演化后的装备退化SSM，结合装备失效阈值，外推装备退化状态到达失效阈值的时间，并经过多次Monte-Carlo仿真得到装备RUL及其概率密度函数。

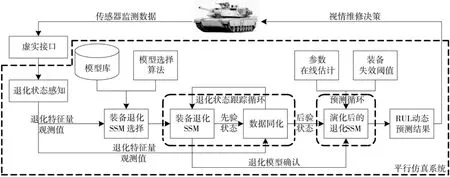
图3 面向装备RUL预测的平行仿真中演化建模框架

面向装备RUL预测的平行仿真中演化建模是一种装备退化数据驱动的演化建模，实现装备退化状态的在线、实时、准确感知是完成演化建模的前提。装备退化状态感知涉及传感器技术、数据预处理技术、虚实接口技术等，在此不作展开讨论，重点研究讨论模型在线适宜性选择技术、数据同化算法和参数在线估计算法。

2 数据驱动的模型在线适宜性选择

与以往仿真技术不同，在装备平行仿真中将模型的验证过程与模型构建过程一同处理，模型的构建确保了仿真模型的可信度。装备平行仿真中的模型构建属于数据驱动的模型构建过程，平行仿真系统能根据装备当前和历史状态数据以在线形式从模型库中调用适宜模型，其本质属于模型适宜性选择过程。装备性能退化过程受复杂工况、人为因素和其他随机因素等的影响，具有时变性强、波动大、多阶段退化等特点，在面向装备RUL预测的平行仿真中，根据装备性能退化轨迹的特征，可以将装备性能退化SSM划分为线性退化SSM和非线性退化SSM，模型适宜性选择指的平行仿真系统根据装备当前和历史性能退化数据从两类退化SSM中动态选择适宜模型。根据平行仿真系统模型输入维数（特征退化量的数量）的不同，提出两种模型适宜性选择方法。

2.1 单维退化数据情况下模型在线适宜性选择

部分装备的性能退化可用单一退化特征量表征，如用漂移特征量表征导弹装备中陀螺仪的性能退化过程［17］、用振动信号的均方根值描述轴承的性能退化过程［18］等。与DDDAS类似，装备平行仿真能将模型构建与模型验证一并处理［19］，因此，可将模型适宜性选择过程看作多仿真模型的在线验证，并提出时频域联合分析方法对装备性能退化SSM进行适宜性选择，即在时域、频域中分别采用灰色关联度分析、最大熵谱估计对仿真模型进行选择。

灰色关联度分析［20］是模型验证领域中的经典时域分析方法，属于几何分析范畴，它通过分析比较仿真模型输出数据和参考数据变化趋势的相似程度即关联度来定量分析二者的一致性，关联度越大，模型越为适宜，反之模型越不适宜。设参考数据序列即装备性能退化真实数据为，并设有m个用于仿真装备性能退化的SSM，第i个仿真模型输出序列为，其中。仿真模型输出序列xi与装备退化数据x0在时刻k处的差异可以表示为

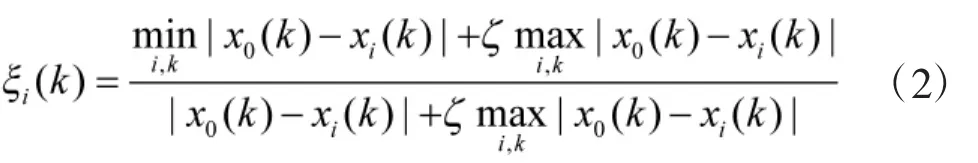
称为关联系数，ζ为分辨系数且，ζ可减小序列极值对二者关联度的影响。xi和x0的关联度定义为

对式（3）取最大值有，关联度最大者对应的模型即为当前退化状态下的适宜SSM。

最大熵谱估计是常用的现代谱估计方法，克服了古典加窗谱分析精度低、能量泄露等不足，能在频域中对仿真模型进行有效验证，具体算法参见文献［21］。利用灰色关联度分析和最大熵谱估计对仿真模型进行适宜性选择，是分别在时域和频域两个不同角度得到的选择结果，存在选择结果冲突的情况，可利用D-S证据理论中冲突理论合成方法对二者的选择结果进行融合［22］，得到最终的仿真模型选择结果。

2.2 多维退化数据情况下模型在线适宜性选择

武器装备性能退化过程的复杂性和不确定性决定了存在表征性能退化过程的多特征量［23］。多特征量问题集中表现在特征量多、特征量间相关，使得特征量之间存在信息重叠、数据维数高。为降低RUL预测的计算复杂度，需对多退化特征量进行数据降维，得到反映原有多退化特征量信息的综合退化特征量。核主成分分析（Kernel Principle Component Analysis，KPCA）是常用的数据降维方法，相较于主成分分析（Principle Component Analysis，PCA）方法，KPCA引入核方法，能够保留更多的原始信息，更适宜处理多维退化数据的特征提取［24］。设高维退化特征量为，定义非线性映射函数用于实现从输入空间向特征空间（再生核Hilbert空间）的变换，即，输入空间样本xb、xc在特征空间中的距离用点积表示，定义核函数K，使得

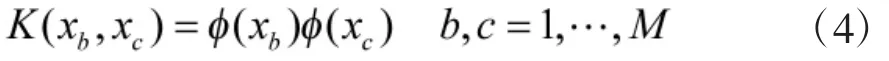
其中，高斯核函数是常用核函数，即

σ为核带宽参数，非线性变换完毕后，在特征空间执行PCA算法得到主成分。模型在线适宜性选择的本质是模式识别问题，即多维退化数据对退化SSM的选择。误差反向传播神经网络（Back Propagation Neural Network，BPNN）是常用的模式识别方法。针对多维退化数据情况下模型在线适宜性选择问题，提出一种基于KPCA和BPNN的模型适宜性选择方法，如图4所示。

首先对M维退化特征量采用KPCA算法得到维相互独立的主成分；L维主成分经归一化处理后，得到BP神经网络的输入，经模式识别后，得到适宜的装备性能退化SSM。模式识别前，需要利用装备性能退化历史数据对BP神经网络进行训练，得到输入层qj和隐藏层yi之间的权值矩阵Wji、隐藏层yi和输出层ol之间的权值矩阵Til，并将最新的识别过程输入输出数据动态加入到神经网络训练数据库中，提高模式识别的准确度。

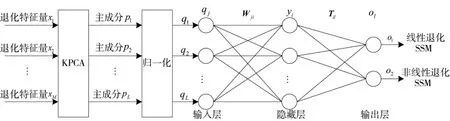
图4 多维退化数据情况下基于KPCA和BP神经网络的模型适宜性选择

3 基于数据同化的模型输出校正

数据同化（Data Assimilation，DA）缘起于数值天气预报（Numerical Weather Prediction，NWP）领域，指模型输出数据与观测数据变得相近的过程［25］，是联系模型预测和观测数据的核心部分。在面向装备RUL预测的平行仿真中，借鉴数据同化的思想，将最新的装备性能退化数据引入装备退化SSM中，利用顺序数据同化算法校正预测模型输出，提高RUL预测精度。顺序DA算法又称滤波算法，常用的算法包括卡尔曼滤波（Kalman Filter，KF）及其改进算法［26］、粒子滤波（Particle Filter，PF）及其改进算法［27］、层次Bayesian方法等，这里结合RUL预测需求重点研究KF和PF算法。

3.1 卡尔曼滤波算法

KF是典型的最小方差估计方法，最优KF问题就是给定装备性能退化数据观测序列，找到性能退化特征量即系统状态 xk+1的最优线性估计，使得估计误差的方差最小。将式（1）具体化，装备性能退化离散状态空间模型可表示为

其中，Fk和Hk是系统矩阵和观测矩阵；状态初值一般取，状态协方差P0可任意假定。

以式（6）为基础预测模型，应用KF算法对装备性能退化过程进行跟踪预测。KF算法分为预测和更新两个步骤：预测阶段利用当前时刻k的状态及其协方差估计Pk|k得到下一时刻k+1二者的先验估计；更新阶段利用k+1时刻最新观测数据zk+1和先验估计得到状态xk+1的后验估计。KF算法可参见文献［26］。

由于KF算法要求SSM是线性模型且w和v为相互独立的高斯白噪声，因此，KF算法适宜于退化过程属于线性高斯的武器装备。为提高KF算法的适用性，国内外学者分别提出了扩展卡尔曼滤波（Extended Kalman Filter，EKF）、集合卡尔曼滤波（Ensemble Kalman Filter，EnKF）、无迹卡尔曼滤波（Unscented Kalman Filter，UKF）等改进方法，不再展开研究。

3.2 粒子滤波算法

实际武器装备退化状态的变化过程大都是非线性的，不适宜应用KF算法，对应的退化SSM是非线性非高斯模型。考虑非线性SSM可表示为式（1），此时和分别是均值为0、协方差为Qk+1和Rk且相互独立的过程噪声和观测噪声，为有界非线性映射。对于非线性非高斯的装备性能退化状态估计问题，以Monte-Carlo方法和序贯重要性采样（Sequential Importance Sampling，SIS）为基础的粒子滤波算法具有较大优势。PF算法通过对来自于装备退化状态概率密度函数的采样集进行预测和更新得到装备退化状态的后验Bayesian估计。PF算法可参见文献［27］。

4 基于参数在线估计的模型参数演化

在式（1）的装备退化SSM中，存在未知参数Q、R，当基于随机过程如Wiener过程、Gamma过程等进行SSM建模时还存在与这些分布相关的超参数，这些参数构成了SSM的未知参数集。平行仿真系统利用模型参数在线估计算法对未知参数集Θ进行在线估计，使得参数值随着装备退化状态的变化进行自适应调整，从而提高装备退化状态预测的准确性，可选的算法包括期望最大化（Expectation Maximization，EM）算法［28-29］、马尔可夫链蒙特卡罗（Markov Chain Monte Carlo，MCMC）方法［30］等。

4.1 期望最大化算法

EM算法是一种迭代算法，主要用于求取后验分布的极大似然估计，能有效估计具有隐含状态SSM中的未知参数，它的每一次迭代由两步组成，即E步（求期望）和M步（极大化）。一般地，以表示Θ的基于装备退化观测数据z的后验分布密度函数，称为观测后验分布，表示添加隐含退化状态x后得到的关于Θ的后验分布密度函数，称为添加后验分布，表示在给定Θ和退化观测数据z下隐含退化状态x的条件分布密度函数。为计算观测后验分布的极大似然估计值，记为第i次迭代开始时的极大似然估计值，则第i+1次迭代的两步为：

E步：将记为关于x的条件分布并求数学期望，从而把隐含退化状态x利用积分运算消掉，即

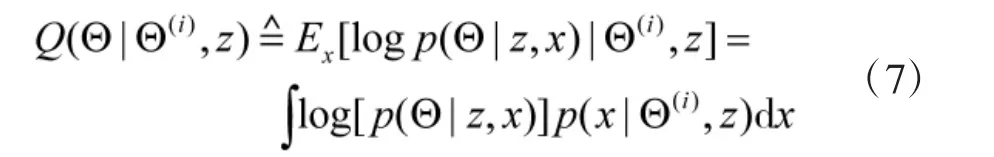
M步：将极大化，即找到新参数，使

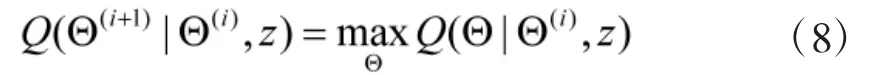
如此形成了一次迭代。将上述E步和M步进行迭代直至或时停止迭代。EM算法能与数据同化算法联合使用，对装备退化状态、参数进行联合估计，即在E步可利用不断更新的装备退化观测数据z和DA算法更新装备退化状态，在M步得到SSM中未知参数的估计值，进而将经模型演化获得的退化状态和SSM未知参数用于RUL预测。

4.2MCMC方法

EM得到是参数后验分布的极大似然估计值，对于Θ的后验均值、后验方差等的获取需要利用MCMC方法，尤其是在多退化特征量情况下，参数集Θ中参数的联合分布是复杂高维且非标准形式的分布，此时EM算法难以实施。

MCMC方法属于统计试验方法，它从一个目标概率分布中抽样，得到收敛、平稳的一定容量样本，由于各个参数的样本值分布近似于其边缘分布，故把各个参数样本值带入定积分近似计算公式中就得到该参数的数字特征。通过MCMC方法可得到参数后验联合分布，在Bayesian框架下，目标概率分布就是参数的后验联合分布。MCMC算法可参见文献［30］。

5 结论

作为新兴军用仿真技术，装备平行仿真能有效满足装备指挥决策领域和维修保障领域中对仿真技术的需求，其中数据驱动的模型演化是其主要技术内涵，通过讨论装备平行仿真中的演化建模问题，明确了演化建模内涵，并建立了面向装备RUL预测的平行仿真中演化建模框架，能实现对装备RUL的实时、在线、自适应预测。

［1］胡晓峰.大数据时代对建模仿真的挑战与思考［J］.军事运筹与系统工程，2013，27（4）：5-12.

［2］李晓婉，窦林涛，程健庆.平行仿真技术在指控系统中的应用构想［C］//2015全国仿真技术学术会议论文集，2015：36-39.

［3］王飞跃.指控5.0：平行时代的智能指挥与控制体系［J］.指挥与控制学报，2015，1（1）：107-120.

［4］SCANFF E，FELDMAN K L，GHELAM S，et al.Life cycle cost impact of using prognostic health management（PHM）for helicopter avionics ［J］.Microelectronics Reliability，2007（47）：1857-1864.

［5］张仕新，昝翔，李浩，等.状态维修理论及剩余寿命预测的研究现状与展望［J］.兵工自动化，2014，33（9）：15-20.

［6］葛承垄，朱元昌，邸彦强，等.装备精确维修平行仿真系统及关键技术研究［J］.现代防御技术，2016，44（6）：162-168.

［7］GE C L，ZHU Y C，DI Y Q，et al.Equipment residual useful life prediction oriented parallel simulation framework［C］//Proceedings of AsiaSim/SCS AutumnSim 2016，Part I，CCIS 643：377-386.

［8］王飞跃.平行控制：数据驱动的计算控制方法［J］.自动化学报，2013，39（4）：293-302.

［9］AYDT H，CAI W，TURNER S J，et al.Symbiotic simulation for optimization oftooloperations in semiconductor manufacturing［C］//Proceedings of the Winter Simulation Conference，2011：2093-2104.

［10］吴金平，陆铭华.指挥控制系统中仿真决策系统的嵌入研究［J］.火力与指挥控制，2015，40（6）：84-87.

［11］DAREMA F.Dynamic data driven applications systems：new capabilities for application simulations and measurements［C］//Proceedings of the International Conference on Computational Science2005， Berlin，Springer-Verlag，2005，LNCS 3515：610-615.

［12］李青山，王璐，褚华，等.一种基于智能体技术的软件自适应动态演化机制［J］.软件学报，2015，26（4）：760-777.

［13］郭俊，周建中，王浩，等.系统理论水文模型结构与参数多目标优化［J］.水力发电学报，2014，33（2）：1-7.

［14］侯景伟，孔云峰，孙九林.蚁群算法在需水预测模型参数优化中的应用［J］.计算机应用，2012，32（10）：2952-2955.

［15］马建文，秦思娴.数据同化算法研究现状综述［J］.地球科学进展，2012，27（7）：747-757.

［16］杨广斌，刘鹏举，唐小明.动态数据驱动的林火蔓延模型适宜性选择［J］.林业科学，2011，47（1）：107-112.

［17］冯磊，王宏力，周志杰，等.基于状态空间的惯性测量组合剩余寿命在线预测［J］.清华大学学报（自然科学版），2014，54（4）：508-514.

［18］MORTADA M.Diagnosis of rotor bearings using logical analysis of data ［J］.Journal of Quality in Maintenance Engineering，2011，17（4）：371-397.

［19］周云，黄柯棣，胡德文.动态数据驱动应用系统的概念研究［J］.系统仿真学报，2009，21（8）：2138-2141.

［20］宁小磊，吴颖霞，于天明，等.基于改进灰色关联分析的仿真模型综合验证方法［J］.兵工学报，2016，37（2）：338-347.

［21］王建华，符文星，董敏周，等.最大熵谱估计在空空导弹仿真模型验证中的应用［J］.弹箭与制导学报，2005，25（4）：848-850.

［22］张鑫，牟龙华.基于局部冲突消除的证据合成法则［J］.系统工程与电子技术，2016，38（7）：1594-1599.

［23］王小林，郭波，程志君.基于非线性漂移Wiener过程的产品实时可靠性评估［J］.中南大学学报，2013，44（8）：3203-3209.

［24］SCHOLKOPF B，SMOLA A J，MULLER K R.Nonlinear component analysis as a kernel eigenvalue problem［J］.Neural Computation，1998，10（5）：1299-1319.

［25］RODELL M，HOUSER P R，JAMBOR U，et al.The global land data assimilation system ［J］.Bulletin of the American Meteorological Society，2004，85（3）：381-394.

［26］REICHLE R H，WALKER J P，KOSTER R D，et al.Extended versus ensemble Kalman filtering for land data assimilation［J］.Journal of Hydrometeorology，2002，3（6）：728-740.

［27］毕海芸，马建文.粒子滤波算法在数据同化中的应用研究进展［J］.遥感技术与应用，2014，29（5）：701-710.

［28］茆诗松，王静龙，濮晓龙.高等数理统计［M］.北京：高等教育出版社，1998.

［29］DEMPSTER A P，LAIRD N M，RUBIN D B.Maximum likelihood from incomplete data via the EM algorithm［J］.Journal of the Royal Statistical Society：Series B，1977，39（1）：1-38.

［30］王浩伟，徐廷学，刘勇.基于随机参数Gamma过程的剩余寿命预测方法［J］.浙江大学学报（工学版），2015，49（4）：699-704，762.