悬吊式静力试验应变测量数据快速处理方法

刘斯以，王 崇，张俊愿

(中国直升机设计研究所，江西 景德镇 333001)

0 引言

直升机的全机或部件结构静力试验是研究全机或部件结构在静载荷作用下的静强度特性，用以检验结构能否满足设计和强度规范要求的一种方法，是直升机研制过程中不可缺少的重要环节[1]。在直升机悬吊件静力试验中，试验件结构重量、假件重量、加载设备及测试设备重量等因素若无法通过传力设备消除，在零载荷时，试验件存在内应力，将引起试验测量应变零点值偏移，测量零点的偏移将对以后每级载荷的试验数据的真实性造成影响[2，3]。为提高试验数据的真实性，研究其试验测量值的数据处理方法用以修正试验数据具有重要意义。

1 悬吊模式及载荷分布

1.1 悬吊模式

外悬吊根据悬吊方向通常分为下悬吊、侧悬吊两种模式，侧悬吊又可分左侧悬吊和右侧悬吊。按悬挂方向分类的悬吊模式示意图见图1。下悬吊根据悬吊点的数量，又可分为单点悬吊和多点悬吊。按悬吊点数量分类的悬吊模式示意图见图2。

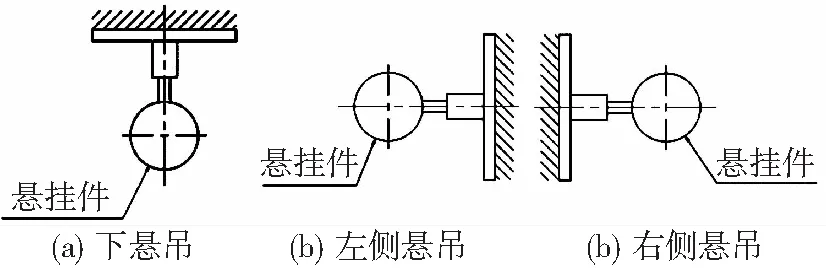
图1 按悬吊方向分类的悬吊模式示意图

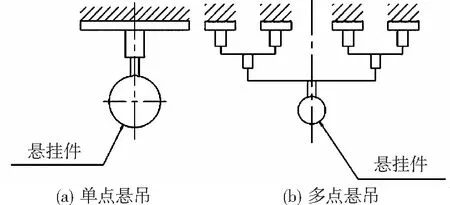
图2 按悬吊点数量分类的悬吊模式示意图

1.2 分布载荷

将载荷分布在线、面、体上的即为分布载荷，对应的分别为线性分布载荷、面载荷、体载荷。对于悬吊件，分布载荷指载荷按一定规律分布于悬吊件空间、坐标平面或坐标轴线上各点。以悬吊件所受力为例，若悬吊件是一长度为L、半径为r的圆柱体，图3(b)所示是圆柱体上载荷沿坐标轴线连续分布的示意图。图中圆柱体上X、Y、Z向所受力分别作用于X、Y和Z轴线上各坐标点，其大小为：fX=f(y)、fY=f(z)和fZ=f(y)。为便于讨论，常将分布载荷简化为悬吊件质点所受作用力与力矩，如图3(a)所示。此外，载荷的分布可以是连续分布，也常有离散点分布，如图3(c)所示[4]。

2 悬吊件的试验加载控制模式

在悬吊式静力试验中，由于试验件自身的重量和参试设施的重量，在实际加载过程中这些重量是作为载荷存在，在加载过程中需扣除这些重量带来的载荷，只有当某一级某点的载荷超过该加载点分配重量时该点才需要加载。实际试验中在零级载荷下所测得的零点为在垂向载荷作用下所对应的数据，并非试验件在零载荷下的真实值，而是包含了自重引起的内应力。因此所测试验数据存在零点偏移的情况，需对该情况进行数据修正以还原试验件实际受力的真实应力状态。

3 悬吊式静力试验应变测量结果及数据处理

3.1 应变测试结果

某型直升机全机静力试验是一种典型的悬吊式静力试验。在对称俯冲拉起工况中，采用加载作动器施加载荷，粘贴应变片测量应变数据。其中选取4个应变测量点，测点编号分别为1#、2#、3#、4#。静力试验加载方式通常载荷级数为0%，10%，20%，30%，35%…60%，67%，70%，75%，…，100%，每级以不大于10%递增至30%，再以5%递增至60%，后增至67%，之后以不大于5%递增至设计载荷。原始测量应变数据如表1所示。将载荷级数与4个测点的应变数据分别作图，如图4所示。

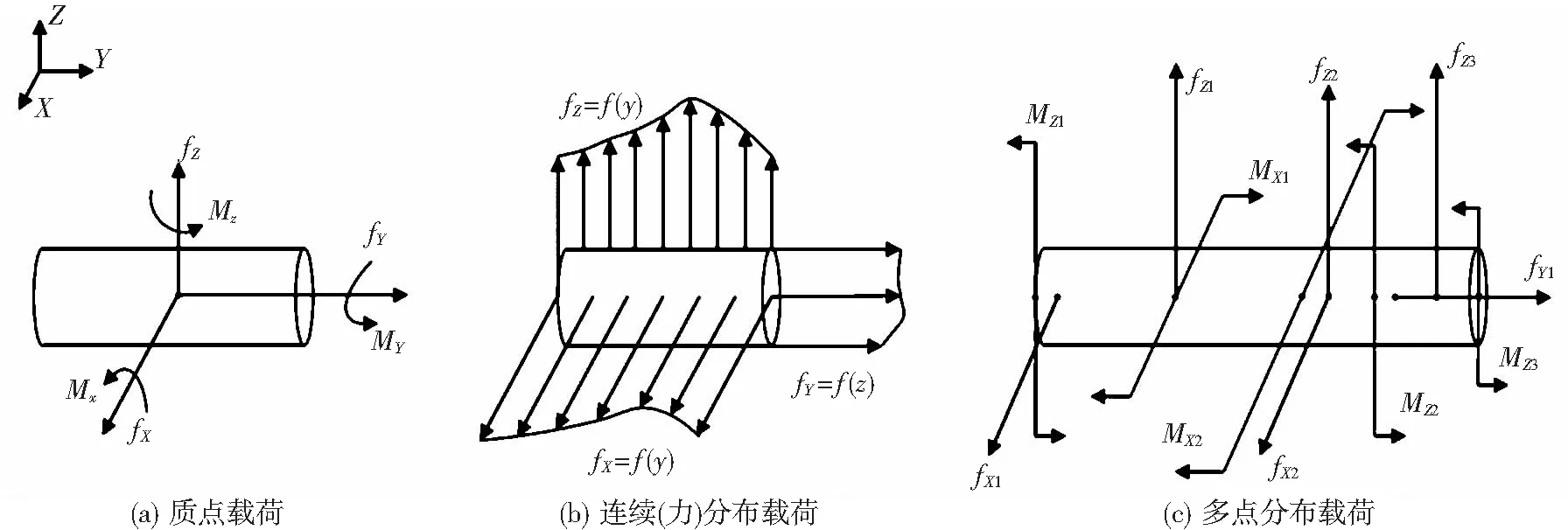
图3 悬吊式试验件载荷分布图

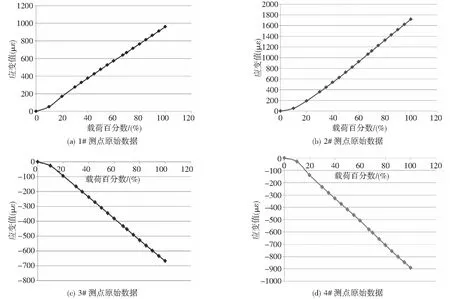
图4 各测点原始应变—载荷级数图

表1 各级载荷下的4个应变测量的实测结果(单位：微应变)

3.2 数据处理

从图4中可以看出，载荷级数在30%之前数据线性较差，且存在突变的拐点，载荷级数30%以后的数据线性较好。分析其原因为直升机机身自重、假件重量以及用于试验的加载及测量设施的重量等因素的影响，使得试验在未开始加载时已有应力，但在试验时，是作为零位处理，因此该应力水平是无法通过测量的方式得到的，在试验全程测量的结果都未包含自身重量造成的影响，因而造成测量数据偏移，不能反映结构在载荷作用下的真实应变值。而且对比理论有限元分析计算数据，发现实测数据普遍存在偏小的情况。针对该情况，对测量数据进行规律寻找和修正处理，还原其结构本身在各级载荷作用下应该有的应力水平。对上图中4个测量点的数据进行分析，得到其规律性，在所有载荷加载点均有载荷时，其测量结果线性规律都很好。因此，采用了从30%到67%进行线性拟合，得到拟合方程：

y=a+bx

分析认为，式中截距a即为自重产生的应变。具体的数据处理过程如下章节。

3.3 线性回归

一组静力试验测量数据(xi、yi；i=1,2,3,…,n)，设yi的测量不确定度相等，且呈线性关系：y=a+bx。

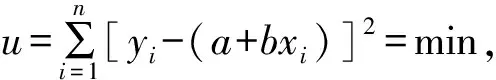
na+(∑xi)b=∑yi

(1)

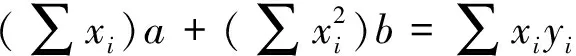
(2)

联立式(1)、式(2)解得：

(3)

(4)

将式(3)、式(4)代入y=a+bx，得线性回归方程。

3.4 零点偏移数据处理

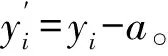
根据上述数据处理方法，先分别将1#至4#测点30%～67%载荷段数据进行线性回归处理，得线性关系：

y1#=9.7244x-12.355;y2#=19.638x-247.54;

y3#=-7.2058x+50.534;y4#=-9.4589x+52.757。

截距分别为：a1#=-12.355；a2#=-247.54；a3#=50.534；a3#=52.757。再进行零点偏移数据处理，得到修正后的线性关系：y1#=9.7244x；y2#=19.638x；y3#=-7.2058x；y4#=-9.4589x。根据修正后的线性关系，用插值法分别得出1#至4#号测点30%载荷之前的数据。修正后应变数据如表2所示。

修正后的的曲线图，如5图所示。

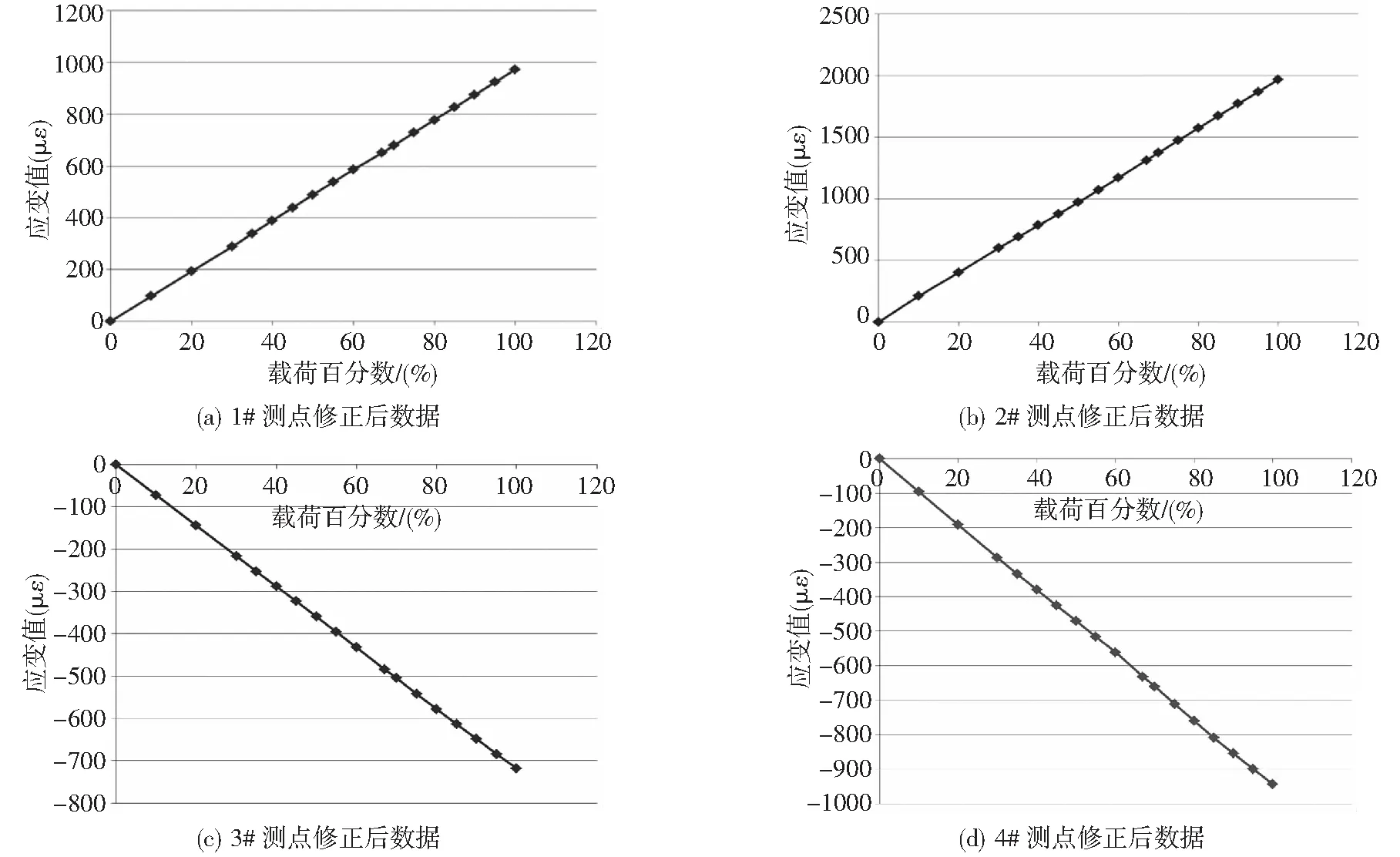
图5 各测点修正后应变—载荷级数图

表2 各级载荷下的4个应变测量的修正后结果(单位：微应变)

对比表1和表2、图4和图5，表明经数据修正处理后，扣除了结构重量等垂向载荷的影响，应变数据线性较好，与理论值较接近，真实地反映了测量点应变与载荷间的变化规律，提高了数据的准确性。

4 结论

通过确定数据区间，根据基于最小二乘法的线性回归进行线性拟合，得出截距并采用零点偏移数据处理方法，最终得到修正后的应变数据。结果表明，该方法修正了悬吊式静力试验中因试验件结构重量、假件重量、加载设备及测试设备重量等因素对试验数据结果造成的影响。同时，该方法快速简易，在实际工程应用中可操作性强，明显提高了应变测量数据的真实性，今后可广泛应用于各类悬吊式静力试验应变测量中。

参考文献：

[1] 顾松年．结构试验基础[M]．西安: 西北工业大学出版社，1996．

[2] 田 垅，刘宗田.最小二乘法分段直线拟合[J]. 计算机科学，2012，39(6A)：482-484.

[3] 贺 谦.全尺寸结构试验应变数据线性化修正方法研究[J].现代计算机，2014(9)：38-40.

[4] 蔡向朝.变载荷外悬挂机构静力试验机的研究[J]. 机械设计与制造,2009(4)：160-162.