共轴刚性旋翼高速直升机配平及旋翼系统气动特性研究

吴裕平，习 娟，范 俊

(1.中国直升机设计研究所，江西 景德镇 333001；2.陆军航空兵研究所，北京 101121)

0 引言

相对于单旋翼带尾桨式常规直升机，共轴刚性旋翼高速直升机采用共轴双旋翼及尾推桨的复合构型，既保持了直升机固有的悬停和低速性能，又充分利用了旋翼前行侧动压大的优势，升力几乎只由前行侧提供，同时采用尾推桨作为辅助推进装置，从而实现高速飞行。美国西科斯基飞机公司研制的X2技术验证机是该构型高速直升机的典型代表，2010年,X2飞行速度达到463km/h。

共轴刚性旋翼高速直升机的气动面多，操纵复杂，在垂直起降、悬停和低速飞行状态下，通过操纵旋翼总距、纵横向周期变距和差动角以直升机模式飞行。在中高速飞行状态下，升力由旋翼产生，通过操纵尾部推进桨桨距、升降舵、方向舵，并结合旋翼操纵，来保持平衡，实现稳态飞行[1]。

高速直升机由于要考虑高速飞行，所以需要采用不同于常规直升机的桨叶气动外形设计，旋翼气动特性呈现出较大的差异。在90°方位角处且靠近桨尖的位置会出现较强的激波；在270°方位角处且靠近桨根的位置会出现较强的反流，且会产生负升力。文献[2]对高速旋翼流动机理、桨叶压力和流场细节开展了研究。

随着美国S97技术验证机的研制，国内外掀起了高速直升机技术研究的高潮。基于CFD方法，国内研究了共轴刚性旋翼的气动干扰特性[3]，分析了高速直升机机身、双桨毂的流场特性[4]，并针对高速直升机的反流区较大的特点，开展了其对旋翼气动特性的影响研究[5]。本文基于旋翼叶素理论和涡流理论，建立全机平衡方程，根据全机配平情况，研究共轴双旋翼、尾部推进桨的气动特性。

1 全机配平模型

共轴刚性旋翼高速直升机的气动力部件包括上/下旋翼、尾推桨、机身(无机翼，含平尾、垂尾)，平尾上安装升降舵，垂尾上安装方向舵。

1.1 旋翼气动力模型

考虑桨盘平面内诱导速度的非均匀分布，近似认为诱导速度沿展向和周向线性变化，表达式为：

λ(r,Ψ)=λ0(1+Kxx+Kyy)=

λ0(1+KxrcosΨ+KyrsinΨ)

(1)

其中，λ0为诱导速度的平均值，Kx、Ky是前飞状态诱导速度变化参数，经典涡流理论给出许多Kx和Ky参数的估算方法，由Drees给出的参数估计为：

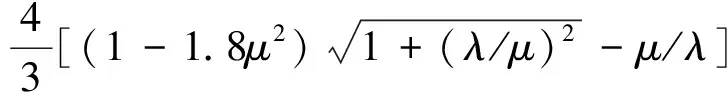
(2)

Ky=-2μ

(3)

式中，χ是桨盘处的尾迹倾斜角。考虑共轴双旋翼之间的相互干扰，引入干扰因子，于是下/上旋翼的平均诱导速度修正为：

λ01=ν1+δ1ν2

(4)

λ02=ν2+δ2ν1

(5)

式中，ν1、ν2分别为下、上旋翼桨盘处本身固有的平均诱导速度，由滑流理论得到。

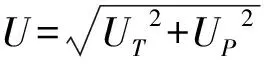
(6)

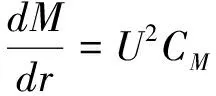
(7)

式中，M=UΩR/Cs，Cs是当地声速，Cl与Cd、CM为剖面翼型的升力系数、阻力系数、力矩系数，是与迎角和马赫数有关的函数，来源于风洞试验数据。

最后，通过积分计算得到旋翼的气动力和力矩。

尾部推进桨的气动模型与旋翼类似，只不过它只有总距操纵，没有纵横向周期变距。将尾推桨桨叶进行离散分段，根据叶素理论得到各个分段的升力、阻力和力矩，然后将处于不同方位角的各片桨叶的载荷进行积分，就得到整个尾推桨的载荷。

1.2 机身气动力模型

这里定义的机身为除去共轴双旋翼和尾推桨的直升机部分，其气动力根据CFD计算或风洞试验得到。机身空气动力系数包括：阻力系数CDF、升力系数CLF、侧力系数CSF、滚转力矩系数CMXF、偏航力矩系数CMYF、俯仰力矩系数CMZF，它们都是直升机迎角α、侧滑角βS、升降舵偏角δe、方向舵偏角δr的函数。

由这些空气动力系数和机身模型的特征长度IF、特征面积AF及远方来流动压q，得到直升机机身的空气动力为：

(8)

1.3 全机配平模型

直升机稳定飞行时，三个方向的力和力矩均趋于零。综合下旋翼、上旋翼、尾推桨、机身的气动力与重力，可以得到全机六力素，则前飞状态下直升机的平衡方程为：

∑FX=0：FX，1+FX，2+FX，3+FX，F-Gsinϑ=0

∑Fy=0：Fy，1+Fy，2+Fy，3+Fy，F-Gcosϑsinγ=0

∑FZ=0：FZ，1+FZ，2+FZ，3+FZ，F-Gcosϑcosγ=0

∑MX=0：MX，1′+MX，2′+MX，3′+MX，F′=0

∑My=0：My，1′+My，2′+My，3′+My，F′=0

∑Mz=0：Mz，1′+Mz，2′+Mz，3′+Mz，F′=0

平衡方程是非线性方程组，需要使用数值方法进行求解，得到姿态角ϑ、γ和操纵量φ7、A1、B1、φT、δe、δr。有别于常规构型直升机，高速直升机多了两个操纵量，方程组的解不唯一。此时可以假设姿态角为某一特定值，再去求方程组的解。使用Newton法求解上述非线性方程组可以得到比较满意的结果。

1.4 平飞状态简单配平模型

在常用的平飞状态下，可以把三维平衡问题简化为二维平衡问题。纵剖面内(即XZ剖面，俯仰方向)的作用力，包括重力，上、下旋翼的拉力、力矩，尾推桨的推力，以及机身产生的气动阻力和力矩。详见图1、图2所示。

图1 全机作用力示意图

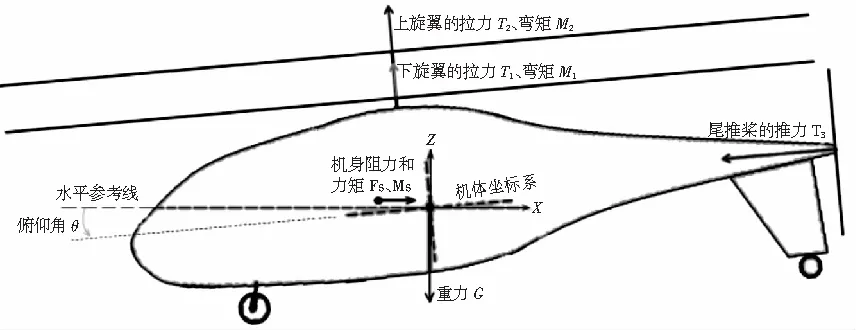
图2 纵剖面作用力示意图

平衡方程式：

(10)

T1×cosθ+T2×cosθ+T3×sinθ=G-

T1×sinθ-T2×sinθ+T3×cosθ=FS-

T1×X1-T2×X2+T3×Z3+M1+M2=

MS+FS×ZS×cosθ

(11)

式中，θ为机身俯仰角，抬头为正；X1、X2为下、上旋翼到重心的纵向距离；Z3、Zs为尾推桨、机身气动作用点到重心的垂向距离；机身气动阻力Fs、力矩Ms在机身外形方案确定后，取决于机身俯仰角和升降舵偏角。

一般情况下，θ小，则sinθ=θ(θ单位弧度)，cosθ=1；同时，X1=X2，T1=T2，M1=M2，于是方程式进一步简化为：

2×T1+T3×θ=G-2×T1×θ+T3=F3-

2×T1×X1+T3×Z3+2×M1=MS+FS×ZS

(12)

悬停状态下，由于Fs=0，Ms=0，尾推桨空转，推力接近0，上、下旋翼拉力假设相等，那么方程式的典型解为：

(13)

结果说明，上、下旋翼产生的拉力之和等于重力，同时需要通过纵向周期操纵使旋翼产生力矩，用于平衡其拉力相对重心产生的力矩。

对于平飞状态，可以操纵平尾上的升降舵转角，调整机身气动力矩MS=f(v,θ,δe)，同时也可以操纵旋翼纵向周期变距进行配合，实现力矩达到平衡状态。

通常，为了提高飞行性能，希望大部分飞行状态下的气动效率高，机身气动阻力小，使得机身俯仰角接近0，于是可以得到一组解：

θ=0

T1=T2=G/2

T3=FS

MS=2×M1-G×X1+FS×(Z3-ZS)

(14)

2 共轴旋翼的气动特性分析

直升机受旋翼工作原理限制，前行侧桨叶激波、后行侧桨叶动态失速容易导致阻力、铰链力矩和交变载荷激增[7]，随着飞行速度的提升，旋翼的反流区域逐渐增大[8]。因此，旋翼桨尖的合速度通常不超过0.9Ma。常规构型直升机，最大飞行速度300km/h时，旋翼旋转的桨尖速度一般不超过220m/s；高速直升机，最大飞行速度450km/h时，旋翼旋转的桨尖速度一般不超过180m/s。所以，相对于悬停/低速飞行状态，高速飞行时降低旋翼转速，可以减少旋翼需用功率，从而提高飞行性能[9]。

为了解决转速变化带来的动力学问题，高速直升机采用共轴刚性旋翼。刚性旋翼取消了挥舞、摆振铰，再加上大前进比，旋翼气动环境与常规直升机相差甚大。共轴刚性旋翼大反流、强径向流、变转速运行环境，带来旋翼气动性能、载荷的一系列变化。

2.1 悬停状态

在悬停状态下，随着总距的增加，旋翼拉力和功率增大。随着转速的降低，相同总距下的旋翼拉力和功率减小。为了保持旋翼拉力不变，需要增加总距，旋翼转速降至90%总距增加约1.3°，旋翼转速降至80%总距增加约3.1°。图3给出了旋翼悬停效率的变化情况，可以看出：随着拉力系数/实度的增加，悬停效率先增大后减小，最大悬停效率约0.76；转速降低，最大悬停效率增加；在相同拉力下，随着转速的降低，悬停效率略有提高。

图3 旋翼悬停效率

由于没有挥舞铰，旋翼周期操纵不能引起桨盘倾斜，但由于升力偏置，会产生附加弯矩。基于此，高速直升机可以在悬停或低速飞行状态下，通过周期变距操纵配平直升机或者改变飞行状态。从图4中可以看出：随着纵向周期变距的增加，桨毂弯矩线性增大；旋翼转速对桨毂弯矩的影响明显，在旋翼拉力相同的状态下，即使纵向变距相同，桨毂弯矩也会随着转速的降低而减少。

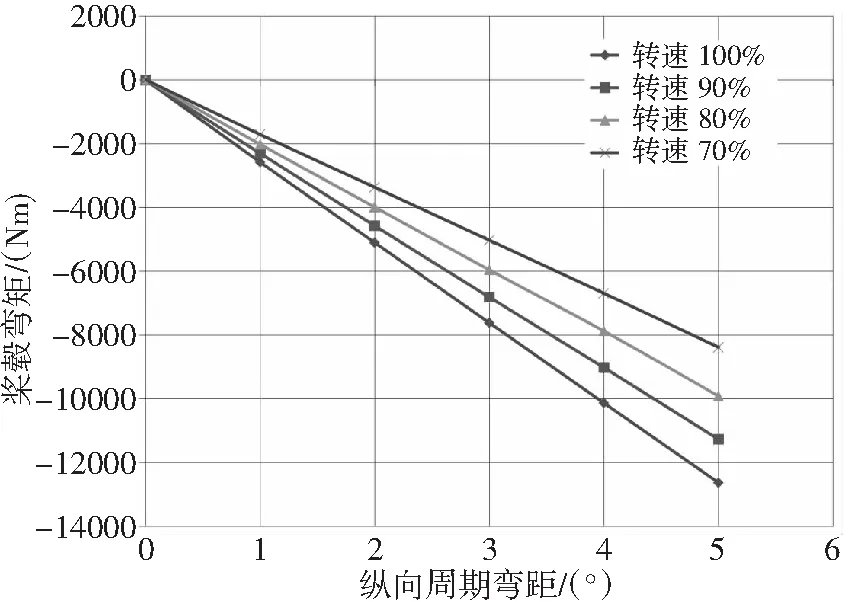
图4 旋翼桨毂弯矩(悬停纵向操纵)

2.2 平飞状态

前飞时旋翼的气动效率较高，前飞升阻比随着飞行速度先增大后减小，最大升阻比可达10(见图5)。飞行速度增加时需要降低旋翼总距(见图6)，以保持旋翼拉力不变。相同飞行状态下，随着旋翼转速的降低，需要的总距增加，产生的桨毂弯矩也增大(见图7)。随着旋翼转速的降低，相同拉力下的需用功率降低。特别是转速较低时，大速度飞行时的旋翼功率为负，即处于风车状态，如图8所示。

图5 旋翼前飞升阻力

从旋翼的有效攻角和诱导速度来看，如图9、图10所示，直升机高速飞行时，旋翼处于风车状态下，桨叶剖面的有效攻角变化范围较大，在270°方位桨根附近出现大范围的反流区，即气流从桨叶后缘流向前缘；诱导速度整体数值较小，而且90°至180°方位的桨尖区域出现从桨盘下方流向上方的气流。

图7 前飞时旋翼桨毂弯矩

图8 前飞时旋翼功率

3 尾推桨的气动特性分析

高速直升机尾部推进桨主要提供前进力。在悬停和小速度飞行时，尾推桨空转不提供推进力；大速度飞行时，操纵尾推桨总距，产生所需推进力以抵消阻力，从而实现高速飞行。由于尾推桨的气流环境不同于旋翼，桨盘竖直，与来流接近垂直，近似于轴流状态，导致其总距操纵特别大(见图11)，通常采用大扭转率叶片设计。

图9 前飞旋翼桨叶剖面的有效攻角

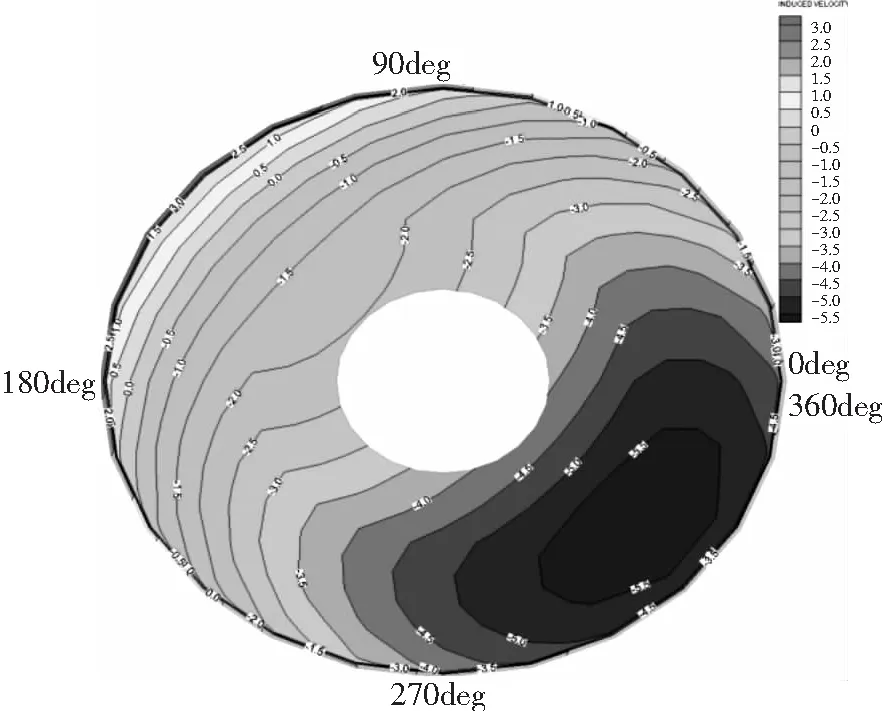
图10 前飞旋翼桨盘诱导速度分布

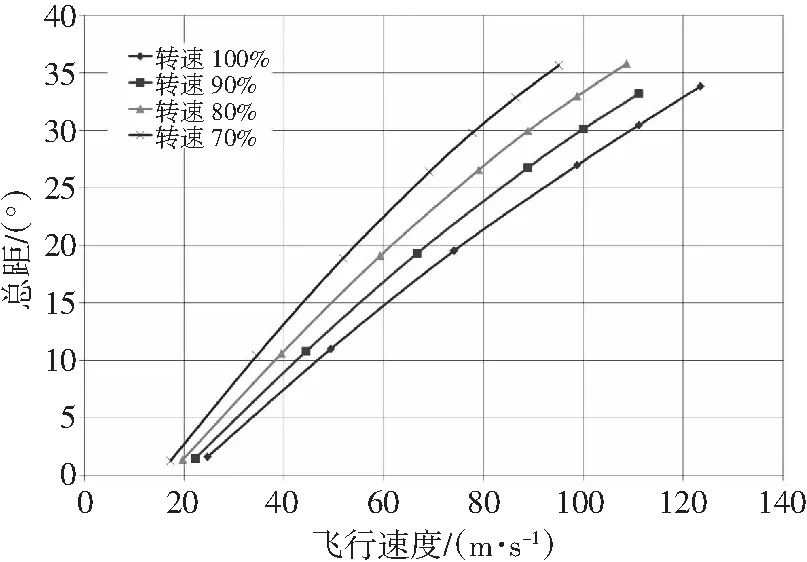
图11 尾推桨总距随飞行速度的变化

随着飞行速度的增加，机身阻力面积一定时，尾推桨推进力和功率需求急剧增大；转速降低后，为了保持相同推力，需要增加总距，但功率需求基本不变，如图12所示。如果阻力面积增加，一定飞行速度下，尾推桨的推力和功率基本上同比例增加(见图13)。

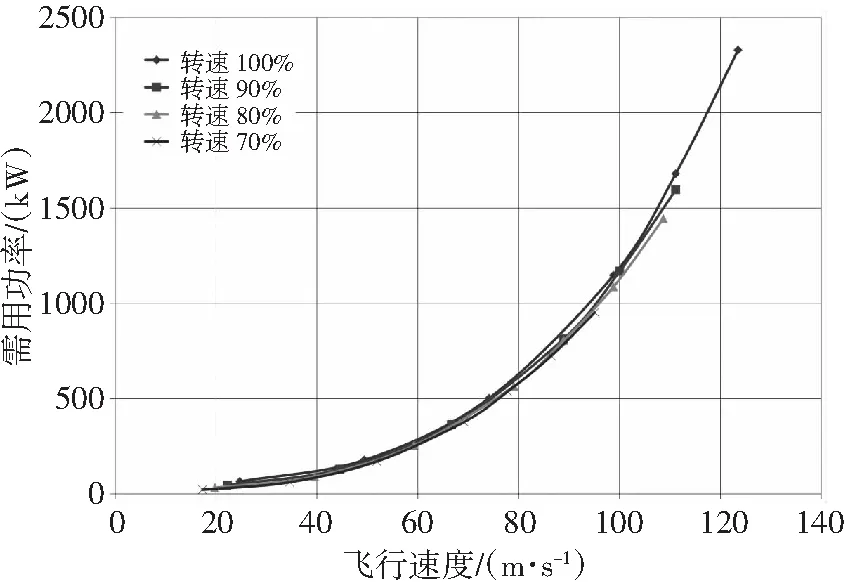
图12 尾推桨需用功率

图13 全机阻力面积对尾推桨功率的影响

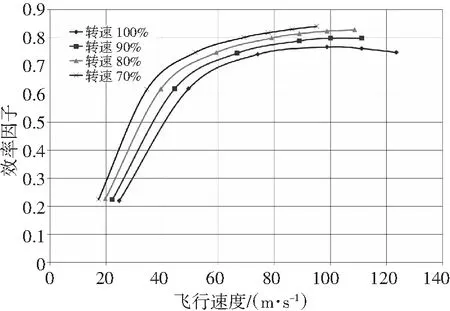
图14 尾推桨的气动效率

4 全机功率特性分析

高速直升机全机功率主要包括共轴双旋翼和尾推桨的需用功率(不考虑传动损失和附件消耗等)，它随着飞行速度先减少后增大。共轴双旋翼的功率随着飞行速度逐渐降低，而尾推桨的功率随着飞行速度逐渐增大，特别是大速度时其增加幅度更猛。

共轴双旋翼和尾推桨的需用功率在全机功率中所占的比重如图15所示：悬停和小速度平飞时，尾推桨比重很小；大速度平飞时情况相反，共轴双旋翼比重很小，尾推桨功率比重最大接近90%。大概在飞行速度230km/h时，两者需用功率相当。

图15 双旋翼和尾推桨的功率占比

图16给出了不同转速下各部分功率的变化情况，当旋翼转速降低(推进桨转速同步降低)时，全机总功率随之降低。其中，共轴双旋翼的需用功率减少，推进桨的功率反而增加。实际上，由于高速直升机的平衡状态不是唯一的，各部分功率的变化跟操纵和配平姿态存在一定的联系，机身俯仰角和旋翼纵向操纵均在一定程度上影响着推进桨的推力及其功率值。

图16 不同转速下各部分功率情况

高速前飞时，以升降舵、方向舵操纵为主控制机身姿态，但旋翼产生的俯仰力矩(使机身抬头)不小，只靠平尾作用力难以平衡(除非平尾面积和舵面偏转角足够大)，而配合旋翼的纵向操纵，可以取得较好效果。同时，尾推桨将产生滚转力矩，需通过旋翼横向操纵予以平衡。因此，只有在共轴双旋翼、尾推桨、尾部舵面的共同操纵控制下，才能达到全机平衡和机身姿态较小的最佳状态。

图17给出了高速直升机的主要操纵量随飞行速度的变化情况，旋翼总距先减小后增大，升降舵偏角随飞行速度不断降低，尾推桨总距不断增加，低转速时的操纵量均大于高转速时。

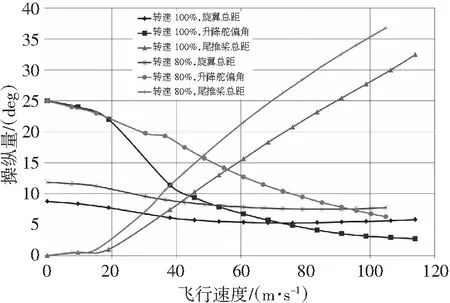
图17 全机配平的主要操纵量

5 结论

本文针对共轴刚性旋翼+尾部推进桨的复合构型高速直升机，建立了简单实用的全机配平模型和部件气动力模型，重点分析了旋翼、尾推桨的转速、总距、拉力、功率、载荷之间的关系，得到了不同飞行状态下的操纵量和功率水平。通过配平模型应用和算例分析，探讨了高速直升机气动特性的一般规律：

1)共轴刚性旋翼的桨毂载荷偏大，气动效率高，转速降低，最大悬停效率增加，高速飞行时的气动环境存在一系列异常现象。

2)尾推桨的需用功率取决于全机阻力，而与转速关系不大。

3)低速、高速飞行时，全机功率分配比例差距很大，悬停和低速状态以共轴刚性旋翼为主，高速状态以尾部推进桨为主。

4)多裕度操纵通道导致配平结果的非唯一性，通常选取机身姿态小和全机功率低的典型解。

本文的计算方法和研究结论，仅限于稳定飞行状态，并有待于飞行试验验证，但以此作为新概念高速直升机相关研究的起点，为下一步研究奠定了基础。机动飞行状态将更加复杂，飞行力学和气动特性急需深入研究，以推动高速直升机的技术进步和装备发展。

参考文献：

[1] 段赛玉,陈铭.复合式共轴直升机飞行动力学数学模型研究.飞机设[J]. 2011,31(03): 0013-0017.

[2] 张 昆,史勇杰,徐国华,等.高速直升机旋翼气动特性分析[C].第二十八届全国直升机年会论文集,2012.

[3] 黄水林,林永峰,等.共轴刚性旋翼气动干扰特性初步分析[C].第二十七届全国直升机年会论文集,2011.

[4] 李文浩,史勇杰,徐国华,等.基于CFD方法的复合式高速直升机气动特性研究[C].第二十八届全国直升机年会论文集,2012.

[5] 孔卫红,陈仁良.反流区对复合高速直升机旋翼气动特性的影响[J].航空学报,2011,32(2):223-230.

[6] Yeo H, Johnson W. Aeromechanics analysis of a compound helicopter[C].62nd Annual Forum of the AHS,2006．

[7] Leishman J G. Principles of Helicopter Aerodynamics,Second Edition[M].Cambridge: Cambridge University Press, 2006.

[8] 袁明川,杨永飞,林永峰.高速直升机旋翼反流区桨叶剖面翼型气动特性CFD 分析[J].直升机技术, 2015(01):01-05.

[9] Nagaraj V T, Chopra I. Dynamics Considerations for High Speed Flight of Compound Helicopters[C]. American Helicopter Society 58th Annual Forum, Montreal, Canada, 2002.

[10] 周国仪，胡继忠，等．共轴式直升机双旋翼载荷计算模型研究[J]．航空动力学报，2003，18(3)：343-347．

[11] Soito S, Azuma A. A Numerical Approach to Co-Axial Rotor Aerodynamics[J]. Vertica，1982,6(3)：253-266.