连续型线性定常系统的能控性与能观测性研究

王新奇

(西安文理学院 科研处(学报编辑部)， 西安 710065)

能控性和能观测性的概念是20世纪60年代Kalman首次提出的，在多变量控制系统中，能控性和能观测性是两个反映控制系统构造的基本特征，是现代控制理论中最重要的基本概念[1-2].目前,现代控制理论中这两个重要问题已经成为了最优控制、最优估计的设计基础.

1 连续型线性定常系统

定义1[3]线性方程组

称为定常线性系统的状态空间表达式，微分方程(1a)称为状态方程，变换方程(1b)成为输出方程.其中：

A∈Cn×n称为系数矩阵，表示系统内部各个状态变量之间的关联情况；

B∈Cn×m称为输入矩阵，表示输入对每个状态变量的作用情况；

C∈Cp×n称为输出矩阵或量测矩阵，表示输出与每个状态变量的组成关系；

D∈Cp×m称为直接传递矩阵；

x∈Cn×1称为状态向量；

u∈Cm×1称为输入或控制向量；

y∈Cp×1称为输出向量.

当D=O时，表明不考虑输入对输出的直接传递，系统可简记为(A,B,C)，称为多输入多输出系统.若状态向量x及输入向量u退化为一元变量时，成为单输入单输出系统.

2 状态转移矩阵

定义2 矩阵指数函数：Φ(t)=eAt称为状态转移矩阵.

矩阵指数函数eAt是一个关于时间t的函数矩阵，它能不断地把初始状态变换为一系列的状态向量，它起着一种状态转移的作用.

状态转移矩阵eAt具有如下几个性质[4]：

(1)Φ(t)Φ(τ)=Φ(t+τ);

(2)Φ(t-t)=Φ(0)=I；

(3)Φ(t)总是可逆的，并且Φ-1(t)=Φ(-t)；

3 连续型线性定常系统的能控性和完全能控性

定义3[4]对于一个线性定常系统，若在某个有限时间区间[0,t1]内存在着输入u(t)(0≤t≤t1)，能使系统从任意初始状态x(0)=x0转移到x(t1)=θ，则称该状态x0是能控的；若系统的所有状态都是能控的，则称该系统是完全能控的.

定理1[5]连续型线性定常系统(A,B,C)完全能控的充分必要条件是矩阵

为非奇异矩阵.

证首先证明充分性.

设Wc(0,t1)非奇异，对方程(1a)从0到t1积分可得

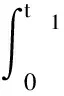
(2)

令

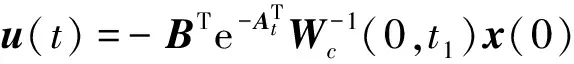
(3)

将u(t)代入式(2)可得

这说明在式(3)所示的控制输入u(t)的作用下，能使系统从x(0)转移到x(t1)=0.

再证必要性.用反证法.若系统是完全能控的，但是Wc(0,t1)是奇异的，则引出矛盾.

因为Wc(0,t1)是奇异的，则必定有非零向量α=(a1,a2,…,an)T使对任意时刻t=t1≥0,有下式能够成立.

αTWc(0,t1)α=0

即

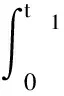
所以，对于任意时刻t，都有

αTe-AtB=0,t≥0

又系统是完全能控的，由充分性，必存在某个u(t),使其作用于系统上，使x(t1)=0,因此由式(2)可得

上式两边同时乘以αT,便有

由x(0)的任意性，现选初始状态x(0)=α,则有αTα=0.这与α为非零向量相矛盾.所以Wc(0,t1)是非奇异的.定理得证.

定理1从理论上给出了连续型线性定常系统是否完全能控的判别准则，但是在实际应用中还比较复杂.本文给出一个较为简便实用的判别准则.

定理2 连续型线性定常系统(A,B,C)完全能控的充分必要条件是n×mn矩阵

Wc=(B,AB,A2B,…,An-1B)

的秩为n(即Wc为行满秩矩阵).Wc称为能控性矩阵.

证充分性.用反证法.如果系统(A,B,C)不是完全能控的，则由定理1可知，Wc(0,t1)是奇异的，因此存在非零向量α，使得

αTe-AtB=0.

两边同求k次微商可得

αT(-A)ke-AtB=0,k=1,2,…,n-1

令t=0，可得

αTAkB=0,k=1,2,…,n-1

而当t=0时，由αTe-AtB=0得

αTB=0

所以，对于k=1,2,…,n-1,都有αTAkB=0，即

αT(B,AB,A2B,…,An-1B)=0(α为非零向量)

这与矩阵Wc的秩为n相矛盾.因此，系统是完全能控的.

例1 设

判断系统(A,B,C)是否完全能控.

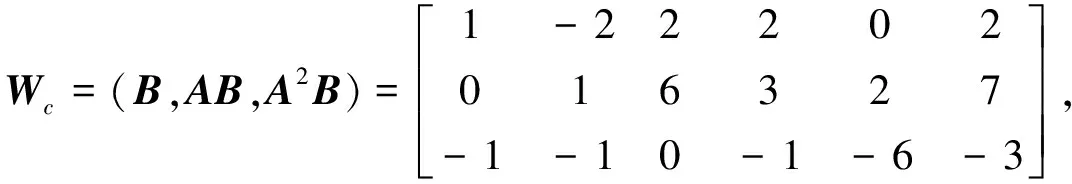
4 连续型线性定常系统的能观测性

定义4[4]对于一个线性定常系统，若在有限的时间区间[0,t1]内，能通过观测系统的输出y(t)而唯一地确定任意初始状态x(0)，则称该系统是完全能观测的，或称对于每个状态x(0)是能观测的.

定理3[5]连续型线性定常系统(A,B,C)完全能观测的充分必要条件是n阶对称阵

是非奇异矩阵.

证充分性.

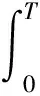
令

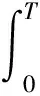
可得

CeAtx(0)=η(t)

(4)

以eATtCT左乘上式两边，并从0到t1进行积分，可得

即

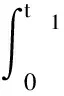
由于M(0,t1)为非奇异矩阵，则

因此，x(0)是可以唯一确定的.所以系统是完全能观测的.

再证必要性.用反证法.设系统是完全能观测的，如果M(0,t1)是奇异的，则存在非零n维向量α，使得对于任意的t≥0,都有

αTM(0,t1)α=0

即

这表明了对任意的t≥0,都有

CeAtα=0

取α=x(0)≠0,则CeAtx(0)=0.这与当x(0)=0时，由式(4)

η(t)=CeAtx(0)=0

的结果相比较，说明x(0)不能唯一确定.这与系统是完全能观测相矛盾.因此，M(0,t1)为非奇异矩阵.

定理4 连续型线性定常系统(A,B,C)完全能观测的充分必要条件是pn×n矩阵

的秩等于n(即W0为列满秩矩阵).矩阵W0称为能观测矩阵.

例2 判定线性系统

的能观测性.

解能观测性矩阵为

W0的秩为2，所以系统是能观测的.

由此可见,定理2和定理4可以很方便的判断线性系统的完全能控性和能观测性.

[参 考 文 献]

[1] 王永茂.矩阵分析[M].北京：机械工业出版社，2010.

[2] 同济大学数学系.线性代数[M].北京：清华大学出版社，2007.

[3] 罗家洪，方卫东.矩阵分析引论[M].4版.广州：华南理工大学出版社，2006.

[4] 钟裕林，王新奇，陆军.线性代数与矩阵分析方法[M].长春：吉林大学出版社，2011.

[5] 谢广明，郑大钟.一类混合动态系统的能控性和能观性研究[J].控制理论与应用，2002(1)：139-142.