基于MATLAB的小波分析在信号去噪中的应用

曹银萍，郭 璐

（西安石油大学机械工程学院 陕西 西安 710065）

1 引言

目前，采集信号时没有办法完全避开其他干扰信号的影响，最终采集的信号总是夹杂着噪声，这种现象往往导致采集的信号失真，所以对信号进行消噪是信号处理中的一个重要问题。传统的去噪方法有很多，其中，Fourier变换建立了时间域和频率域相互转换的关系，但Fourier变换以正弦波及其高次谐波为标准基，不能分析局部频率。加窗Fourier变换一定程度上克服了Fourier变换的局限性，但其本身是单一分辨率的分析方法[1]。为了寻找更加合适的方法进行信号去噪，20世纪80年代兴起了一种新的时频交互分析方法即小波分析[2]。与Fourier变换相比，小波分析是时间频率的局部化分析，通过伸缩平移运算对信号逐步进行多尺度细化分析，最终达到在低频部分具有较高的频率分辨率和较低的时间分辨率，在高频部分具有较高的时间分辨率和较低的频率分辨率。小波分析解决了Fourier变换不能解决的许多难题，是调和分析发展史上里程碑式的进展，因此小波分析被称为“数学显微镜”[3]。

2 小波分析的概述

小波即小的波形，是指具有衰减性的波形。1974年，从事石油信号处理的法国地质专家J.Morlet第一次提出了小波变换的概念并建立了反演公式，但没有得到当时数学家的认可[4]。J.O.Stromberg构造了和现在使用的小波基相似的小波基[5]。1986年，科学家Y.Meyer首次构造出真正的小波基[6]，并与S.Mallat联合建立了构造正交小波基的统一方法及多尺度分析。之后的比利时女数学家I.Daubechies的学术著作《小波十讲》（Ten lectures on Wavelets）对小波的普及具有重要的推动作用[7]。

2.1 简述Fourier变换

对于f(t)∈L空间的能量信号，即时间连续信号f(t)的傅里叶变换定义为

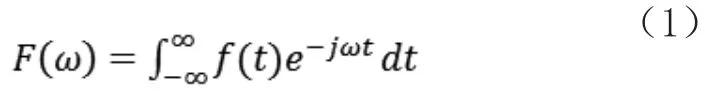
傅里叶变换完成了时域函数和频域函数的变换，但在转化中丢失了时间信号，几乎没有分辨率。因为傅里叶变换和逆变换是独立的，所以只能单独分析时域特性和频域特性，不能将其放在一起研究[8]。

2.2 简述短时Fourier变换

为了克服Fourier变换不能描述局部时频特性的局限性，1946年Gabor提出了短时Fourier变换，它就是时间信号加窗后的傅里叶变换，定义为

此时，ωbF(ω)给出了时间信号在时间窗[t*+b-∆ω，t*+b+∆ω]的局部信息。因为加窗的Fourier变换后形状、大小均与时间、频率无关，这个窗口一旦确定后，其大小和形状均不变。信号处理时高频信号需要用较短的时间窗分析，而低频信号需要用较宽的时间窗分析，生活中的绝大部分信号都属于非平稳信号，因此，短时Fourier变换在信号分析的应用仍有很大的局限性。

2.3 简述小波分析

如果把ψa，b(t)代替短时傅里叶变换中的窗口函数ωω，b(t)，其中

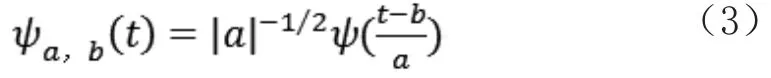
那么式（2）变为

式（4）为小波变换的定义式。

小波变换很好的解决了傅里叶变换和短时傅里叶变换的不足，既可分析信号的局部特征，其窗口大小又可变。小波变换具有低熵性，多分辨率，可去除信号的相关性，可根据信号特点灵活选择基函数等特性，适合用来处理非稳定信号，在噪声消除，特征信号的提取，图像处理等方面的应用获得显著成果。

3 小波分析信号去噪的原理

被噪声污染的信号f(n)模型一般表示为

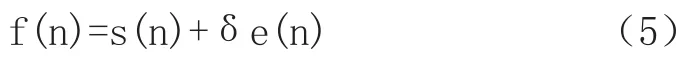
其中，s(n)是原信号，e(n)是噪声，δ是噪声强度[4]。

小波去噪是为了消除e(n)，还原s(n)。小波去噪的过程一般分为3个步骤：

（1）信号分解。信号采样后，对信号进行小波分解，根据信号特性选定小波基并确定分解层数，进行分解计算。

（2）信号处理。对小波分解后的高频系数选择合理阈值进行软阈值量化处理，把不需要的频率舍弃。

（3）信号重构。根据小波分解的最底层低频系数和每层高频系数进行一维小波重构。

其中最关键的是信号处理这一步骤，阈值的选择和阈值量化处理关系着信号的消噪质量。研究信号去噪方法的进程中主要出现了三种方法：小波分解与重构算法，误差很大；交替投影法，计算量大；小波阈值收缩去噪法，误差小，方便计算，目前仍大量使用。文章依托小波阈值去噪法，分析小波分析在信号去噪中的应用。

4 三种方法用MATLAB实现信号去噪的仿真对比

以含噪的doppler信号为例，采集信号后分解，以不同的方式对信号进行去噪处理，最终重构信号，达到不同效果的信号去噪结果。文章统一选用dbN小波基进行MATLAB仿真。

4.1 通过抑制细节系数去噪

在MATLAB中采集noisdopp信号后，用db6小波基对信号进行5层分解，再对细节系数进行缩放为原来的四分之一进行抑制，抑制后重新构建信号。

图1 抑制细节系数去噪前后信号对比图

从图1可知抑制细节系数基本可以达到去噪的效果，但只是考虑细节系数并没有把噪声的性质考虑进来，去噪效果比较差，原始信号丢失的比较严重。

4.2 通过FFT（快速傅里叶变换）实现信号去噪

在MATLAB中实现快速傅里叶变换消噪的步骤和小波分析消噪的步骤大致相同，不同的是在进行信号处理时FFT是分析频谱，抑制不需要的频谱。

图2 FFT去噪前后信号对比图

由MATLAB仿真结果图2可知，滤波后的信号把最初的原信号都丢掉了，所以傅里叶变换时会把它自身无法分析的区域直接舍弃，严重时会导致信号失真。

4.3 通过小波阈值收缩去噪法去噪

小波阈值收缩去噪法即MATLAB默认的去噪法，是根据方差最小原则，对系数偏似然估计确定阈值。仿真时使用dbN小波基对信号进行分解，阈值处理时选用全局阈值处理和分层阈值处理两种方法，并使用软阈值方法对信号去噪。

图3 小波阈值去噪前后信号对比图

由仿真结果图3可知，分层阈值去噪后的信号比全局阈值去噪后的平滑，但丢失了一部分原信号。使用阈值去噪后的信号保留了原信号绝大多数特性，尤其保留了初期信号的高频特性。信号去噪的两个基本要素是光滑性和相似性，相比前两种方法，小波分析更能满足这两个要素。

5 结语

文章在概述小波分析的研究进展，小波分析理论和小波分析消噪原理的基础上，利用MATLAB仿真信号去噪前后信号能量对比图，分析不同方法下的信号消噪效果。得出与抑制细节系数消噪和FFT消噪法都有自身不可消除的缺点相比，小波分析的阈值消噪法能够在防止信号失真的前提下最大程度消除信号中噪声的结论。

[1] 王芳.小波分析在信号去噪中的应用研究[D].西华大学，2009.

[2]刘志松.基于小波分析的信号去噪方法[J].浙江海洋学院学报，2011，30(2):150-154.

[3] 张仁辉，杜民.小波分析在信号去噪中的应用[J].计算机仿真，2005，22(8)：69-72.

[4] 蔡静.MATLAB R2015a 小波分析[M].清华大学出版社，2016.

[5] 彭圆圆.小波分析在一维信号去噪中的应用[D].北京邮电大学，2011.

[6] Y.Meyer，“Principe d’incertitude，bases hilbertiennes et algebres d’operateurs，” Seminaire N.Bourbaki，1985-1986，Nr.662.

[7] I.Daubechies，Ten lectures on Wavelets.Philadelphia:PA:SIAM，1992.

[8] 刘君华，等.智能传感器系统[M].西安电子科技大学出版社，2010.