多目标约束下半导体制冷片几何结构参数的优化设计

(浙江大学制冷与低温研究所 浙江省制冷与低温技术重点实验室 310027)

热电制冷又称为半导体制冷，制冷片(图1)是由N对pn结通过串联的方式连接在一起，p结和n结分别由两种具有不同塞贝克系数的材料组成。当有电流通过时，由于帕尔贴效应的存在，两种材料的接头一端放热，一端吸热[1]，实现制冷的目的。半导体制冷与一般制冷的显著区别在于：不使用制冷剂，没有运动部件，容量尺寸宜于小型化，使用直流电工作[2-3]，制冷量可从mW级到kW级变化，制冷温差可达20～150 ℃[4]。因此，半导体制冷在实际生产生活中有着广阔的应用前景，被广泛应用于电子制冷[5-6]、便携式冰箱[7-9]等领域。

图1 半导体制冷片Fig.1 Thermoelectric cooler

针对半导体制冷片的制冷量和制冷效率(COP)优化已有大量的研究，优化方法可分为以下3方面：

1)改变半导体制冷片自身的几何参数(如pn结长度[10-14]、pn结对数[9,12])对制冷效果进行优化；

2)改变制冷片冷热端的传热方式[15-16]，或改变制冷片冷热端的传热热阻[17-19](包括制冷片冷热端的传热面积及传热系数)对制冷片制冷系统进行热设计和优化；

3) 对制冷片的输入电流[2,20]进行优化设置。

但被冷却设备(如：激光二极管、红外传感器)体积的小型化使其所需的散热热流密度增大，同时制冷片的散热空间和散热方式受到限制，使改变制冷片自身的几何参数成为优化制冷量和COP的有效方法。当确定制冷片的材料特性和冷热端温度时，Cheng Y. H.等[10]利用遗传算法研究在一定输入电流情况下pn结截面积、高度及pn结数目对制冷量和COP的影响。G. Fraisse等[11]研究了当冷端和热端温度一定，n结体积和长度不变时，n结截面积改变对制冷量和COP产生的影响。G. Min等[12]研究了在一定制冷片冷热端温度情况下，pn结的长度对制冷片的制冷量和COP的影响。当固定电流及固定制冷片冷热端温差(冷端温度保持300 K)时，利用共轭梯度法，Huang Yuxian等[13]研究了pn结数目、pn结长度和截面积对制冷量的影响，从而优化制冷量。Zhu Wei等[14]研究了当恒定电流和温差(热端温度保持27 ℃)，pn结长度与横截面积比相同时，不同尺寸(pn结长度或者横截面)对制冷片制冷量的影响。

以上文献均是基于给定的制冷片冷热端温度，研究制冷片几何参数对制冷量和COP的影响。1)制冷片的冷热端温度预先给定。为了维持恒定的冷热端温度，意味着制冷片外部的冷热端热阻(或热源、热汇的温度)可随工况改变任意调整，这在实际应用中难以实现。2)均是以制冷量和COP为优化目标，忽略了制冷片冷端温度的实际需求。在半导体制冷片的制冷应用中，对制冷片的制冷温度往往有一定要求，如半导体制冷除湿[21]过程中，制冷片冷端温度必须低于空气的露点温度；或当用于疫苗冷藏[22]时，制冷片冷端温度必须控制在一定温度下，使疫苗的温度保持2～8 ℃。

此外，以上研究大多以电流作为制冷片优化的初始条件，以电压作为优化研究的初始条件还很缺乏。原因是制冷片几何参数与制冷片冷热端温度以及输入电流之间存在耦合关系，当给定电压(非电流)时，电流从固定值变为因变量，难以从理论上分析制冷片几何参数对制冷量和COP的影响。但是，生产生活中恒压源比恒流源更常用。

因此，本文固定半导体制冷片外部的冷热端换热条件及输入电压，分别以半导体制冷量、COP及制冷片冷端温度为优化目标，来优化制冷片结构尺寸。由于冷热端温度及输入电流从固定值变为因变量，不仅增加了需要优化的过程变量及目标，还使多参量之间的耦合关系更加凸显，大大增加了确定制冷片最佳几何参数的难度。为解决这一问题，本文结合数值模拟结果，从帕尔贴效应、焦耳效应和傅里叶效应随着制冷片几何参数变化而变化的结果，分析制冷片几何参数对制冷量、制冷片冷端温度和COP的影响。综合制冷量、COP和制冷片冷端温度3个优化目标对制冷片几何参数选取范围的约束特性，提出了基于多目标优化的几何参数选择图，为今后制冷片几何参数的设计提供更加直观地参考。

1 制冷片结构设计原理

1.1 制冷片设计基本方程

制冷片根据半导体材料的热电效应进行吸热和放热，这种热电效应共由5种不同的效应组成，即塞贝克效应、帕尔贴效应、焦耳效应、傅里叶效应和汤姆逊效应。本文考虑前4种效应并忽略汤姆逊效应的影响。以半导体制冷系统(图2)为分析对象，系统方程为：

(1)

Qc=N(αp-αn)ITc-1 000NI2ρLA-

(2)

(3)

U=N[2 000IρLA+(αp-αn)(Th-Tc)]

(4)

(5)

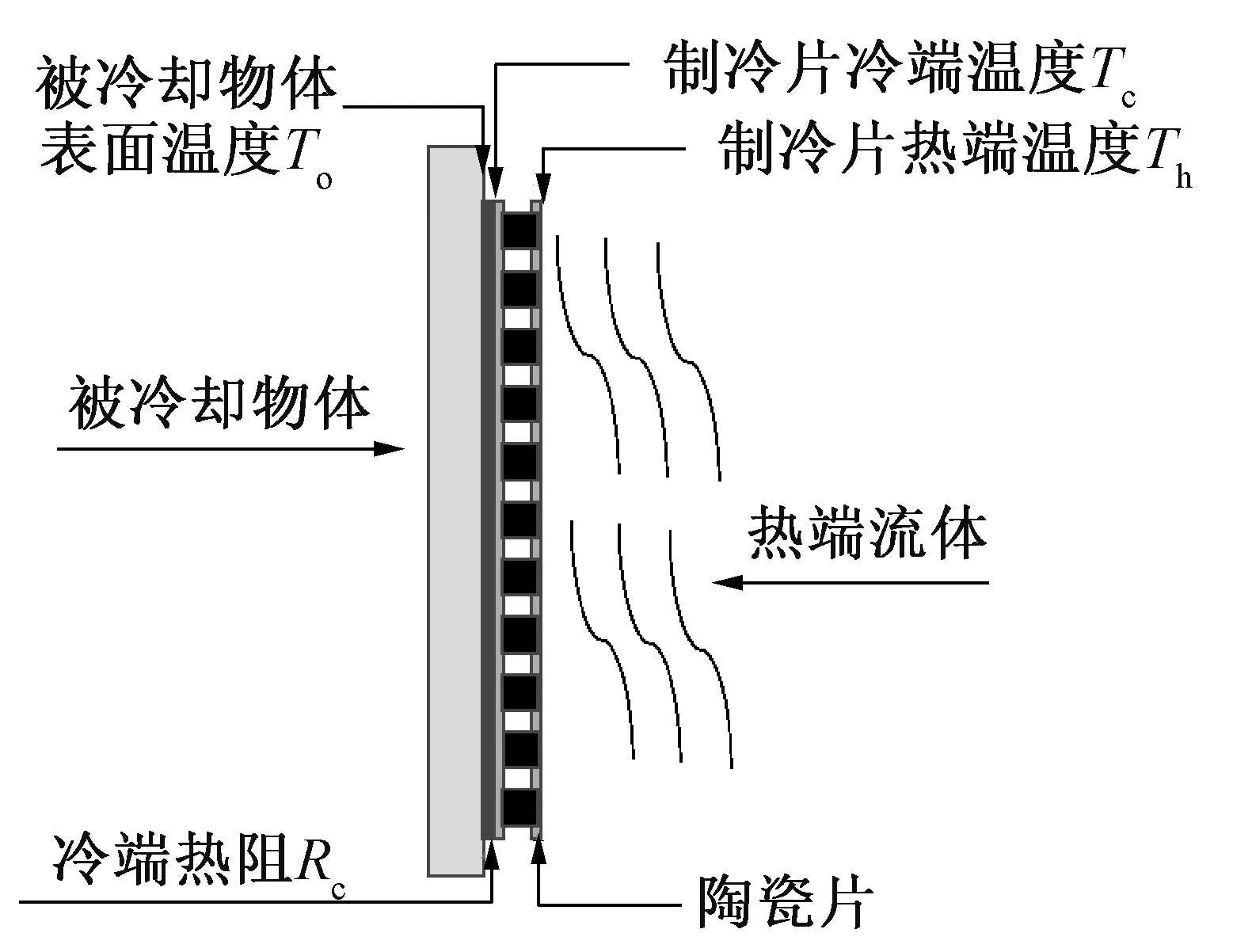
图2 制冷片系统Fig.2 System of a thermoelectric cooler

在以上方程的建立过程中采用了以下假设(与实际生产加工情况相符)：1)p结和n结的热电偶几何参数一致；2)p结和n结的电阻率、热导率和塞贝克系数绝对值相同，且与温度无关；3)p结和n结的热电偶截面为正方形。

1.2 制冷片的设计环境

基于制冷片可能的应用环境，对半导体物性及冷热端运行条件(冷热端热阻、表面积、电压等)相关参数进行初始设置[1]，如表1所示。即使在实际应用中冷热端运行条件不同于本文的设置，此优化分析方法依然适用。

冷端热阻和热端热阻是由制冷片表面积和冷热端传热系数得到的，在实际制冷片应用中，冷端一般与被冷却物体紧贴，传热方式为导热，为了使被冷却物体表面温度可以均匀分布，在本文中认为冷端的导热材料为铝，导热系数为237 W/(m·K)，铝的厚度为1 cm，相当于冷端传热系数为23.7 kW/(m2·K)。热端采用对流的方式进行换热，表面传热系数为1.2 kW/(m2·K)；得出冷热端的传热热阻；另外，为了防止制冷片表面带电，在pn结的两端分别加上很薄的陶瓷片，忽略热阻及系统中各物体间的接触热阻。

表1 半导体制冷系统参数初始设置Tab.1 Initial setting of thermoelectric coolingsystem parameters

本文的优化自变量为制冷片几何参数，分别为pn结的对数N和pn结高度与截面积之比LA，其中LA=L/A，L为pn结的高度，A为p结(或n结)的截面积。由于公式中pn结高度与截面积总是以相除的形式存在，为了方便计算，变量LA常用来统一表征高度和截面积对制冷量的影响[13]。

根据pn结实际的加工工艺，针对长宽都为10 cm(S=0.01 m2)的正方形半导体制冷片，N的值域为(0，2 500)，LA的值域为(0，10)。

在制冷片热端侧设置298 K的散热流体(如室温水)，流速恒定以维持表1所示的热端换热热阻。在稳态时，制冷片的制冷量Qc与被冷却物体的发热量Qw相匹配，对制冷片系统完成边界条件的设置。为防止计算中出现制冷片相关参数违背实际物理意义，需对制冷片的热端温度和冷端温度设置相应的约束条件：1)制冷片冷端温度Tc≤298 K；2)制冷片热端温度Th≥298 K。这样可以体现制冷片冷却相对散热流体直接接触冷却的优势，避免在计算中出现Tc高于Th的错误。

1.3 模型的验证

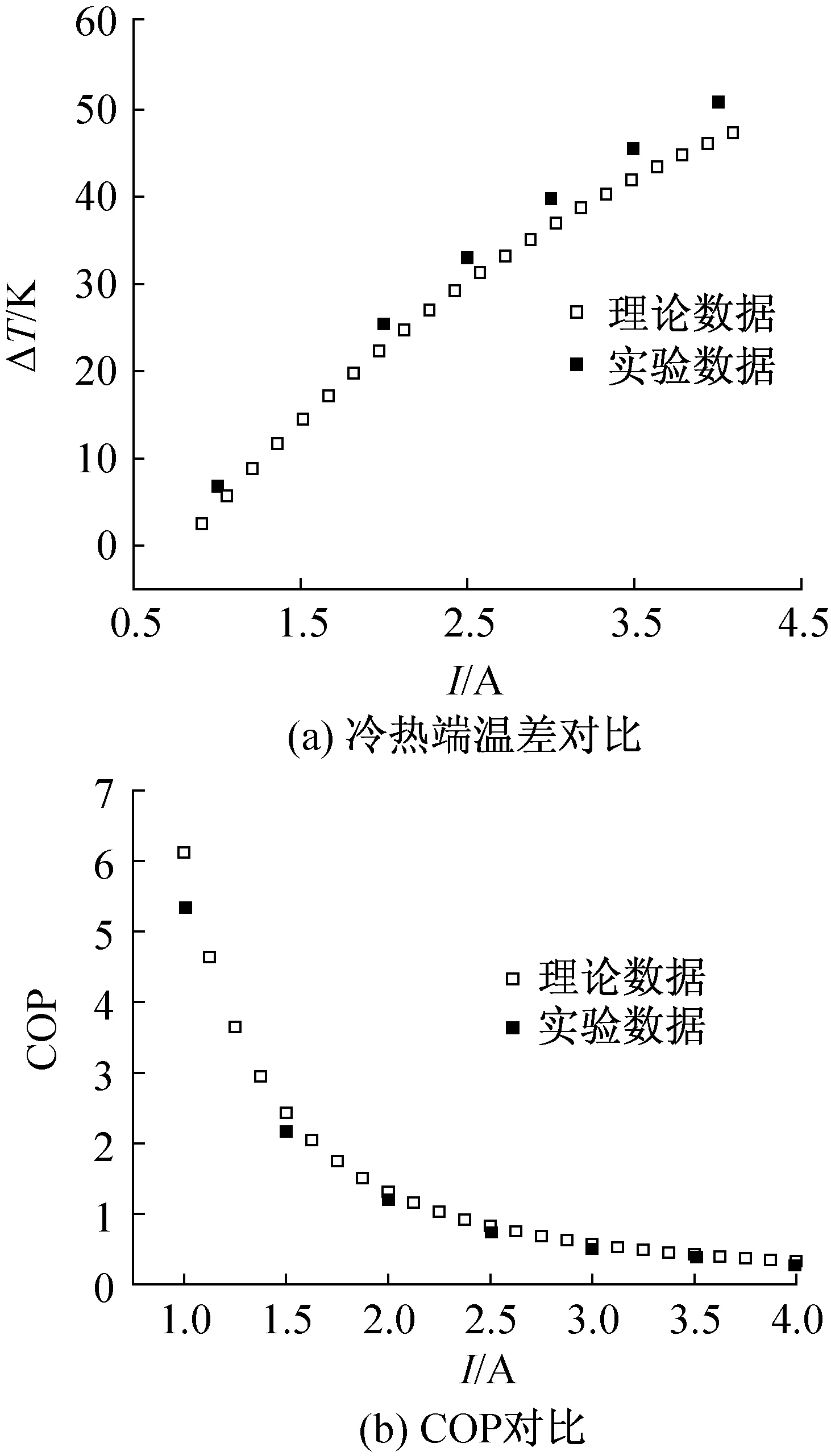
图3 理想模型制冷效果与实验制冷效果的对比Fig.3 The comparison between cooling effect simulatedby the ideal model and experimental results

本文针对半导体的热电效应建立的理想模型，视塞贝克系数为常数，忽略了汤姆逊效应带来的影响。为了研究忽略汤姆逊效应对半导体制冷效果影响，根据文献[23]的实验条件：Th=343.2 K，Qc=12.3 W，αpn=0.000 378 V/K，k=2.571 W/(m·K)，ρ=0.000 01(Ω·m)，LA=1.02(1/mm)，N=125。图3所示为理想模型制冷效果与实验制冷效果的对比，发现两者吻合较好。因此，本文采用的理想模型可以很好地预测或反映半导体制冷的实际情况。

2 结构参数的影响

表1共有7个已知参数，式(1)～式(5)中，有8个未知量，分别为热电偶的高度与横截面面积的比LA，pn结的对数N，电流I，制冷片冷端温度Tc，制冷片热端温度Th，被冷却物体的发热量Qw(或制冷片的制冷量Qc)，被冷却物体的表面温度To和整个系统的COP。研究N(或LA)对Qc最大值影响时，给定Tc、LA(或N)，并让N(或LA)取不同的值，这样还有5个未知量对应5个方程，实现方程的封闭性；研究N(或LA)对Tc最小值和COP影响时，给定Qw、LA(或N)，并让N(或LA)取不同的值，可实现方程的封闭性；然后利用EES软件，在相应的参数设置条件下，对上述方程组进行仿真求解。

2.1 N对Qc最大值、Tc最小值和COP的影响

为了获得Qc的最大值，Tc越大越好。因为Tc越大，冷端帕尔贴效应越强，且制冷片冷热端温差越小，傅里叶导热效应越差，制冷量越大。在理论极限上，Tc可以等于Th，但根据前文分析，Tc的最大值为298 K，则取Tc=298 K；求解式(1)～式(5)，可得N对Qc最大值的影响规律，如图4所示，该规律可用式(2)来解释。

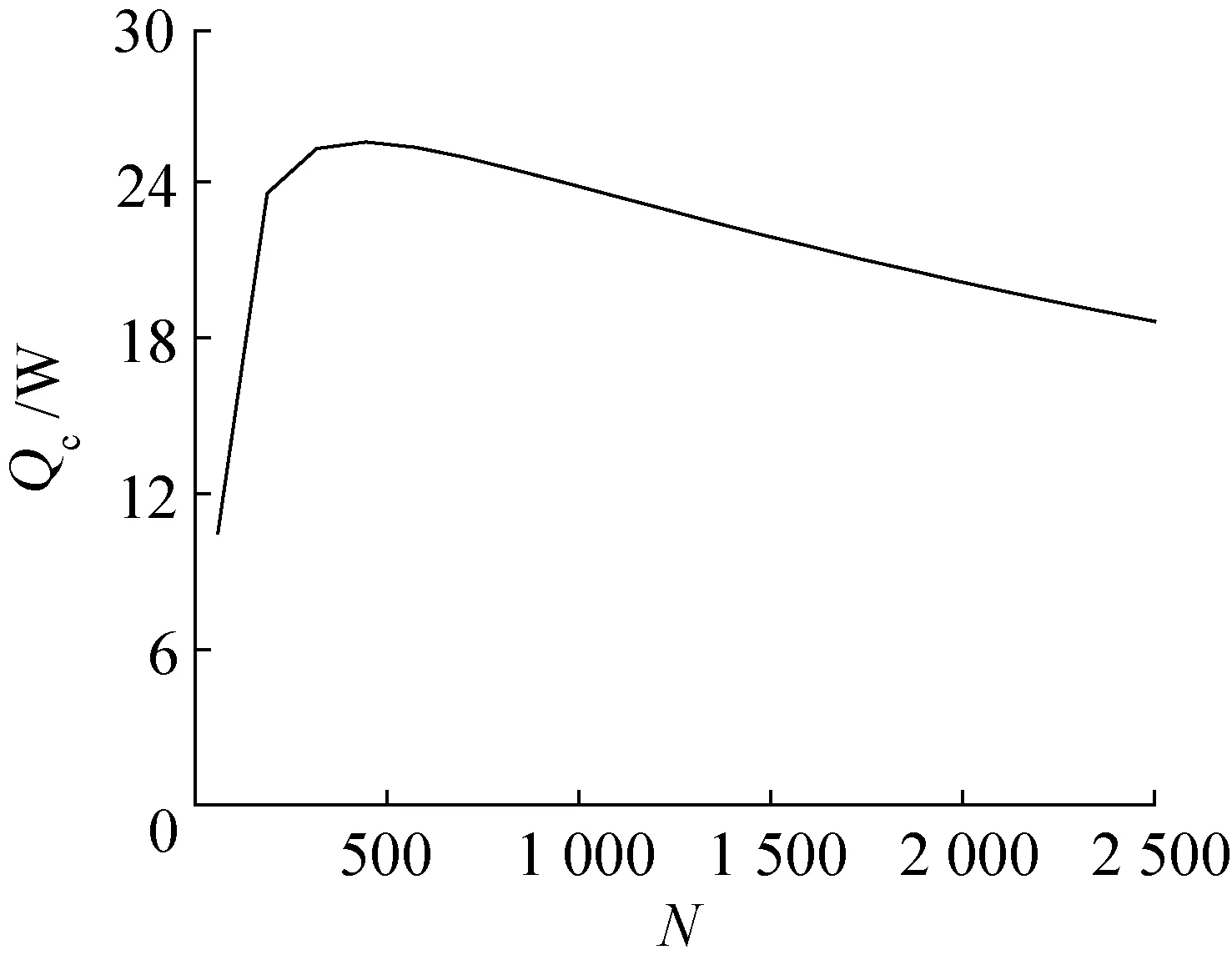
图4 在LA和Tc给定情况下，N对Qc最大值的影响Fig.4 Given LA and Tc, the effect of N on the maximum value of Qc

给定LA和Tc，随着N的增大，由于N对pn结串联连接，制冷片的电阻增大，则pn结中的I逐渐降低(图5)，等式右边表征冷端帕尔贴效应的第一项和焦耳热效应的第二项都会随电流降低而降低。由于电流减小，制冷片热端载流子迁移速率降低，放热能力降低，此时外界流体(室温水)带走热量的能力大于载流子放热能力。由于两者最终实现平衡，因此Th下降，制冷片热端帕尔贴效应降低，同时焦耳热效应降低。Th主要由帕尔贴效应和焦耳热决定，Th的逐渐降低使表征傅里叶效应的第3项也降低(图6)。由于帕尔贴效应在热电效应中占主导地位，所以单对pn结的制冷量降低(图7)。总制冷量是pn结个数N和单个pn结制冷量的乘积，图6中，当N较小时，N的增大速率比pn结制冷量的降低速率大。因为N从50增大到500时，N值扩大10倍，而单个pn结制冷量从0.128 W降低到0.04 W，只降低2.56倍，因此整个制冷片制冷量表现为增大。当N较大时，N的增大速率比pn结制冷量的降低速率小，因为N从1 500增大到2 000时，N值只扩大1.3倍，而单个pn结制冷量从0.014 W降低到0.01 W，降低1.4倍，导致整个制冷片制冷量表现为降低。值得注意的是这一点与从图7上获取的直观感受存在差异。综上所述，制冷片的最大制冷量随着N值的增大先增大后降低(图4)。

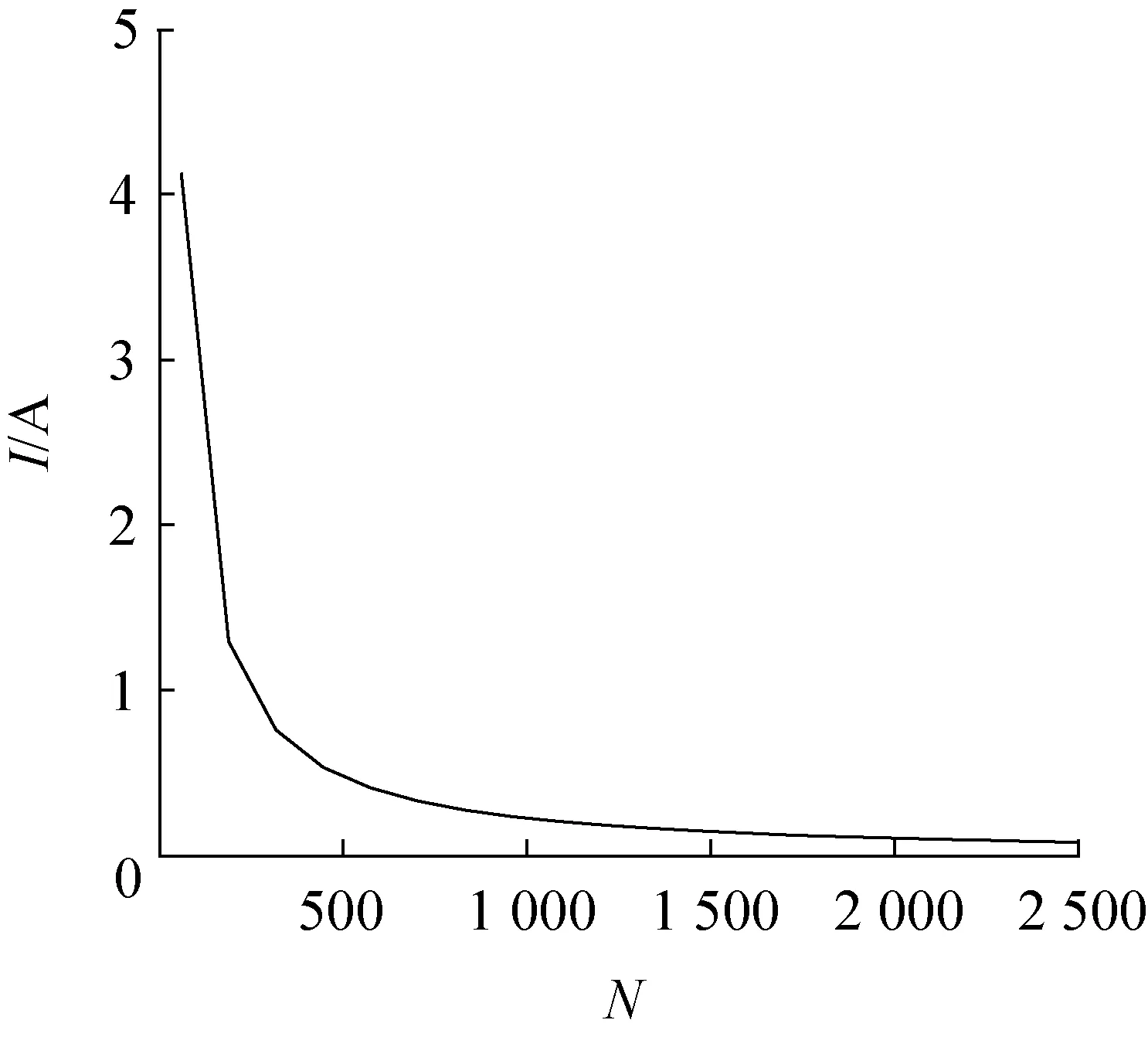
图5 在LA和Tc给定情况下，N对I的影响Fig.5 Given LA and Tc, the effect of N on current

图6 在LA和Tc给定情况下，N对傅里叶效应的影响Fig.6 Given LA and Tc, the effect of N on the Fourier effect

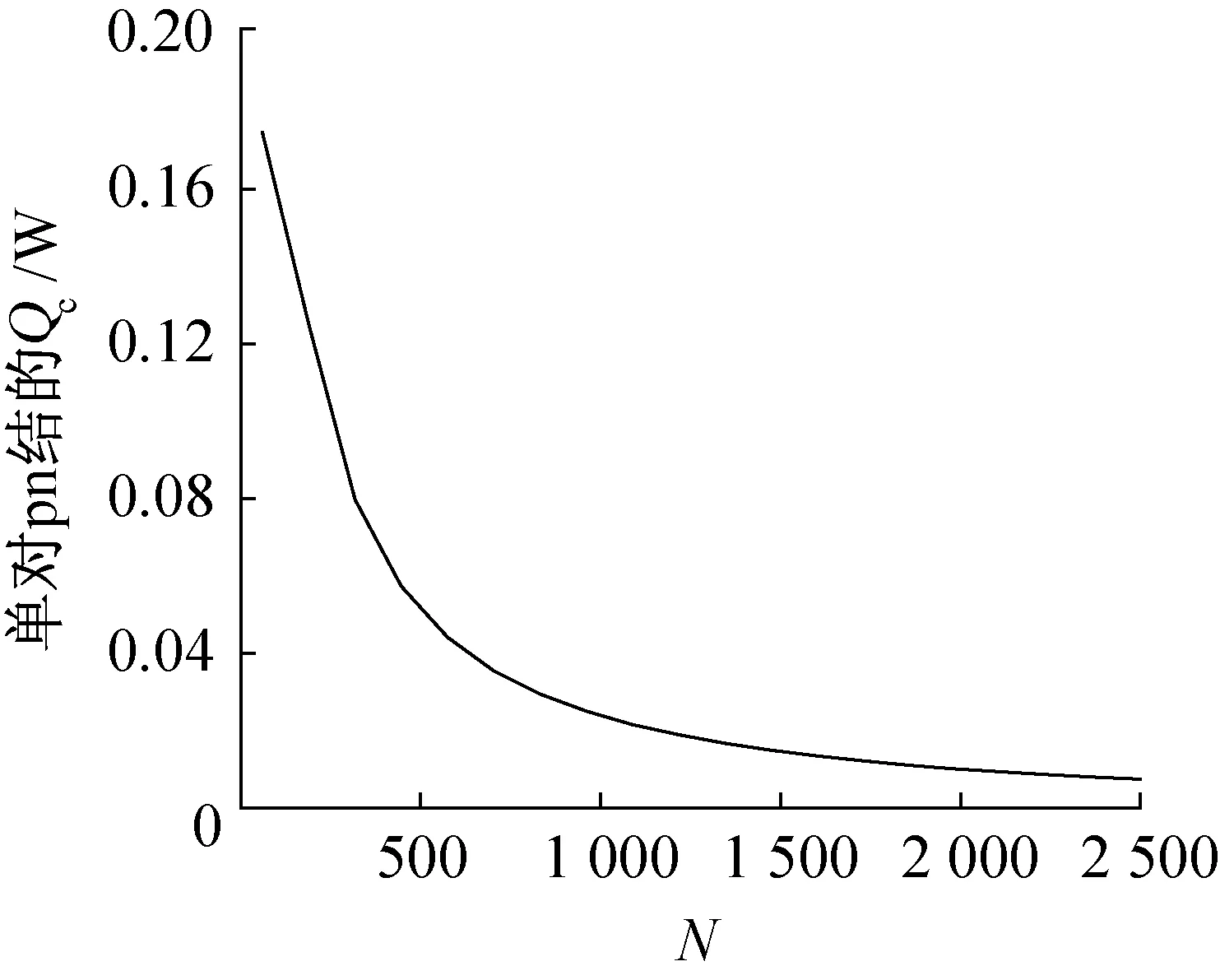
图7 在LA和Tc给定情况下，N对单对pn结制冷量的影响Fig.7 Given LA and Tc, the effect of N on the cooling capacity of single-pair thermoelectric cooler

给定Qw和LA，计算可得N对Tc的影响规律。N对Tc的影响规律如图8所示，将式(4)带入式(2)中，可以发现Tc与N和I的关系式(6)：

αpnITc=1 000I2ρLA+

(6)

式(6)是针对单对pn结而言，表征了取冷端表面为控制面上的能量守恒。等式左边表征制冷片冷端的帕尔贴热，即从冷端表面带走的热量。等式右边是输入到冷端表面的热量，第一项表征由焦耳热效应引起的传向制冷片冷端的热量；等式右边第二项表征了因傅里叶传导效应而传向制冷片冷端的热量，等式右边第三项表征pn结冷端从外界吸收的热量。

图8 在Qw和LA给定情况下，N对Tc的影响Fig.8 Given LA and Qw, the effect of N on temperature of cold end of thermoelectric cooler

为更加清晰地表达Tc与N和I的关系，对式(6)两边约去一个I得到式(7)：

αpnTc=1 000IρLA+

(7)

由图9可知，I随着N的增大而降低，即焦耳热效应降低，采用与图7中相同的分析方法可得N与I的乘积随着N增大而减小，傅里叶效应增大但增大不明显；同理，从外界吸热效应也会增大。由于当N较小时，相比傅里叶效应和外界吸热效应的增大，焦耳热效应降低的更多；当N较大时，相比傅里叶效应和外界吸热效应的增大，焦耳热效应降低的少。因此，随着N的增大，制冷片冷端帕尔贴效应先降低后增大，即制冷片冷端温度先降低后增大。

图9 在Qw和LA给定情况下，N对I的影响Fig.9 Given LA and Qw, the effect of N on current

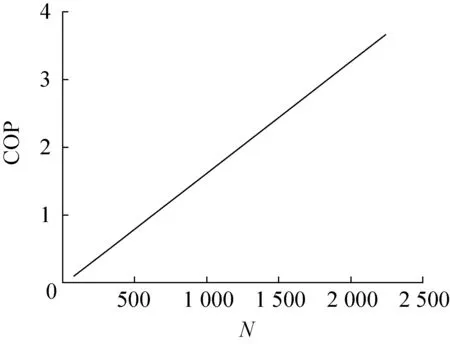
图10 在LA和Qw给定情况下，N对COP的影响Fig.10 Given LA and Qw, the effect of N on COP

给定Qw和LA，计算可得N对COP的影响规律。N对COP的影响规律如图10所示，COP随着N的增大而增大。N的增大，使I降低(图9)，即在输出冷量不变时，输入功率变小，COP一直增大。但N值受一定约束，不可以无限增大。N值的约束来自两个方面：1)实际加工工艺的约束，一定表面积的陶瓷片上承载的pn结必然存在一个最大值；2)制冷量的约束，因为最大制冷量会随着N值的增大先增大后降低，所以为了实现一定的制冷量，N值必然只能在一定范围内变化。此外，当N值较大时，各对pn结之间横向的热传递更明显，影响整个制冷片的传热模型，COP与N之间的关系也发生改变。但本文没有考虑各对pn结之间横向的热传递，所以N对COP的影响较理想化。

2.2 LA对Qc最大值、Tc最小值和COP的影响

取Tc=298 K，LA对Qc最大值的影响规律由式(2)可知，如图11所示。

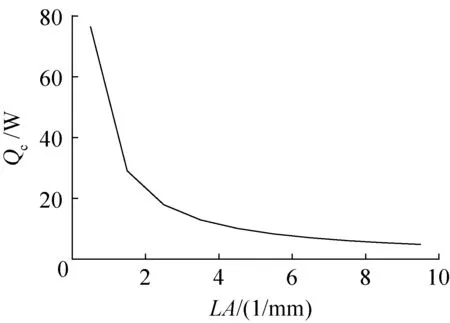
图11 在N和Tc给定的情况下，LA对Qc最大值的影响Fig.11 Given N and Tc, the effect of LA on the maximum value of Qc

如3.1节所述，为了获得Qc的最大值，给定N值时，Tc应为298 K；随着LA的增大，pn结中的I逐渐降低(图12)，由于制冷片冷端温度Tc不变，冷端帕尔贴效应逐渐降低；采用与图7相同的分析方法，分析图12可知，随着LA的增大，I的平方与LA的乘积降低，焦耳热效应降低；此时制冷片冷热端的温差ΔT(Th-Tc)逐渐变小(图13)，因此LA的增大会使傅里叶效应降低；由于帕尔贴效应在热电效应中占主导地位，所以单对pn结的制冷量一直降低，因而制冷片的最大制冷量也一直降低。

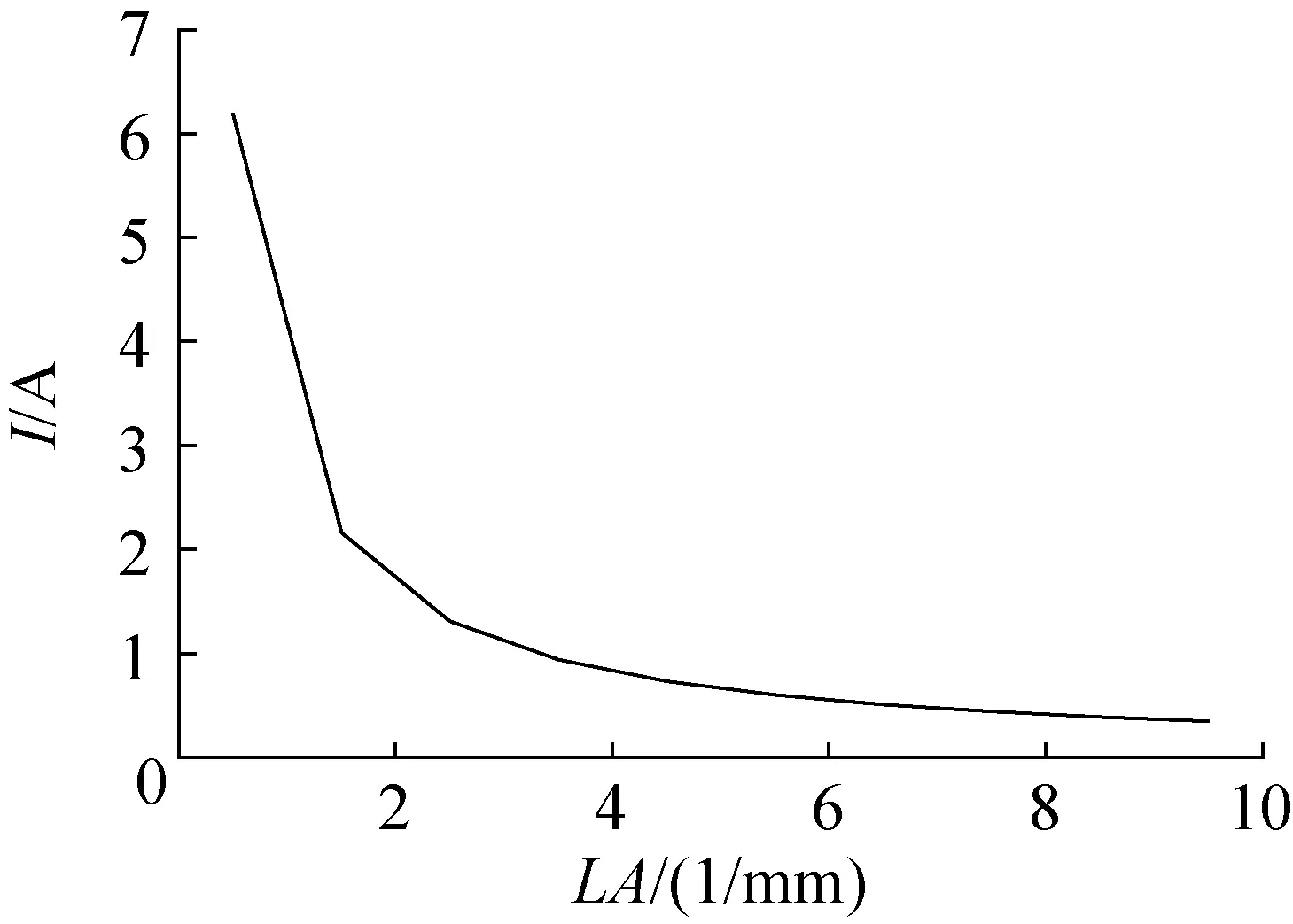
图12 在N和Tc给定的情况下，LA对I的影响Fig.12 Given N and Tc, the effect of LA on current

LA对Tc的影响规律由式(7)可知，如图14所示。

由图15可知，给定N和Qw，随着LA的增大，I逐渐降低，LA的增大速率比I的降低速率大，使焦耳热效应增大；同理，LA与I的乘积变大，导致傅里叶效应降低；由于I的降低，从外界吸热效应也增大。当LA较小时，相比焦耳热效应和外界吸热效应的增大，傅里叶效应降低的更多；在LA较大时，相比焦耳热效应和外界吸热效应的增大，傅里叶效应降低的较少。因此随着LA的增大，制冷片冷端帕尔贴效应会先降低后增大，即制冷片冷端温度Tc先降低后增大。

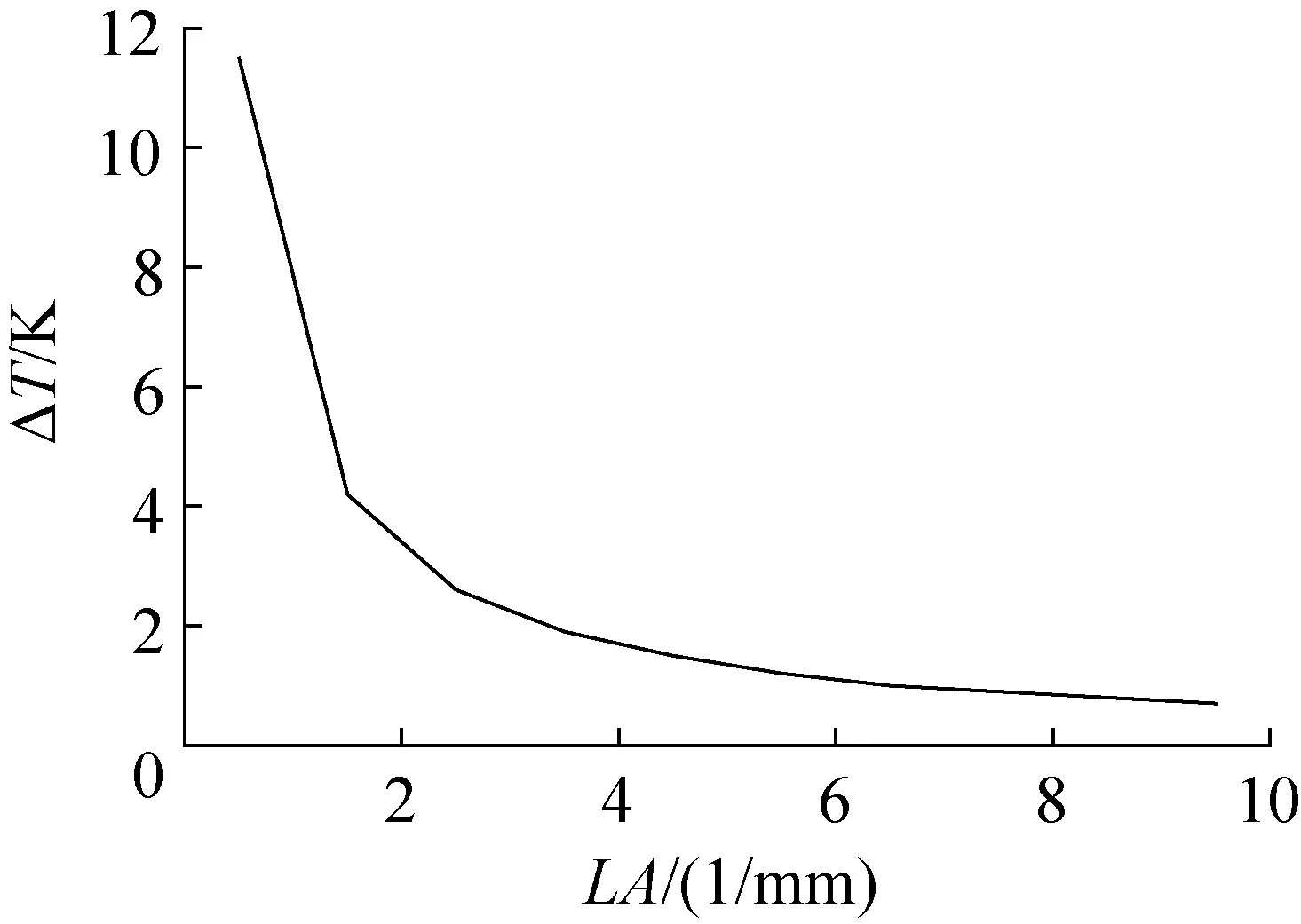
图13 在N和Tc给定的情况下，LA对制冷片冷热端温差ΔT的影响Fig.13 Given N and Tc, the effect of LA on the temperature difference ΔT

图14 在N和Qw给定情况下，LA对Tc的影响Fig.14 Given N and Qw, the effect of LA on temperature of cooled object

图15 在N和Qw给定情况下，LA对I的影响Fig.15 Given N and Qw, the effect of LA on current

给定N和Qw，LA对COP的影响规律如图16所示，随着LA的增大，I逐渐降低(图15)，又由于Qc和U不变，因此COP一直增大。

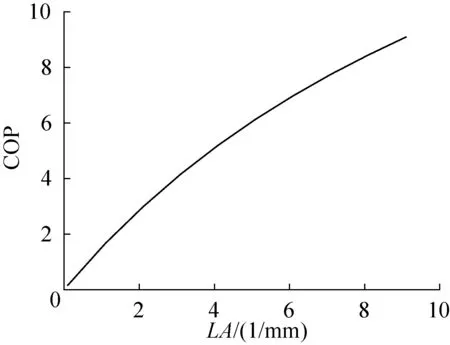
图16 在N和Qw给定情况下，LA对COP的影响Fig.16 Given N and Qw, the effect of LA on COP

3 多目标约束下半导体制冷片几何参数的优化

前文研究了在给定电压、换热条件及制冷片表面积的情况下，N和LA对Qc最大值、Tc最小值和COP的影响。在上述分析过程中，为了使方程可解，Qc或Tc的值必须假定其中一个。在实际应用中，对于制冷片而言，不仅想获得最大的制冷量，或最低的表面温度，或最大的COP，更希望制冷片既能提供所需的制冷量，冷端又能保持一定的温度，使被冷却物体在合适的温度下运行实现节能，即往往是约束过多的情况，但约束过多可能导致无解。本文将进一步分析如何在多目标约束下，对制冷片几何参数进行优化。

3.1 不同设计目标下最佳几何参数的确定

为了分析在制冷片几何参数优化这一特定的应用中，约束过多是否仍然存在特定解，本节将根据不同的设计目标，计算相应的最佳制冷片几何参数。在给定电压、换热条件及制冷片表面积，以制冷片制冷量为优化目标时，基于前文制冷片几何参数对制冷量影响的研究结果可知，Qc随着N的增大先增大后降低，随着LA的增大一直降低。当要求Qc不小于一定值时，N的取值范围随着LA的增大而缩小且LA的取值范围会被限定在0.1到某一个值内，从而使N和LA的取值范围在几何参数选择图上围成一个四边形。假设给定制冷片制冷量优化目标为15 W，经计算得出，当N在70～2 400且LA在0.1～2.8这个四边形范围内任何一点均能满足该制冷量的优化目标，如N=1 200，LA=1.5或N=1 200，LA=2.8，只是不同N或LA取值，对应的冷端温度不同。当以制冷片冷端温度为优化目标时，基于前文制冷片几何参数对制冷片冷端温度影响的研究结果可知，Tc随着N的增大先降低后增大，Tc随着LA的增大先降低后增大，那么当要求Tc不高于一定值时，N和LA都会被限定在有限的取值范围内，从而围成一个四边形。假设给定制冷片冷端温度的优化目标为280 K，经计算得出，当N在50～400且LA在0.1～10这个四边形范围内任何一点均能满足该优化目标，如N=200，LA=3或N=300，LA=5，只是不同N或LA取值，对应的制冷片冷量不同。研究发现，当分别以制冷量和制冷片冷端温度为目标时，得出的制冷片结构参数范围存在一定的区别，说明不同的优化目标有不同的最佳结构参数范围，因此一种优化目标的优化结果并不一定适用于另一种优化目标。但是，各目标优化的结果存在交集，即存在一定的结构尺寸范围能满足多个优化目标，多目标约束下，仍然存在特定解，为下文提出多目标优化的几何参数选择图提供了可能。当优化目标为COP时，由上述的LA和N对COP的影响规律可知，为了获取最大的COP，LA和N都应该选择值域中的最大值，因此该优化结果不再是一个范围而是一个点。可知该优化目标为上述优化目标下的最佳几何参数从一个范围缩小至一个点提供了可能。

3.2 多目标约束下最佳结构参数的确定

基于多目标约束的情况，需要提出如图17所示的多目标优化的几何参数选择图。

图17 多目标优化的几何参数选择图Fig.17 Multi-objective optimization of the geometric parameters based on the selecting map

图17(a)是以制冷量为15 W、制冷片冷端温度为280 K且COP最大为目标时的制冷片几何参数选择图。其中虚线四边形是由制冷量确定的，将需要的制冷量代入程序中，解出所有可能提供所需制冷量的制冷片几何参数组合，绘制近似四边形。实线四边形是由制冷片冷端温度确定的，同理，将要求的冷端温度输入程序中，解出所有可能满足制冷片冷端温度要求的制冷片几何参数组合，绘制近似四边形。圆点由最大COP确定，由于COP随着N和LA的增大而增大，因此N和LA值最大的交叉处COP最大，从而确定最节能的点。该点对应的几何参数可满足多目标约束要求的最佳制冷片几何参数。

根据与图17类似的多目标优化几何参数选择图能快速判断制冷片几何参数的改变能否满足制冷量和制冷片冷端温度的要求。如果以制冷量和制冷片冷端温度为目标的两个四边形没有交叉区域(图17(b))，说明在现有的电压及制冷片冷热端散热条件下，制冷片在制冷温度(240 K)下无法提供相应的制冷量(100 W)。说明在这两个目标下，无论怎么改变制冷片的几何参数，均无法同时实现相应的目标。采用这样的设计和选型方法，为制冷片结构参数的改变能否满足相应目标提供了一种快速判断的依据，也极大地提高设计者的设计和选型效率。

4 结论

传统的半导体制冷片几何参数优化研究，都是基于给定制冷片自身的冷热端温度，研究其对制冷量和COP的影响，和现实应用情况难以直接对应。本文基于制冷片外部换热条件固定的情况，不仅以制冷量和COP为优化目标，还以常被忽略的制冷片冷端温度为优化目标，为在换热热阻受限制条件下的制冷片进行几何参数优化设计。在本文的约束条件下，当所需制冷量明确时，为优化COP，几何参数的变化导致制冷片冷端温度发生变化。同理，当所需冷端温度明确时，几何参数的变化同时影响制冷量和COP。在实际应用中，如果对制冷量、COP和冷端温度同时提出要求，则属于多目标约束下的优化要求。

为研究多目标约束的优化方法，本文分析了在给定电压、换热条件及制冷片表面积的情况下，制冷片几何参数分别对制冷量、COP和制冷片冷端温度的影响，对每个影响项的物理含义给出详细说明。并综合制冷量、COP和制冷片冷端温度3个优化目标对制冷片几何参数选取范围的约束特性，提出基于多目标优化的几何参数选择图，为今后制冷片几何参数的设计提供直观地参考，得到如下结论：

1) 在给定电压、换热条件及制冷片表面积的情况下，当LA和Tc不变时，Qc随着N的增大先增大后降低；当LA和Qc不变时，Tc随着N的增大先降低后增大，COP随着N的增大而增大。

2) 在给定电压、换热条件及制冷片表面积的情况下，当N和Tc不变时，Qc随着LA的增大一直降低；当N和Qc不变时，Tc随着LA的增大先降低后增大，COP随着LA的增大而增大。

3) 在给定电压、换热条件及制冷片表面积的情况下，针对制冷片有不同的设计目标时，得出的结构尺寸范围不同，但不同目标下的结构参数可能存在交集，这为本文提出多目标优化结构选择图提供了可能。

4) 在给定换热条件及制冷片表面积的情况下，通过多目标优化的几何参数选择图可以帮助设计者判断多目标约束下是否存在制冷片几何参数满足相应要求。如果存在，该图可以帮助设计者确定最佳制冷片的几何参数，为用户定制制冷片。其中制冷量和制冷片冷端温度可以确定几何参数的范围，COP有助于缩小范围，最终确定最佳的几何参数。

符号说明

Ta——制冷片热端散热流体温度，K

To——被冷却物体的表面温度，K

Tc——制冷片冷端温度，K

Th——制冷片热端温度，K

ΔT——冷热端温差，K

αp——p型半导体的塞贝克系数，V/K

αn——n型半导体的塞贝克系数，V/K

αpn——半导体材料的温差电动势率，V/K

I——电路中电流，A

ρ——p结和n结热电偶的电阻率,(Ω5m)

U——输入电压,V

Qw——被冷却物体的发热量,W

Qc——制冷片冷端吸热量,W

k——p结和n结的热导率,W/(m5K)

S——制冷片表面积,m2

Rc——制冷片冷端吸热热阻,K/W

Rh——制冷片热端散热热阻,K/W

LA——p结和n结高度与截面积之比,(1/mm)

N——pn结的对数

本文受浙江省自然科学基金(LY17E060002)项目资助。(The project was supported by Natural Science Foundation of Zhejiang Province(No.LY17E060002).)

[1] 罗仲, 张旭, 王胜己,等. 半导体制冷器除湿实验研究[J]. 制冷学报, 2015，36(5):101-106.(LUO Zhong, ZHANG Xu, WANG Shengji, et al. Experimental research on performance optimization of thermoelectric dehumidifier[J]. Journal of Refrigeration, 2015, 36(5): 101-106.)

[2] 徐德胜. 半导体制冷与应用技术[M]. 上海：上海交通大学出版社, 1992.(XU Desheng. Semiconductor refrigeration and application technique[M]. Shanghai：Shanghai Jiao Tong University Press,1992.)

[3] 王春燕, 厉彦忠, 郑江. 多级温差发电器串并联分析模型[J]. 制冷学报, 2016，37(1):106-113.(WANG Chunyan, LI Yanzhong, ZHENG Jiang. Analytical model for multi-stage thermoelectric generator with series and parallel connection[J]. Journal of Refrigeration, 2016,37 (1): 106-113.)

[4] 周兴华. 半导体制冷技术及应用[J]. 电子世界, 2000(9):52-53.(ZHOU Xinghua. Semiconductor refrigeration technology and its application[J]. Electronics World, 2000(9):52-53.)

[5] ZHOU Yuanyuan,YU Jianlin. Design optimization of thermoelectric cooling systems for applications in electronic devices[J]. International Journal of Refrigeration, 2012, 35(4):1139-1144.

[6] TAYLOR R A, SOLBREKKEN G L. Comprehensive system-level optimization of thermoelectric devices for electronic cooling applications[J].IEEE Transactions on Components & Packaging Technologies, 2008, 31(1):23-31.

[7] DAI Y J, WANG R Z, NI L. Experimental investigation and analysis on a thermoelectric refrigerator driven by solar cells[J]. Solar Energy Materials and Solar Cells, 2003, 77(4): 377-391.

[8] ABDUL-WAHAB S A, ELKAMEL A, AL-DAMKHI A M, et al. Design and experimental investigation of portable solar thermoelectric refrigerator[J]. Renewable Energy, 2009, 34(1):30-34.

[9] DAI Y J, WANG R Z, NI L. Experimental investigation on a thermoelectric refrigerator driven by solar cells[J]. Acta Energiae Solaris Sinica, 2003, 28(6):949-959.

[10] CHENG Y H, LIN W K. Geometric optimization of thermoelectric coolers in a confined volume using genetic algorithms[J]. Applied Thermal Engineering, 2005, 25(17/18): 2983-2997.

[11] FRAISSE G, LAZARD M, GOUPIL C, et al. Study of a thermoelement′s behaviour through a modelling based on electrical analogy[J]. International Journal of Heat & Mass Transfer, 2010, 53(17/18):3503-3512.

[12] MIN G, ROWE D M. Improved model for calculating the coefficient of performance of a Peltier module[J]. Energy Conversion and Management, 2000, 41(2): 163-171.

[13] HUANG Yuxian, WANG Xiaodong, CHENG Chinhsiang, et al. Geometry optimization of thermoelectric coolers using simplified conjugate-gradient method[J]. Energy, 2013, 59:689-697.

[14] ZHU Wei, DENG Yuan, WANG Yao, et al. Finite element analysis of miniature thermoelectric coolers with high cooling performance and short response time[J]. Microelectronics Journal, 2013, 44(9):860-868.

[15] WANG C C, Hung C I, Chen W H. Design of heat sink for improving the performance of thermoelectric generator using two-stage optimization[J]. Energy, 2012, 39(1):236-245.

[16] GAO Xin, CHEN Min, SNYDER G J, et al. Thermal management optimization of a thermoelectric-integrated methanol evaporator using a compact CFD modeling approach[J]. Journal of Electronic Materials, 2013, 42(7):2035-2042.

[17] WANG Xiao, YU Jianlin, MA Ming. Optimization of heat sink configuration for thermoelectric cooling system based on entropy generation analysis[J]. International Journal of Heat & Mass Transfer, 2013, 63(5):361-365.

[18] ZHU Lin, TAN Hongbo, YU Jianlin. Analysis on optimal heat exchanger size of thermoelectric cooler for electronic cooling applications[J]. Energy Conversion & Management, 2013, 76(30):685-690.

[19] PAN Yuzhuo, Lin Bihong, Chen Jincan. Performance analysis and parametric optimal design of an irreversible multi-couple thermoelectric refrigerator under various operating conditions[J]. Applied Energy, 2007, 84(9):882-892.

[20] ZHANG H Y. A general approach in evaluating and optimizing thermoelectric coolers[J]. International Journal of Refrigeration, 2010, 33(6):1187-1196.

[21] MILANI D, ABBAS A, VASSALLO A, et al. Evaluation of using thermoelectric coolers in a dehumidification system to generate freshwater from ambient air[J]. Chemical Engineering Science, 2011, 66(12):2491-2501.

[22] PUTRA N. Design, manufacturing and testing of a portable vaccine carrier box employing thermoelectric module and heat pipe[J]. 2009, 33(3):232-237.

[23] DU C Y, WEN C D. Experimental investigation and numerical analysis for one-stage thermoelectric cooler considering Thomson effect[J]. International Journal of Heat & Mass Transfer, 2011, 54(23/24):4875-4884.