浅析卡诺图化简逻辑函数

刘中旭

【摘要】在学习数字逻辑课程时，经常需要对逻辑函数进行化简。化简时，一种方法是使用布尔代数的定律进行化简，另一种方法是使用卡诺图进行化简。第一种方法要求准确掌握布尔代数定律和一些化简技巧，第二种方法则相对简单。

【关键字】卡诺图 化简

一、卡诺图介绍

卡诺图是由美国贝尔实验室的电信工程师莫里斯·卡诺（Mau-rice Karnaugh）在1953年根据维奇图改进而来的，它是一种平面方格图。1任何一个逻辑函数都可以化为一组最小项之和的表达式，每一个最小项对应卡诺图中的一个方格。图1和图2分别为三变量和四变量的卡诺图。每一个最小项用m加上下标表示，下标为最小项编号对应的二进制数转化为十进制数。原变量取值1，非变量取值0，例如ABC编号为110，用m₆表示。

二、逻辑函数在卡诺图中的表示

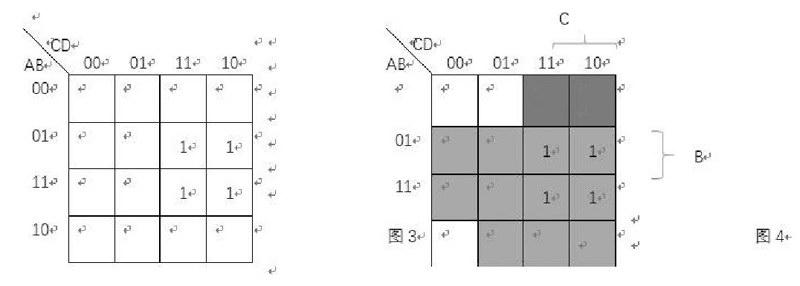
虽然卡诺图中的一个方格表示逻辑函数的一个最小项，但在将逻辑函数填写入卡诺图中时，不一定需要将逻辑函数化成最小项之和的表达式。例如F=BC，如果化为最小项之和的形式为F=BC（A+A）（D+D）=A BCD+A BCD+ABCD+ABCD，然后在卡诺图中表示将A BCD、A BCD、ABCD和ABCD的方格填写1，转化过程较为繁琐，如图3。在熟悉卡诺图结构后，可以直接填写，省去转化为最小项之和的过程，B表示卡诺图中第2、3行，C表示第3、4列，重合的区域即为BC，如果图4。

三、卡诺图化简规则和步骤

用卡诺图化简逻辑函数时，首先要找到2n个相邻最小项（为1的方格）的组合，用圈包围；圈中的为1方格的数目尽量要大；每个组合中至少一个为1方格是其他组合没有的：先画大圈，再画小圈，圈尽量少，直到所有为1的方格都被圈包围。如果1个圈里面有2n个相邻最小项，则可以消去n个变量。在找相邻最小项时，除了几何上相邻，还包括逻辑上相邻，即在卡诺图中最上面和最下面的行、最左侧和最右侧的列是逻辑上相邻的。图5中，4个圈所包围的最小项均是几何上相邻。图6中的有2个圈，上下组成一个圈，左右组成一个圈，每个圈内的最小项是逻辑相邻的。

例：用卡诺图化简F=ABCD+ABCD+AB+AD+ABC。这是一个4变量的逻辑函数，首先先画出4变量的卡诺图，把化简函数的各项填入卡诺图中：然后根据化简规则和步骤画圈，最下面4个为1的方格用一个圈包围，用AB表示，最左列和最右列的4个为1的方格用一个圈包围，用AD表示，总共用了2个圈，因此F=AB+AD，如图7。

对于4变量及以下的逻辑函数化简而言，卡诺图化简是一种较为简便的方法，值得注意的是在有些情况下，因圈法的不同，得到的化简结果不一样，即一个逻辑函数的最简与或表达式不是唯一的。

参考文獻：

[1]白中英，谢松云数字逻辑[M].北京：科学出版社，2013