基于小Higgs理论的简单模型下中微子、电子散射计算与数值分析

张凤，丁俊玲，田宇，王旭丹，吉莉

（大连科技学院辽宁大连116052）

标准模型（SM）可在低能状态下，完全描述弱、电、强间相互作用，且理论值与实验验证数据高度吻合。尽管如此，该种成熟理论仍存在无法解决的问题，如自由参数过多、存在不自然性、缺乏高能SM扩展的新物理部分等。随着粒子物理的不断演进，部分实验测量与SM预测值不符，使得高能粒子问题逐渐凸显[1-3]。于是学界致力探索新的粒子理论或模型，对其进行补充，中微子就是其中代表性的发现。

电子中微子的散射过程也称之为纯轻子反应过程，中微子间相互作用导致核子β衰变呈非分立特性。这一震荡现象一度引起研究重视，因此现象背后也许隐藏着标准模型外的粒子作用[4-5]。本文在此基础上，对SM中νee-νee过程的微分及振幅截面进行了归类分析，讨论相关参数的波动。并据此总结高能部分的νee-νee一般散射规律，推算相关参数的计算和影响因素。从而得出了中微子震荡轻子数不守恒导致的质量问题，为标准粒子模型扩展与修正提供了突破口。

1　中微子与νee电子散射过程

对于中微子的实验，在过去已进行了诸多方向的尝试，如著名的太阳中微子实验、大气中微子实验、加速器中微子震荡实验等[6]。我国也从核反应堆中微子实验中寻找突破，如大亚湾中微子实验：基于核能反应堆开展粒子实验，技术成熟、资金消耗低、周期短，且平台优势明显。

这些实验数据的积累证实了中微子震荡的现象，为了深入理解震荡的机理，需要进一步分析散射过程的相关参量，并对标准模型进行扩展，称之为“非标准作用（NSI）”。由中微子和电子散射产生的截面较小，导致测量难度倍增[7]。科学界研究出基于SU（2）L*U（1）γ的 SM 理论，实现低能状态下散射界面差异比较，从而揭示了中微子震荡的核心本质。

1.1　标准模型树的νee散射截面

标准模型下，散射过程大致可归为三类：荷电流过程、弱中性电流过程、荷电流与弱中性电流交互过程[8-9]。以下对不同过程的微分散射截面进行分析：

1）荷电流过程

振幅：

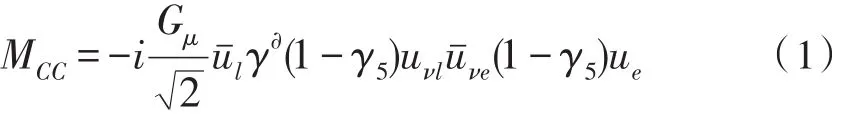
微分截面：

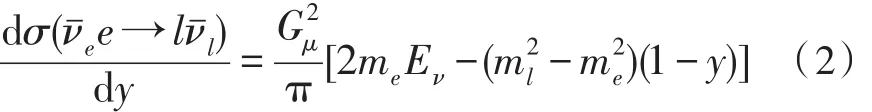
在积分值趋近于0时，总的散射截面为

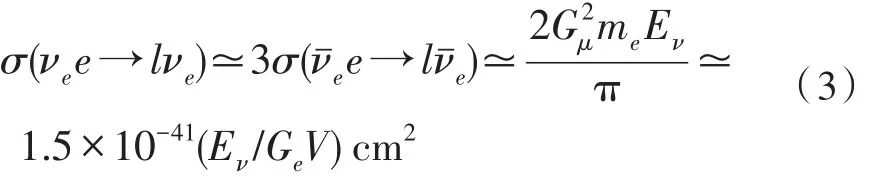
2）中性流过程

纯中性流过程，同上述分析方法，其有效振幅

其微分散射截面νle→νle和νˉle→νˉle分别为

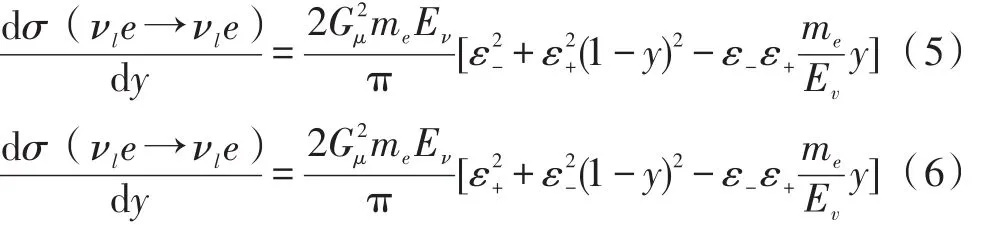
若不考虑影响，总散射截面为

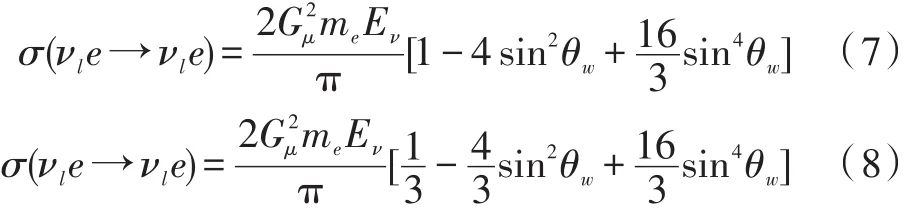
只是sin2θw存在有大约±3.5%的不确定度。

3）两者混合参与过程

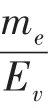
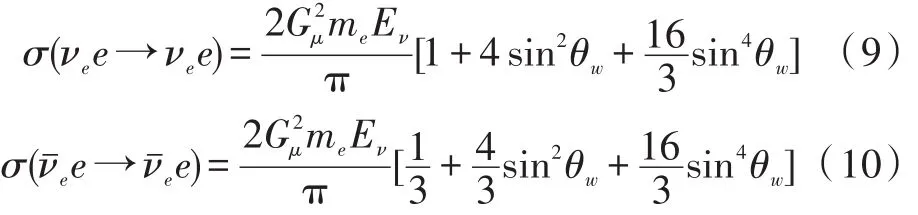
表1　散射过程界面的相对值

若要进一步对中微子散射进行弱电辐射修正，则需考虑包括单圈弱电辐射及光子韧致辐射修正。一般采用正则化修正最小差值，重新定义混合角，并将中微子散射界面测量精度差值控制在±0.1%，甚至更小的范围内。这也是新物理探针对νe散射测量的最低精度量级[10-12]。

1.2　标准模型外的散射效应

表2　我国对νee及散射界面测量统计数据

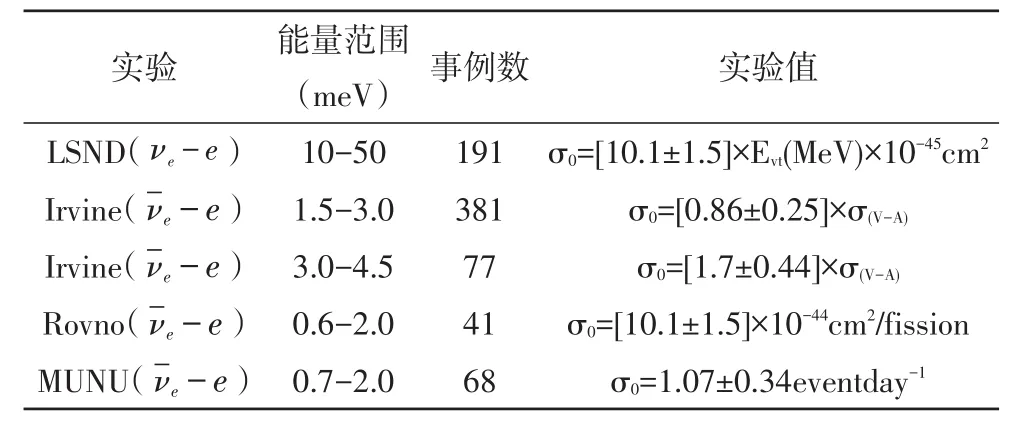
表2　我国对νee及散射界面测量统计数据

实验 能量范围（meV） 事例数 实验值LSND（νe-e）Irvine（-νe-e）Irvine（-νe-e）Rovno（-νe-e）MUNU（-νe-e）10-501.5-3.03.0-4.50.6-2.00.7-2.0191381774168 σ0=[10.1±1.5]×Evt（MeV）×10-45cm2σ0=[0.86±0.25]×σ（V-A）σ0=[1.7±0.44]×σ（V-A）σ0=[10.1±1.5]×10-44cm2/fission σ0=1.07±0.34eventday-1

研究统计表明，中微子散射过程影响参数有12个，主要影响参量有6个。由于散射过程影响参量复杂，且散射对不同参量敏感度不同。经过大量的分类观测统计，表3显示了自由度数以及其的比率关系[13]。数据结果表明，绝大多数NSI参数接近限制精度，比率也接近于1。这一结论对于进一步提高测量精度有着重要的推动作用。

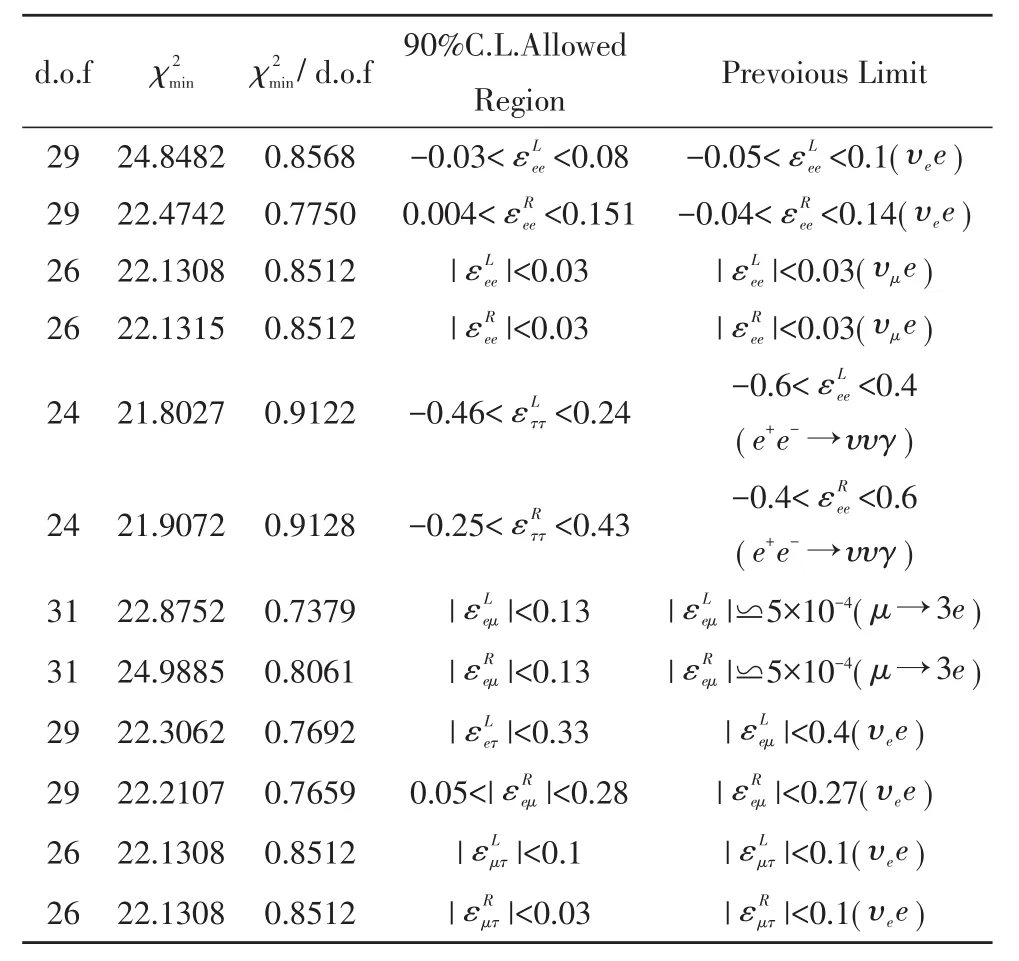
表3　各参量νee过程NSI参数的限制精度统计

2　小Higgs模型的重要扩展

SM模型虽然存在理论缺陷，但在低能状态下，其群结构依旧有效。引入小Higgs理论是为了将玻色子作为更高能标，以抵消SM中玻色子规范与顶夸克对粒子质量的二次修正，从而解决SM遗留的质量等级问题。小Higgs模型可看做在中微子质量理论基础上的扩展模型，又根据理论结构差异细分为直积群模型（LH）和简单群模型（SLH）[14]。

本文根据玻色子的自发性对称破缺，参考LH模型及费曼规则[2-4]，给出f的量级质量

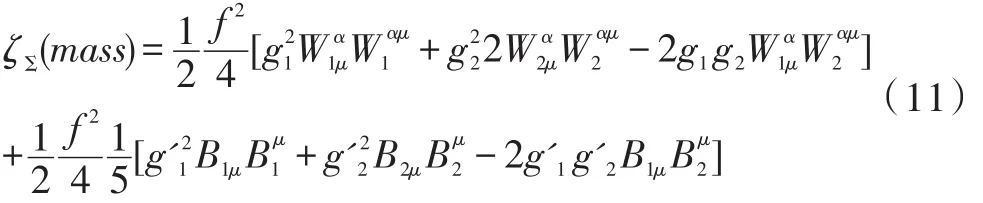
混合角为

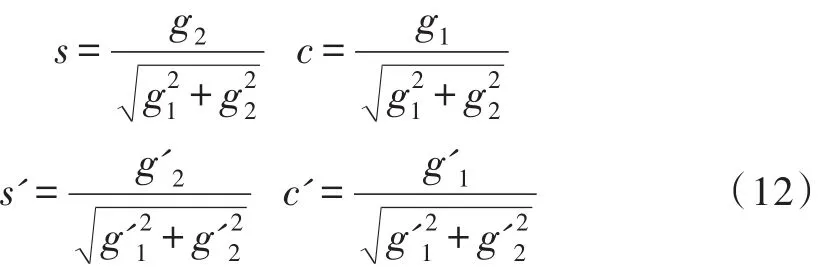
而SU（3）简单群模型的费米部分稍显复杂，共提出了两种不同的方式。在此不做赘述，可参考SLH模型作用和费曼规则[2-5]。

2.1　LH模型下νee→νee过程

LH模型下与SM标准模型相比，需要更多考虑耦合修正和新物理模型下玻色子质量的影响。因此，文中对散射截面引入修正项忽略小量级项，得到散射截面LH模型下表达式如下

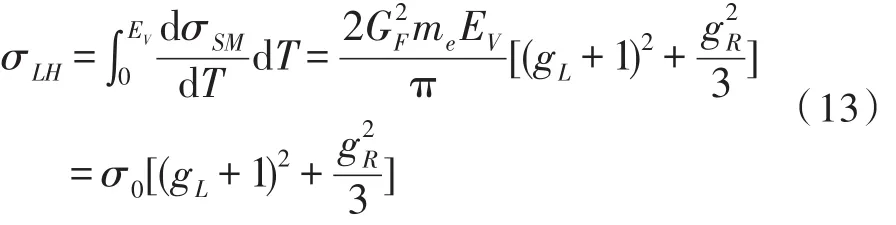
据此，本文通过LSND中微子实验进行了多次散射截面测试。采集大数据得到不同能标下的混合参数c与c'范围，如图1、2所示。由统计结果可知，当能标f提高至1.5TeV时，发现c'范围明显增大。阴影部分表示允许的LSND测量值。从图中可以看出，自由参数f、c与c'有着严格限制。根据目前国际规范玻色子的参数精确测量阈值为：1TeV≤f≤2TeV时，0.14≤c≤0.66，0.66≤c'≤0.8。其与本文测量的范围一致。

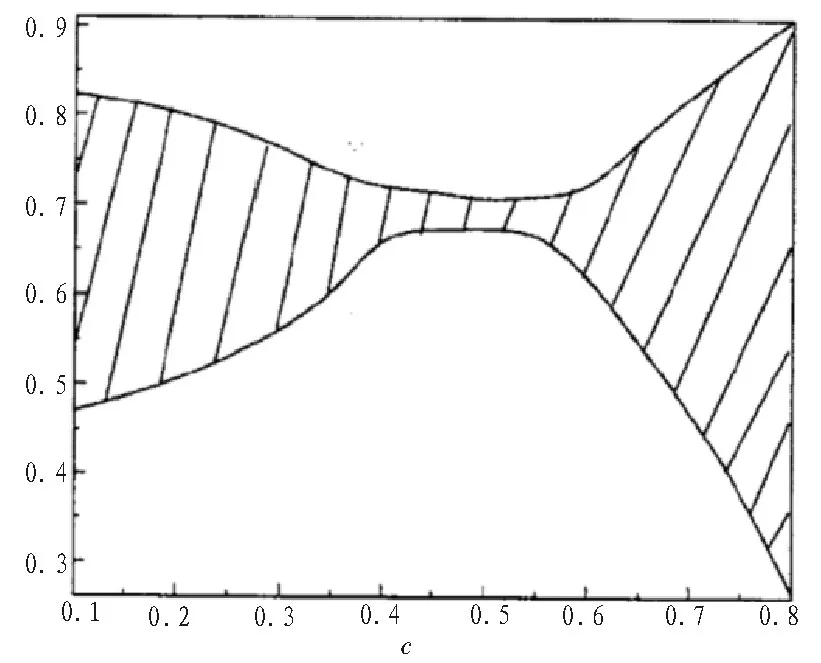
图1　能标为f=1TeV时，混合参数的取值范围

2.2　SLH模型下νee→νee过程

SLH模型下散射过程特征与LH模型类似，仍是考虑耦合修正引入修正项，忽略小量级，得到SLH自由参数tanβ与f的关系，如图3所示。由于SLH模型主要散射贡献就来自于tanβ与f，故可以通过曲线观察出，对应能标的为500GeV，1TeV和1.5TeV时，tanβ值大于2.9，1.6，1.1，同样符合电弱理论精确测量值范围[15-16]。

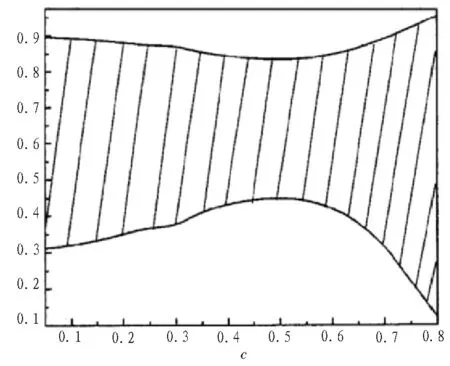
图2　能标为f=1.5TeV时，混合参数的取值范围

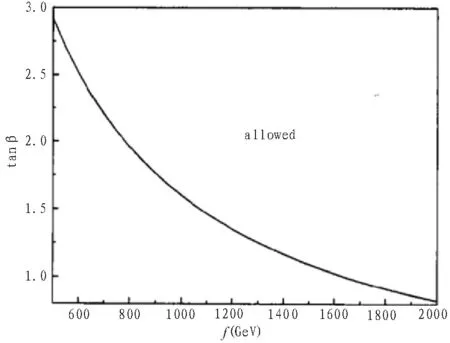
图3　SLH模型下tanβ与能标f关系曲线

3　结束语

基于现有新物理现象问题，文中需要对SM标准粒子模型进行扩展，但现有物理模型对于νee→νee过程的分析研究者较少。本文介绍了标准模型下的散射界面计算公式与影响参数，讨论了标准模型外的差异性。并根据现今国内外中微子实验，分析了主要的几种影响参数，以及其对νee的进度限制作用。尤其是基于小Higgs模型下的LH与SLH模型的散射参数修正，对于文中深入理解中微子、电子的粒子特性有着积极的作用。本文通过大量实验，得出了两种模型的参数限制区间与参量关系。并与LSND精确测量值范围对比，验证了文中模型的测量正确性和精确性。这一结论为未来研究高能粒子碰撞机理及中微子、电子的质量问题，提供了重要的理论依据与实验导向。

参考文献：