基于HHT和PCA的滚动轴承故障状态识别方法研究

俞 啸，董 飞，高 彬，张 立

（1.徐州医科大学医学信息学院，江苏徐州221009；2.中国矿业大学物联网（感知矿山）研究中心，江苏徐州221008；3.中国矿业大学信息与控制工程学院，江苏徐州221008）

滚动轴承的是旋转机械设备的重要组成部分，其健康状态将直接影响设备的安全运转。现有轴承故障识别研究中多采用振动信号的时域、频域和时频域的统计特性作为故障的特征信息[1-2]，例如平均值、标准差、峰度、偏度等。常用的振动信号时频分析方法有：小波变换[3]、短时傅里叶换[2]、魏格纳-维尔分布（Wigner-Ville Distribution，WVD）[4]，希尔伯特黄变换（Hilbert-Huang Transform，HHT）[5-7]等。Ali等[8]利用信号IMF分量的时域特征实现滚动轴承状态识别；Xue[9]等分别提取轴承振动信号的排列熵等特征作为识别系统的特征向量；Zhang等[10]利用时频域统计特征来训练SVM来提高滚动轴承的故障识别率；Bafroui等[3]提取振动信号小波系数中故障敏感特征。上述研究中的故障诊断模型都是基于统计特征的，然而，统计特征中只能包含振动信号中部分故障相关的特征信息，无法对故障特征进行完整的描述，可能导致故障识别准确率的下降[11]。

文中利用HHT边际谱（Hilbert Marginal Spect⁃mm，HMS）作为轴承故障状态的初步特征，引入PCA方法[12-13]，提取HMS的主成分信息，利用HMS主成分作为为特征向量，实现对轴承故障模式分类器的训练，建立HHT-PCA-SVM模型，实现轴承故障模式识别，实验结果表明PCA可以从HMS中提取出目标更加敏感的低维特征信息，从而提高类轴承故障的识别率。

1　HHT和PCA分析

1.1　HHT边际谱

Empirical Mode Decomposition（EMD）可以将x（t）信号分解为不同尺度的本征模态分量（Intrinsic Mode Function，IMF），如公式（1）

对ci（t）进行 Hilbert变换：

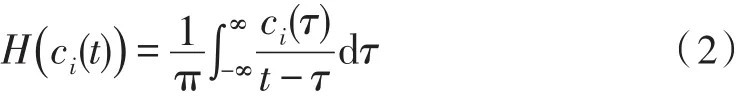
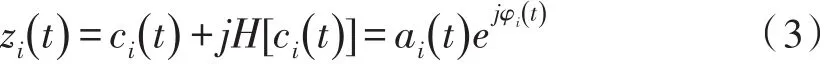
计算幅值函数和相位函数：

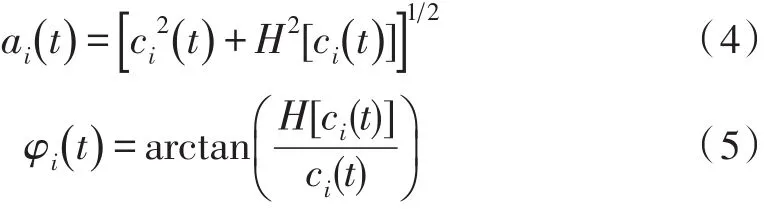
得到瞬时频率:

x（t）的 Hilbert谱表示为：

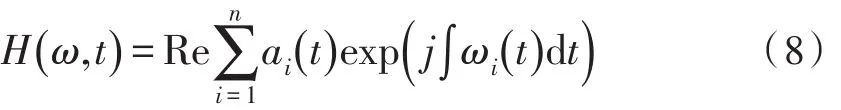
边际谱h（w）表示为H（w,t）的时间积分：

边际谱h（w）代表信号的幅值在整个频率段上随频率的变化的情况[5]。

1.2　主成分分析（PCA）

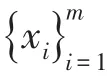
可以由式（11）将xi变换为：

其中：U是一个n×n正交矩阵，ui是样本C（协方差矩阵）的第i个本征矢量。

PCA求解过程转换为本征矢量求解过程：

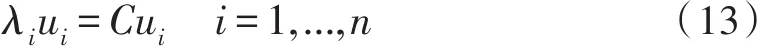
其中λi是C的一个本征值，ui是相应的本征矢量。

2　HHT-PCA-SVM故障诊断模型设计

HMS能够表征信号瞬时频率特征，同时也存在大量的冗余信息。这里采用PCA对HMS进行降维处理，实现对HMS的二次特征提取，取前p维的主成分分量建立故障主成分特征向量，利用主成分特征向量对SVM分类器进行训练[16]，建立HHT-PCASVM故障分类模型。结合交叉检验方法和粒子群优化算法（Particle Swarm Optimization，PSO）对模型SVM惩罚因子c，核函数参数g和p参数进行优化，模型工作过程如图1所示。

3　实验分析

3.1　实验数据介绍

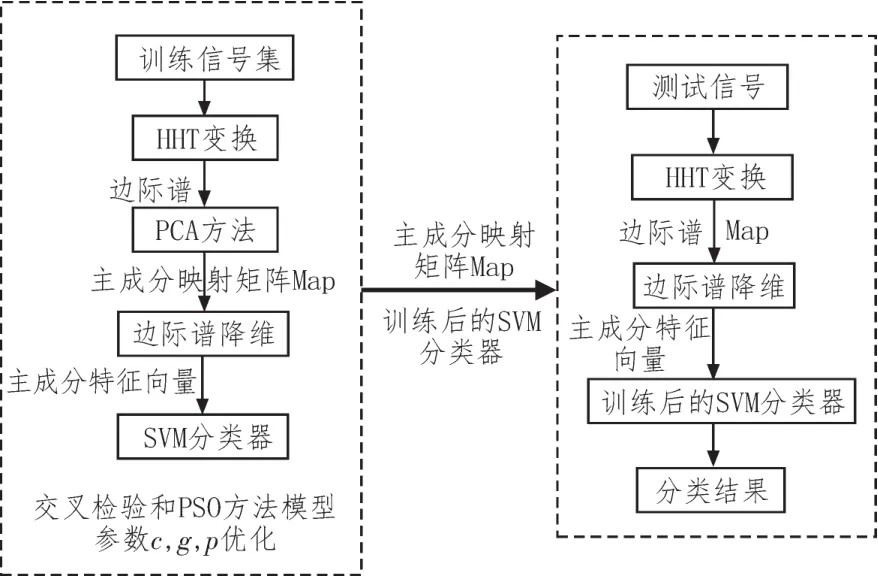
图1　HHT-PCA-SVM分类模型

利用凯斯西储大学的轴承故障实验台振动数据[16]开展实验研究，轴承试验台装置如图2所示，由一个2HP的三相感应电动机（左侧）轴和一个用于产生额定负载的测力计（右侧）组成，实验台驱动端和风扇端各有SKF-6205-2RS轴承一个，分别对振动传感器采集的两端（Driver-D，Fan-D）振动信号进行分析，完成对表1所示的10种轴承状态振动信号的识别，每个样本为2000个采样点构成的信号，10种故障信号各取60个样本，共600个样本，随机抽取每种信号20个样本作为训练集，剩余40个样本作为测试集，完成对HHT-PCA-SVM模型的训练和测试。

图2　CWRU轴承故障试验台

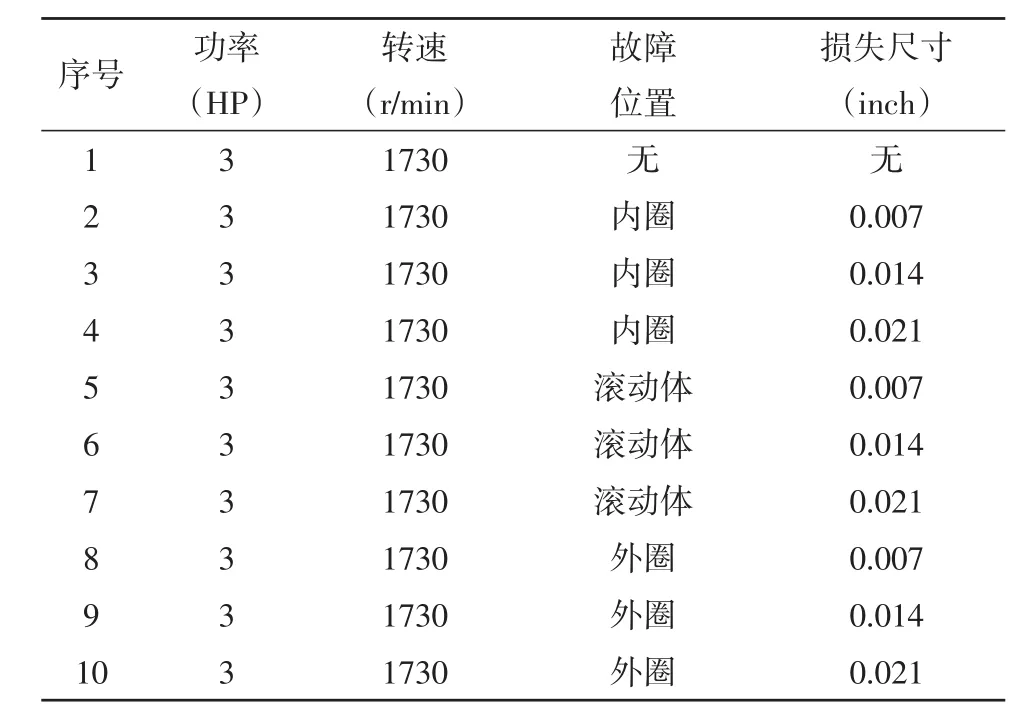
表1　实验选取的驱动端轴承故障种类

3.2　振动信号HHT分析

首先对训练数据集振动信号进行EMD分解，得到信号的各阶IMF分量，然后对IMF分量进行Hilbert变换，求信号的HMS。计算前三阶IMF分量的希尔伯特包络谱，如图3（b）～（d），在转频、故障频率点及其两倍频附近（29.3 Hz，105.5 Hz，205.1 Hz）处出现明显谱线，同时存在若干干扰谱线，图3（e）为外圈故障的HMS。

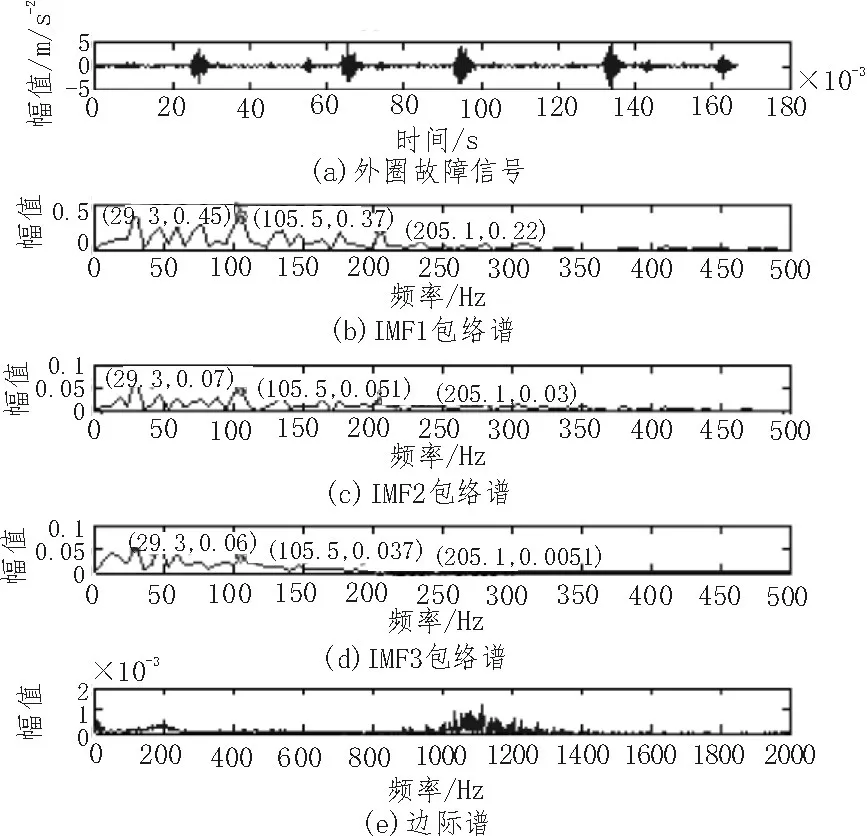
图3　轴承故障振动信号HHT分析

3.3　PCA降维效果分析

利用PCA对HMS进行降维处理，降维后选取的特征维数为p，在c和g取定值的条件下（c=8，g=1），p值和HHT-PCA-SVM模型故障种类识别准确率之间的关系如图4所示，当p值较小时，选择的主分量少，特征信息不足，模型识别准确率不高，随着主成分维数的增加，模型识别率迅速准确提高，并在10～25之间达到峰值。

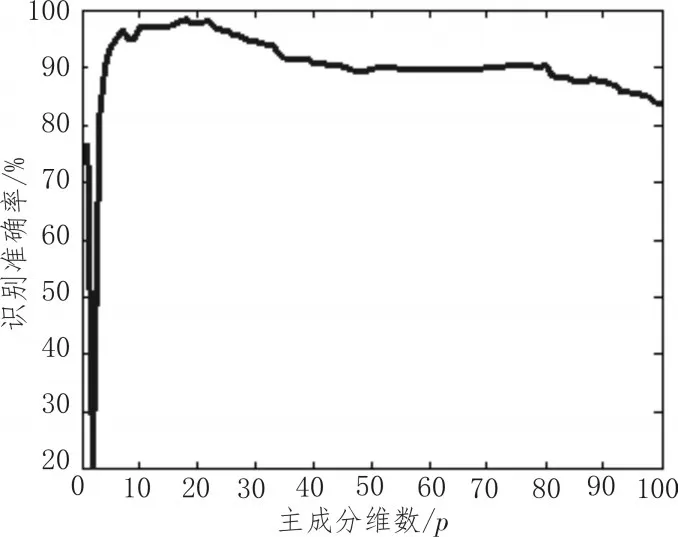
图4　识别准确率和主成分维数之间的关系

3.4　对比实验结果分析

为了验证特征提取方法的有效性，分别采用时域和频域统计参数和SVM结合的ST-SVM模型、统计参数和PCA结合的ST-PCA-SVM模型，HHT边际谱和SVM结合的HHT-SVM模型，以及HHT-PCASVM模型对驱动端Driver-D和风扇端FAN-D轴承故障数据集实验分析。

ST-SVM中，对振动信号进行EMD分解，提取前4阶IMF分量及其希尔伯特包络谱的统计参数构成特征向量，训练SVM分类器。这里选取每个IMF分量的5种时域参数和5种频域参数，具体参数见表2。在ST-PCA-SVM中，对ST-SVM进行PCA分析，提取主成分分量构成特征向量，训练SVM分类器。

表2　时域和频域统计特征参数

包络谱sp（k）的能量可以表示为：

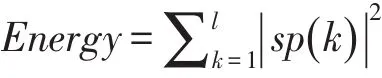
sp（k）的能量熵定义为 ：

其中，

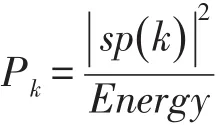
sp（k）的能量熵能够反映IMF分量在频域上的能量分布不确定度，不同故障状态振动信号的能量熵值存在差异，常作为统计特性来表征故障位置和故障程度。

结合交叉验证和PSO优化方法，对模型的最佳参数进行寻优，得到优化模型，各模型的分类效果如表3所示。

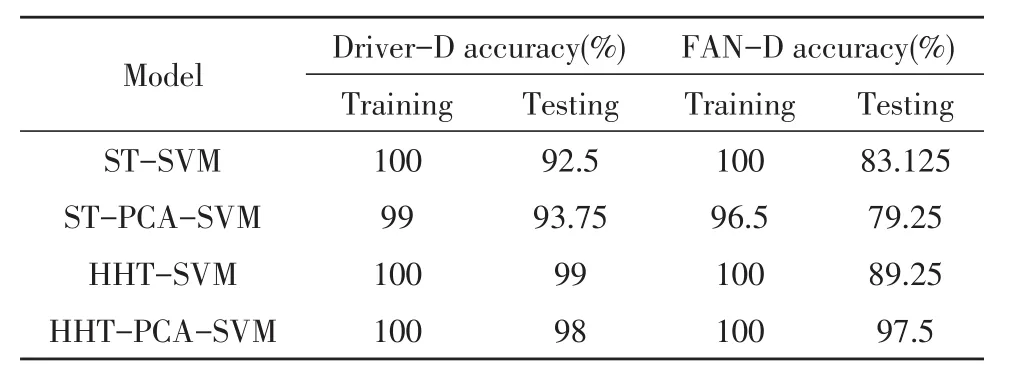
表3　各故障分类模型的分类结果

根据表3的结果可以发现，对于驱动端轴承数据集Driver-D，基于统计特性的ST-SVM和STPCA-SVM模型性能一般，而基于HMS的HHT-SVM和HHT-PCA-SVM模型可以取得较高的识别准确率。而对于风扇端轴承数据集Fan-D，ST-SVM和ST-PCA-SVM及HHT-SVM模型性能相比于数据集Driver-D均出现大幅度下降。这是由于风扇端轴承距离传感器较远，从振动信号中提取的信息中存在更多与故障状态相关度低或不相关的信息，PCA方法可以从HMS中提取出目标性更强的高层特征抽象，所以HHT-PCA-SVM模型依然可以保持较高的识别准确率。

4　结 论

针对滚动轴承故障状态识别问题，将振动信号的HMS作为初步特征，利用PCA算法提取出HMS中的故障状态敏感信息，以提取出的主成分特征向量作为输入训练分类器，利用HHT和PCA完成特征构建，结合SVM方法提出了HHT-PCA-SVM轴承故障识别方法。利用美国凯斯西储大学的轴承故障实验台开放振动数据对HHT-PCA-SVM进行实验分析和验证，针对驱动端和风扇端轴承分别选取10种不同位置、不同程度的故障信息进行分析。通过实验验证的方式分析模型参数p，g和c对识别准确率的影响，实验结果表明，选择合适的模型参数可以提高模型的识别准确率。对于测试集数据，HHT-SPARSESVM模型驱动端轴承故障状态识别率为98%，风扇端轴承故障状态识别率为97.5%，相比于ST-SVM和ST-PCA-SVM及HHT-SVM模型，HHT-SPARSESVM模型可以得到较高的故障识别率，并具有较强的适应能力。