基于海浪修正的海上无线电波传输模型

2018-06-11殷昊天胡浩博田乐琪李子钰

数字通信世界 2018年5期

殷昊天，胡浩博，田乐琪，李子钰*

（1.吉林大学数学学院，长春 100032；2.中山大学数学学院，广州 510275）

1 引言

短波通信或称高频通信（HF）是指在3-30MHz频段范围内，通过电离层反射进行远距离或通过地波进行近距离传输的一种通信手段。在大约100公里到数千公里范围内，不需要中继站就可以超视距通信。本文建立短波无线信号在海洋传播中功率变化的模型，计算不同功率电波在海洋传播中在电离层与海平面间反射来回的跳数，用来计算其在海洋上传播的最远距离，希望为找寻适合不同环境的最佳无线通信技术方案，设计通信系统，减少工程设计的盲目性打下基础。

2 无线电波在电离层和海面跳跃传播模型的建立

海洋无线电波发射后，会在电离层与海平面之间不断反射，直到其功率下降到其信噪比低于可用信噪比时，无线电波消散于空中（图1）。当其频率高于最大可用频率（MUF）时，无线电波将穿越电离层。无线电波的功率在传播中有三种改变机制，即空气传播损耗，电离层反射的损耗，以及海平面反射的增强效应。其中空气中的损耗与其在空气中的传播距离、无线电波频率相关；电离层反射的损耗与电离层的反射系数相关；海平面的反射与无线电波进入海洋的入射角、海平面波涛汹涌的程度有关。

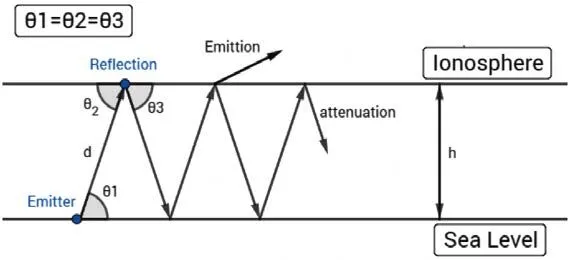
图1 无线电波在电离层与海面间的跳跃传播过程示意图

无线电波在电离层和海平面间传播时，其功率变化的计算如图2所示：P表示无线电波的功率；P（d）表示在空气中传播距离为d时功率的损耗；T1为电离层的反射率；T2为海面的反射率。

2.1 在空气中传播距离为d时无线电波功率损耗P（d）的计算

依照自由空间中无线电波功率损耗公式：

式中，d表示传播距离（km）；k为路径损耗因子；一般在2-5之间；f为无线电波的频率（Hz）。

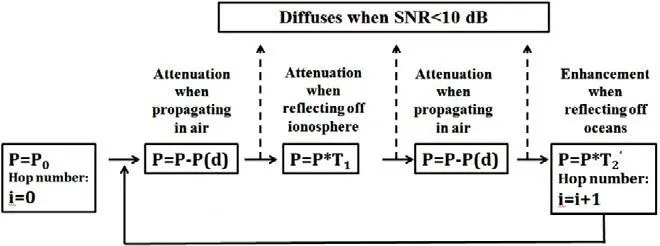
图2 无线电波在电离层和海面间传播时，功率变化的计算

2.2 电离层反射时功率的损耗

电离层主要是由太阳的紫外辐射引起的，故电离层电子密度随太阳辐射的强弱变化具有明显的昼夜、季节、年、太阳黑子周期等变化规律，并且总是随纬、经度呈现复杂的空间变化。

Guru和Hiziriglu分析了1937年到1952年间，电离层对4Hz无线电波反射率随太阳黑子变化的变化情况，发现其基本在-ln2.5附近波动（4）。我们取电离层对无线电波的反射率为-ln2.5。即T1=e^-2.5。

2.3 海面反射时功率的变化

2.3.1 平静海面的反射率T2的计算

海水非磁性，所以只要考虑它的介电常数。用菲涅尔公式可以来描述无线电波反射时入射角与反射介质介电常数对无线电波电场强度的影响。

在本模型中，反射介质为海水，ε为海水的相对介电常数，θ为无线电波入射角。ω是反射前后短波的电场强度之比。由麦克斯韦方程组可解出无线电波功率之比为电场强度之比的平方，故反射前后的功率之比，即海平面反射率T2=|ω|2。值得注意的是，算出的ω可能为负数，这是其辐角有相位的物理含义决定的，并不影对反射系数的求解。

2.3.2 波涛汹涌海面的反射率T2’的计算

国际上通用道格拉斯海情表中波浪的高度来描述海面波涛汹涌的程度。在有波浪的情况下，用修正因子ρ来计算反射率，国际无线电委员会（CCIR）给出了ρ的表达式：

2.4 无线电波在电离层与海平面间反射跳数的计算

无线电波的功率在空气中变化，及其在电离层和海平面间跳数的计算，如图2所示。无线电波发射到空中时，会依次经历空气传播、电离层反射、空气传播以及海面反射，依次重复。当以上四个步骤被完成一轮后，经历一个海平面与电离层间的反射来回，即跳数增加1，直到其信噪比低于最低信噪比（一般为10 dB），无线电波消散于空中，算法终止。计算其消散时的最大跳数，即在电离层与海平面间反射的跳数。

2.5 无线电波在海洋中有效传播距离的计算方法

要计算无线电波的传播距离，只需计算无线电波每一跳传播的距离，再与跳数相乘。图4为跳数为1时的无线电波传播示意图。无线电波从E点以发射角β发射（入射角θ=90°-β），至电离层I处反射后到达G点，被轮船接受。图中无线电波的传播距离为弧EG的长度（公式：弧EG=2*α*Re），K点为地心，Re为地球半径（取6371 km），H为电离层F2层高度（取210 km）。α为发射点K与反射点I与地心K连线的夹角。

通过几何计算，我们可得角α的计算公式：

3 仿真分析

3.1 波浪修正系数ρ的仿真分析

由修正系数ρ的计算公式（3）可知，它受频率f、入射角θ及均方根波高h的影响。由于短波通讯中无线电波的频率一般是固定的，我们在此取频率f为4Hz，分别考虑入射角θ、均方根波高h对波浪修正系数ρ的影响。

我们将均方根波高固定在4m、9m、12m（分别对应道格拉斯海情表中的几个关键的海浪强度分界线），分别计算修正系数ρ与入射角θ的关系（图5）。

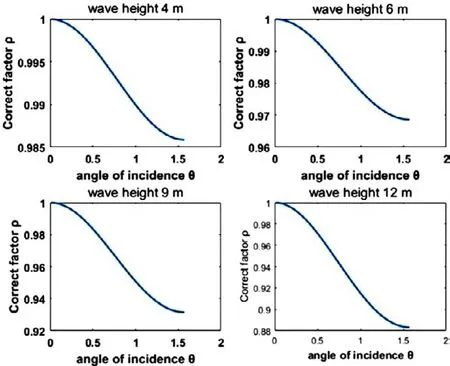
图5 波浪均方根波高固定时，修正系数ρ与入射角θ的关系

由图5我们可以看出，在不同的均方根波高下，波浪修正系数ρ随入射角θ的变化趋势基本一致。随着入射角度θ的增加，ρ不断下降，在入射角为45°时，其下降的速率达到最大。θ=0时是垂直入射，修正系数为1，此时平静海面与波涛海面没有差异。之后随着θ变大，修正系数越来越小，平静海面与波涛海面的差也越来越大。

将θ固定在30°、60°时，计算均方根波高h对波浪修正系数ρ的影响。结果如图6。由图可以看出，在不同入射角度θ情况下，修正系数ρ随均方根波高h的变化趋势基本相同，且随着均方根波高的增加，修正系数不断下降，即影响越大。当均方根波高比较小时（不超过4），ρ接近1，这与平静海面无需修正这一基本事实相符。当均方根波高较大时，ρ的值就急剧减小。

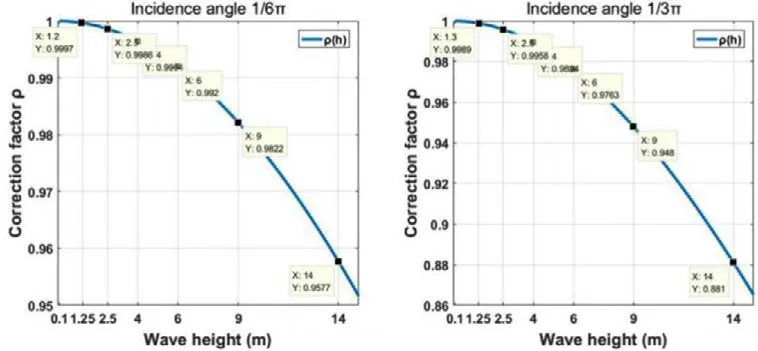
图6 入射角θ固定时，修正系数ρ与波浪均方根波高h的关系

3.2 无线电波在电离层与海平面间反射跳数的仿真计算

目前，国际航行船舶船载短波通信发射设备发射功率多为150W和250W，我国天津、上海和广州3个海岸电台发射设备功率多为5 kW和10 kW （5）。我们根据实际情况与文献资料，取电离层反射率，均方根波高取4米，路径损耗因子k取3.5，发射频率f取 4 Hz。通过模型算法使用MATLAB软件编写程序，得到不同发射功率下无线电波在电离层和海面间反射的跳数。

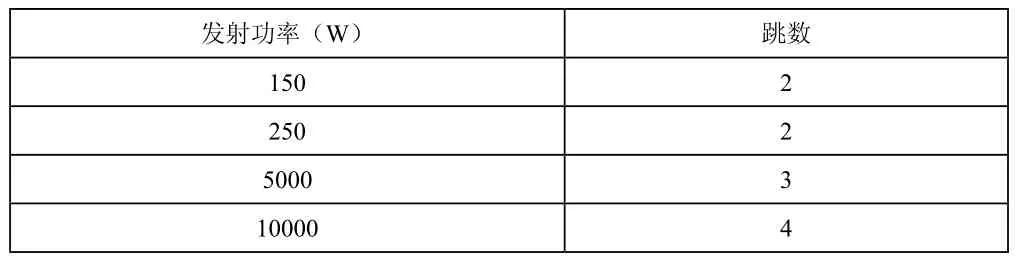
表1 不同发射功率时无线电波在电离层和海面间的反射跳数

我们曾尝试计算反射跳数与发射角度的关系，发现发射角度对跳数几乎无影响。

3.3 无线电波在海洋中有效传播距离

波涛是4米的时候，传播距离与发射角的关系曲线如图7。

150 W和250W功率的无线电波，如果沿着地平线发射出去，即发射角是0，将会得到最远传播距离6194 km。而5 kW或10 kW功率的无线电波，发射角是0时，最大传播距离可以达到最大9291 km的传播距离。如果垂直发射出去，即发射角是传播距离为零。另外，由图像也可以看出来附近是一个显著的拐点，高于时最大传播距离变化较缓慢，值较低，属于比较近的传播距离。因此在实际应用中，射角都不会超过