城市轨道交通地下线路有砟轨道应用的可行性分析

■ 王雅群 彭华 陈军华

2008年以来，我国进入城市轨道交通建设“大繁荣”时期。在我国新建城市轨道交通线路中，绝大多数采用无砟轨道。但是，相较于有砟轨道，无砟轨道具有以下缺点：

（1）造价高，初期投资大；

（2）几何状态调整仅靠扣件实现，变形较大时调整困难且代价巨大；

（3）使用中易出现波磨现象，导致振动明显、噪声增大，严重影响乘客舒适度，增加养护维修费用。

无砟轨道的缺点在一定程度上制约了城市轨道交通的发展，而在巴黎、伦敦、柏林、赫尔辛基等国外城市的城市轨道交通地下线路正线中，20世纪初期铺设的有砟轨道仍在正常使用，总结并参考国外城市轨道交通地下线路有砟轨道应用的成功经验十分必要。鉴于此，在分析国内外有砟轨道在城市轨道交通线路中应用现状的基础上，从经济评价、环境评价、结构动力特性、铺设条件及养护维修等方面对有砟轨道在城市轨道交通地下线路中应用的可行性进行探讨和研究。

1 经济评价

根据国内外轨道交通建设经验可知，无砟轨道初期投资大约为有砟轨道的1．5倍，如日本板式无砟轨道与有砟轨道的初期投资比例为1．3～1．5，德国R h e d a型无砟轨道与有砟轨道的初期投资比例为1．5～1．7[1-2]。根据我国情况：钢弹簧浮置板道床为1 700万元/km，梯形轨枕道床为1 200万元/km，弹性长枕道床为650万元/km，碎石道床为530万元/km。无砟轨道与有砟轨道建设及维修费用对比见表1。

无砟轨道初期投资和经济效益问题十分复杂，影响因素也较多。由表1可知，在建设及维修费用方面，无砟轨道明显高于有砟轨道。由于无砟轨道对养护措施水平要求较高，为保障无砟轨道的质量，在施工工序和质量控制等方面会花费较多的额外费用和时间。此外，对于桥梁和路基上的无砟轨道，因控制基础长期沉降而需增加的费用为有砟轨道的2．0～2．5倍。如今，有砟轨道结构维修技术较成熟，在很大程度上实现了机械化和自动化，大型养路机械作业的精度和质量大幅提升，轨道几何状态保持得以延长，其费用低于手工作业；若考虑无砟轨道达到寿命周期后高昂的再建费用，有砟轨道的经济效益更为明显。

表1 无砟轨道与有砟轨道建设及维修费用对比

2 环境评价

2.1 噪声评价

列车噪声限值采用A加权等效声级[3]，对于列车运行时速30～90 km的轨旁噪声，支承块式无砟轨道比有砟轨道大2．8～4．5 dB（A）。

对北京1、2、4（含大兴线）、5、13号地铁部分线路进行车内噪声测量：1、2号线噪声暴露水平Leq约为76 dB（A）；4、5号线噪声暴露水平Leq约为80 dB（A）；13号线噪声暴露水平Leq约为70 dB（A）。北京地铁1、2、4、5号线几乎全线采用无砟轨道；13号线主要为地面线，几乎全线采用有砟轨道。分析可知，有砟轨道振动噪声暴露水平Leq比无砟轨道小6～9 dB（A），有砟轨道线路降噪效果优于无砟轨道。

2.2 振动评价

选取振动加速度级及其对应的振动级对振动强度进行描述和评价，是目前国际上广泛采用的方式。假设某点在某一方向的振动加速度的有效值为a，可得其对应的振动级 L[4]：

式中：L为振动加速度有效值对应振动级，dB；a为经振动感觉校正的振动加速度有效值，m/s2；a0为振动加速度基准值，一般取1×10-6m/s2。

相对垂直或水平振动，可按给定频率响应曲线计算a：

式中：n为频率，Hz；an为频率分量的振动加速度有效值，m/s2；Cn为频率的相对响应，dB。

通过计算，可得不同轨道结构形式的轨道结构振动加速度级（见表2）。由表2可知，与普通钢筋混凝土整体道床相比，碎石道床更大幅减少了轨道振动向隧道的传播，其振动加速度级的减小量为8～10 dB。对于整体道床而言，梯形轨枕、弹性短轨枕、轨道减振器等轨道减振措施对低频振动的减振效果一般劣于高频（50 Hz以上）减振效果，而有砟道床的减振频域更广阔，且对中低频的振动也有较好的减振效果。采取在道床底部铺设弹性垫层或在轨枕底面设置弹性垫层等减振措施后，有砟轨道的减振效果明显提高，道砟捣固周期及有砟道床使用期限进一步延长。

3 地铁隧道内有砟轨道铺设条件

有砟轨道与无砟轨道的道床断面尺寸等结构参数不同，因此在设计新建城市轨道交通地下线路中的有砟轨道时，为满足运营安全，隧道断面会有相应变化。隧道内采用有砟轨道的线路形式，轨道结构高度比无砟轨道高10～20 cm，所以隧道断面净高需进一步增加，地铁车辆的建筑限界也需进行修改。结合对隧道内有砟轨道道床断面的分析可知，如在直径6 m的盾构隧道内使用有砟轨道，将不能满足地铁设计相关规范及车辆限界的要求。因此，建议增加盾构隧道直径，内径由5．4 m增至5．8 m或以上，以满足盾构隧道中使用有砟轨道的限界要求。此外，隧道内道床排水可采用线路两侧或单侧的方式，考虑到有砟轨道的使用年限及维修周期，建议采用线路两侧排水的方式。

综合地铁车辆类型、列车的设计运营速度及施工难易程度，特别考虑道床相关力学性能、线路稳定性等方面的因素，当列车运行时速大于80 km且正线半径较小时（A型车小于500 m，B型车小于450 m），建议使用宽轨枕，或采用道砟胶的方式来提高线路稳定性，以保证安全运营。对于有砟轨道曲线地段，应采用适当的线路超高、隧道限界及道砟堆高，以满足列车运行要求。此外，轨道基础沉降问题一直困扰着城市轨道交通，当采用无砟轨道时，为控制基础的长期沉降，需增加较多的后期养护维修费用，而采用有砟轨道可以通过道砟补充较为容易地克服沉降问题，且有砟轨道的养护维修可实现机械化和自动化，养护维修费用较低。

表2 不同轨道结构形式的振动加速度级 dB

4 有砟轨道结构动力特性分析

4.1 动力分析模型

采用ABAQUS有限元分析软件进行建模计算时，基于耦合动力学理论[5]，根据结构形式、悬挂特性等对城市轨道列车进行模型化处理。将列车车体、2个转向架及4个轮对视为刚体，列车模型就成为1个多刚体系统，该系统视为由1个车体、2个转向架及4个轮对组成，彼此间以两系弹簧阻尼器元件进行连接。在“列车-轨道”空间耦合动力分析模型中，车体和转向架各有沉浮、点头、横移、侧滚和摇头5个自由度；轮对则具有沉浮、横移、侧滚和摇头4个自由度，不考虑车轮转速不均匀产生的回转[6]。“列车-轨道结构-隧道”耦合动力学模型见图1。

4.2 主要计算参数

城市轨道交通隧道内有砟轨道包含道床、轨枕、扣件、钢轨等结构，模型建立时，对隧道结构进行适当简化，只考虑仰拱（采用C35混凝土）、拱墙（采用C35混凝土）、仰拱回填层（采用C20混凝土）、喷射混凝土层（采用C25混凝土）及衬砌外部的部分围岩。以修改钢轨模型节点坐标的方式，将不平顺样本分布施加于左、右钢轨。其中车体质量22．80 t，转向架质量2．50 t，轮对质量1．76 t。采用60 kg/m钢轨；扣件间距为0．625 m，扣件系统垂向动刚度取75 kN/mm，横向动刚度取40 kN/mm；

图1 “列车-轨道结构-隧道”耦合动力学模型

其他相关参数的设定参考相关规范与文献。

4.3 动力特性计算结果及分析

模型建立后进行计算，部分典型的仿真结果时程曲线见图2—图7，时程曲线取自列车时速60 km时系统的动力响应。

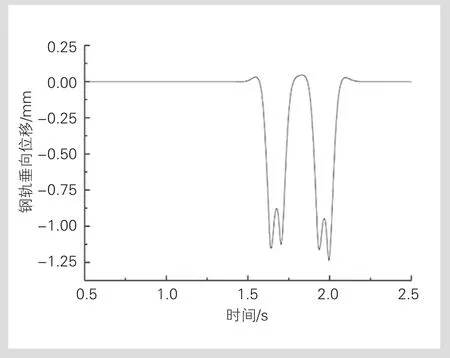
图2 钢轨垂向位移

图3 钢轨横向位移

图4 碎石道床垂向加速度

图5 隧道垂向加速度

图6 轮重减载率

通过建立“列车-轨道结构-隧道”耦合动力学模型并进行动力响应计算，可获取模型计算结果峰值（见表3）。由表3可知，隧道内有砟轨道的安全性指标、车体平稳性指标、轨道结构动力响应指标、振动指标等数据均小于限值要求，可知在城市轨道交通地下线中采用有砟轨道结构，无论在结构安全、动力响应等方面，还是在乘客舒适度及噪声振动方面都是可行的。

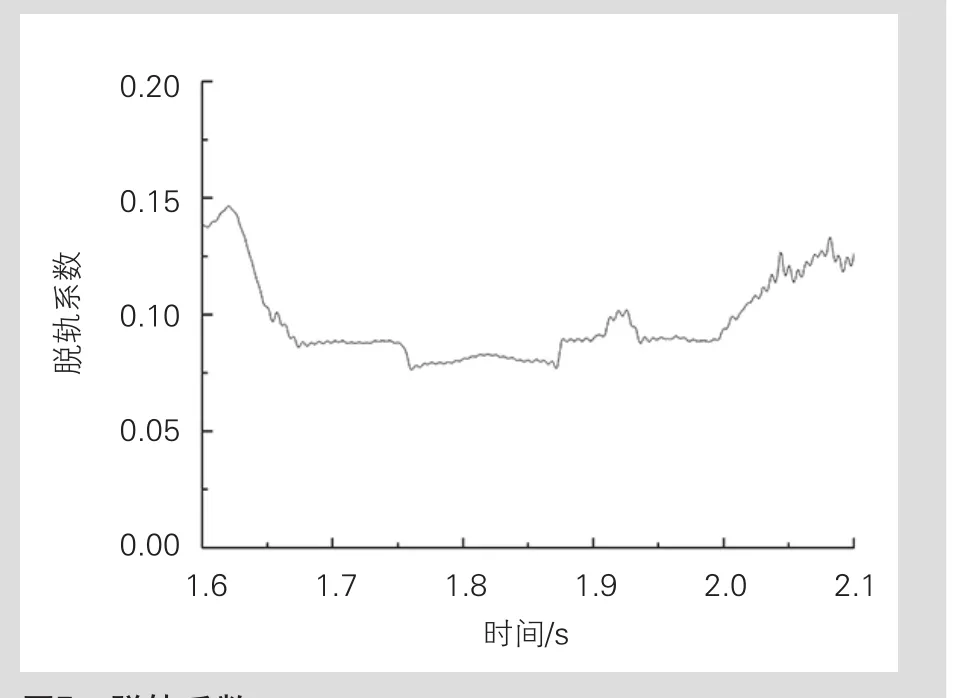
图7 脱轨系数

5 地铁有砟轨道养护维修

有砟轨道在养护维修方面作业时间短、效率高，对既有线路影响小，虽然维修工作量相比无砟轨道较大，但考虑地铁轴重较小，可通过道砟固化等方式有效减少维修量。

参照国内外高速铁路及普速铁路有砟轨道线路的建设及运维经验，在隧道内铺设有砟道床时，应将隧道二次衬砌下部光滑的混凝土断面拉毛或设置道砟槽，增大道砟与隧道底面间摩阻力，保证道床纵横向阻力，提高线路平顺性及安全性；按设计速度开通前，应使用大型设备进行捣固稳定；道床铺设结束后，在城市轨道交通运营初期，列车应采取阶梯提速方式，进一步稳定道床；运营后期，应使用小型机械对有砟道床进行养护维修。

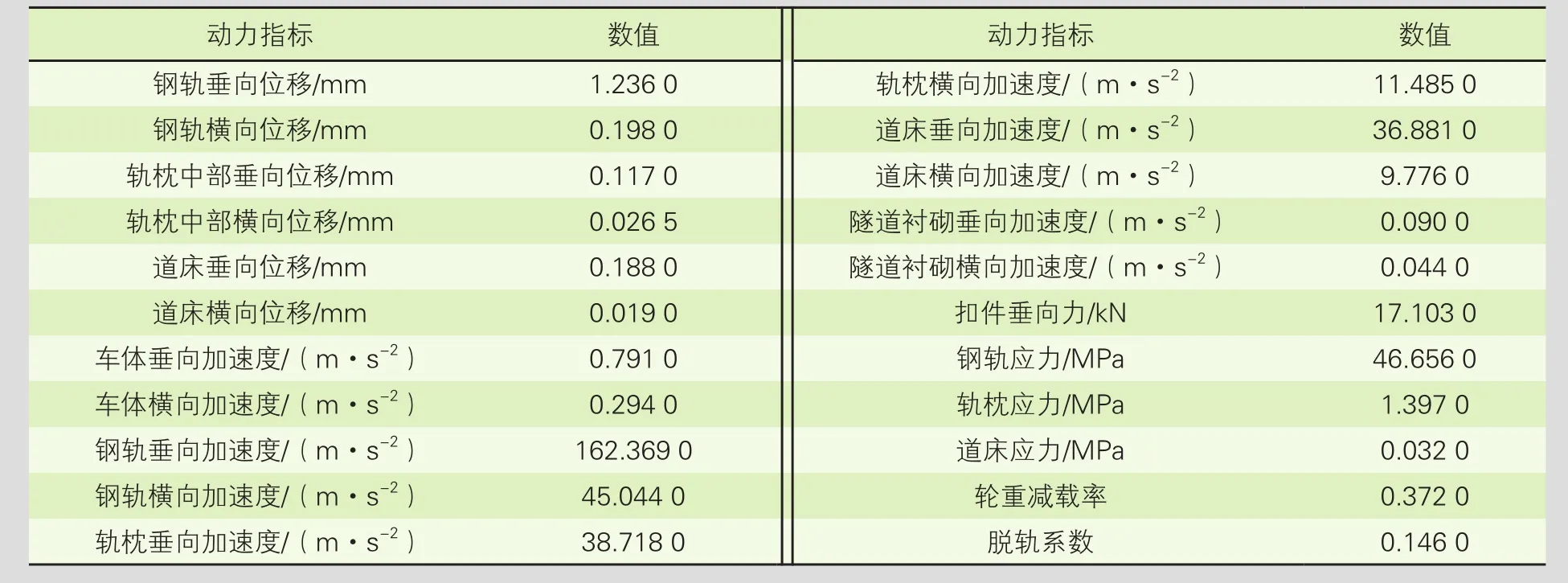
表3 隧道内有砟轨道的动力响应计算结果

为确保列车以规定速度安全、平稳且不间断运行，保持和提高线路设备的质量，最大限度延长各设备使用寿命，需对轨道在使用过程中产生的各种变形采取相应养护维修措施。因此，应合理划分、严谨组织相关维护工作，对其工作性质、内容、标准、要求及实施周期作出详细规定。为适应大型机械化、开天窗维修及大修队的现代化作业方法需要，在遵循“预防为主、防治结合、养修并重”技术原则基础上，在经常维护中应逐步实现养修分开。考虑地铁运量及道床脏污等病害，在保证每2年至少1次的大型捣固基础上，隧道内有砟轨道的线路大修周期宜定为20年。

6 结束语

综上所述，有砟轨道在经济效益、减振降噪及病害防治等方面相对于无砟轨道具有一定优势，在动力响应和养护维修等方面满足列车正常运营要求。因此，在城市轨道交通地下线路中铺设有砟轨道具有可行性。建议在新建城市轨道交通隧道中，选取典型试验段，从实践及技术储备的角度出发，进一步论证有砟轨道在城市轨道交通地下线路中应用的可行性。

[1] 李怀龙，李远富． 轨道交通无砟轨道经济评价研究综述[J]． 城市轨道交通研究，2015，18(2)：49-52．

[2] 朱晓兵． 轨道交通TOD模式落地的难点与推进路径[J]．铁路技术创新，2017(5)：15-18．

[3] GB 14892—2006 城市轨道交通列车噪声限值和测量方法[S]．

[4] 安胜利，杨黎明． 转子现场动平衡技术[M]． 北京：国防工业出版社，2007．

[5] 夏禾．车辆与结构动力相互作用[M]． 北京：科学出版社，2002．

[6] 辛涛，高亮，郑晓莉，等．车辆-有砟轨道-桥梁系统动力分析模型及验证[J]． 北京交通大学学报，2011，35(3)：72-76．