基于CVM的海涂湿地生态服务价值的模糊评估模型
2018-06-07王显金钟昌标
王显金,钟昌标
1 宁波大学商学院, 宁波 315211 2 宁波大红鹰学院, 宁波 315175
生态系统服务是指生态系统及生态过程所形成与维持的人类赖以生存的自然环境条件与效用[1]。正确评估海涂湿地生态服务价值有助于加强人们保护海涂湿地的意识,同时为海涂湿地围垦生态补偿标准的制定提供依据,对自然资源资产价值评估也具有重要借鉴意义[2]。海涂湿地生态服务价值评估方法一般有直接市场法、揭示偏好法和陈述偏好法等3种[3],陈述偏好法主要包含条件价值法(CVM)和选择实验法(CE)。
CVM是基于效用最大化原理,通过构建假想市场得到人们对非市场物品的支付意愿与补偿意愿,进而得到非市场物品的全部价值尤其是非使用价值的方法[4- 5]。CVM是以消费者效用恒定的福利经济学为基础,在Hicks提出的福利计量指标补偿变动与等价变动的理论基础上发展而来[6]。国内外对海涂湿地生态服务价值的研究一般基于Costanza 、De Groot或MA的生态系统服务分类体系,以直接市场法和揭示偏好法为主,根据不同方法评估研究区域相应的各类生态服务价值(能值)并逐项求和,其中文化服务和支持服务价值评估常采用CVM法[3,7-15]。国内外海涂湿地CVM研究主要从围涂工程导致海涂湿地生态服务价值损失或生态恢复成本角度进行评估,如Kim、Ndebele等从生态恢复角度分别评估了南朝鲜顺天等四处海涂湿地、新西兰霍克湾海涂湿地生态服务价值,赵斐斐、肖建红和么相姝等人分别对连云港海滨新城、南通市通州区滨海新区、天津七里海等区域生态服务价值损失进行了测算[16- 20]。在WTP/WTA计算方法选择上,一般对支付卡法、二分式问卷等得到的不同类型数据采用参数法或非参数法[21- 22],如对支付卡法,较多根据所得离散型数据,采用中位值或平均值计算方法,即所评估环境物品的年人(户)均支付意愿WTP值选择累计频度为50%的支付额度或被调查者平均支付额度乘以适中的人群范围总人数得出研究区域生态价值。传统的生态服务价值分类计算方法其科学依据尚存争议[23- 25];一般处理CVM法调查数据方法所得平均支付意愿或中位数反映的是数据集中趋势[26- 28],而对于被调查者对平均支付意愿等分析结果认可度如何、对分析结果邻近额度是否意味着完全不认可等问题则不能从科学角度给予有说服力的回答。本文以杭州湾国家湿地公园海涂湿地生态服务价值估算为例,使用支付卡梯级法得到区间型数据,着眼于相同价格对于不同模糊子集隶属度大小,用“适中”价格隶属度刻画社会认可度,基于隶属函数的不断改进依次建立3种模糊统计模型进行比较研究,根据不同方法所得研究结果的一致性程度及与国内外研究成果对比以评估结果的可信度。结果显示一致性较好,并能方便地得出论域内每一价格的社会认可度,对上述问题的回答具有一定的参考价值。
1 研究区域与研究方法
1.1 研究区域概况
杭州湾国家湿地公园(30°10′N—30°42′N,120°55′E—121°30′E)位于杭州湾新区内,总面积为4350hm2,属杭州湾南岸慈溪三北滩涂湿地区域。地处北亚热带南缘,属海洋性季风气候,四季分明。年日照时数2048.4h,太阳年辐射总量468608J/cm2,平均温度16℃,无霜期244d,年降水1273mm。杭州湾国家湿地公园是杭州湾新区地域内开发建设以后主要的生态功能区,是西伯利亚、澳大利亚东亚候鸟迁徙路线中的重要驿站,是世界濒危物种黑脸琵鹭和黑嘴鸥的重要越冬地与迁徙停歇地之一。杭州湾湿地公园现吸引的鸟类已达220种,每年有上百种、几十万只候鸟途经杭州湾国家湿地公园。据观测,其中有列入世界自然保护联盟IUCN中国受威胁鸟类名录鸟类和国家重点保护野生动物名录鸟类分别有9种和13种。记录到底栖动物56种、鱼类42种、高等植物281种、浮游植物192种。
1.2 研究方法
1.2.1 引导评估技术
在CVM调查中,获得受访者的WTP/WTA的引导评估技术主要有:投标博弈法、开放式问卷法、支付卡法、封闭式问卷法(即二分式问卷DCQ)等,其中DCQ包含单边界二分法(DCQ)和双边界二分法(DCQ)。支付卡法和二分式问卷方法应用比较广泛,近年来,又出现在支付卡法和双边界二分法基础上提出的改进方法,即支付卡梯级法和1.5边界二分法[22,29- 30]。与在支付卡上仅选出一个特定 WTP 的支付卡法相比,支付卡梯级法是请受访者在支付卡上选择两个数值:一个是肯定能够接受的最低值,一个是肯定不能接受的最高值,因而降低了受访者的认知难度,避免了猜测或任选的现象[21,31]。基于此优点,本研究采用支付卡梯级法为引导评估技术。
1.2.2 问卷设计和调查过程
杭州湾国家湿地公园生态系统服务价值CVM调查时间为2016年2月至8月,调查分为两个阶段,第一阶段为预调查阶段,首先在杭州湾新区采用支付卡方式进行了预调查,目的在于确定预设的投标起点值、价格数值间隔以及范围的合理性,尽可能减小起点偏差。预调查共回收有效问卷106份,价格分布范围和形态基本确定,研究的初步结果可以作为本次研究的预调查形式。第二阶段采用支付卡梯级法进行调查,采用面对面采访的方式于2016年3月—8月在杭州湾国家湿地公园周边杭州湾新区、庵东镇、新浦镇、长河镇、小曹娥镇范围内进行抽样调查,要求受访者在独立认真考虑“价格适中”的含义后,给出“适中”价格区间。问卷采用随机抽样的方法,共发放问卷600份,问卷发放数量兼顾与研究区域的地理位置关系和人口数量,其中在研究区域所属行政区域杭州湾新区发放问卷300份,其余各镇发放75份。剔除无效问卷(前后矛盾,错答乱答,重要信息回答不全等)后,得到有效样本数据513份,相应得到“适中”价格区间作为样本值。
调查问卷共分为4个组成部分。第一部分是对杭州湾国家湿地公园海涂湿地的区域范围、湿地生态状况的历史变迁和生态功能进行介绍,并对调查问卷中涉及的相关事项进行提示;第二部分是包括对研究区的了解程度、对环保的关心程度、对湿地保护与开发的态度、湿地与受访者生活的相关性;第三部分是问卷的核心部分,是对支付卡梯级法问卷支付意愿的引导。问题为:根据上述杭州湾国家湿地公园海涂湿地生态系统服务价值简介,您认为每年该区域海涂湿地生态系统服务价值范围为:[]—[]。附加说明:单位为人民币元/平方米,第一个空格填价格下限,第二个空格填价格上限。研究组参考已有国内滨海湿地生态价值研究结果,上下限一般在闭区间1—20元 m-2s-1范围内取值。第四部分是受访者个人基本信息的调查问卷。发放全部采用面访调查方式。
1.2.3 偏差分析
CVM作为一种“事先”陈述偏好价值评估法,容易在操作上、统计上或心理上等方面产生偏差。为尽量避免由CVM引起的假想偏差、信息偏差、支付方式偏差 、投标设计偏差或投标起点偏差、调查方式偏差、策略性偏差、不反映偏差、问题顺序偏差、抗议投标偏差、积极性回答偏差、部分-整体偏差、替代偏差等,其中,假想的市场规则和投标设计的准确性是条件价值评估的主要限制条件[30- 32]。根据国际上的研究经验,本研究参考 1993年由美国大气与海洋局(NOAA) 提出的15条CVM设计原则[33],采取相应方法严格操作问卷设计、调查、处理等过程,以减少或有效避免条件价值评估中的各种偏差对估值结果的可能影响。
本次 CVM研究可能存在的主要偏差及其控制措施:
(1)假想偏差。该偏差是导致CVM的存在不确定性的最重要因素之一,出现的原因是受访者对假想市场问题的反应与真实市场的反应差异引起。本研究采用了强调海涂湿地的重要性及其生态服务价值的基本构成、提醒受访者的收入限制、反复调整设计通俗易懂的问卷设计、较大范围预调查和匿名调查方式等国际上通用的减少假想偏差的做法。
(2)投标起点偏差。该偏差引起回答范围偏离的原因是调查者所建议出价起点的高低会被受访者误解为“适中”的WTP范围,而通过预调查确定合理的投标起点值和数值间隔及范围是最有效的控制方法。本研究通过充分重视调查反馈而调整支付起点、支付数值间隔及范围并充分参考现有国内东南沿海滩涂湿地生态服务价值研究成果来减少起点偏差。
(3)信息偏差。为受访者提供的相关环境信息是否适中和充分将明显影响受访者对其 WTP的正确表达。本文所做调查要求被试人员对“杭州湾国家湿地公园生态系统服务价值”这一概念熟悉,以同时适应模糊统计调查实验的要求[34]。因此选取在研究区域周边至少生活了6个月且初中文化程度以上居民作为调查对象;且在此之前,调查者对受访者关于研究区域的生态服务价值做了详尽的介绍,内容包含生态服务价值的分类、研究组对研究区生态服务的物质量、能值量和价值的计量结果。在介绍研究区滩涂湿地的价值与功能时图文并茂,以使受访者对湿地的历史和现状有直观的认识,并与中国其他滨海湿地生态价值做了比较。
(4)积极性回答偏差。该偏差由面对面采访时因受访者为“作出让调查者感到满意的选择”而引起。本研究通过给受访者有充分独立的思考时间、向被调查者强调调查的理论探索研究性质来有效避免该偏差。
2 模型建立及求解
美国控制论专家L.A.Zadeh教授于1965年首次提出模糊集合的概念,用于刻画由于客观事物的差异之间存在着中介过渡导致的“模糊性”,也即客观事物中的不分明性和不确定性。把普通集合中的绝对隶属关系加以扩充,使元素对“集合”的隶属度由只能取0、 1 二值,扩展到可取闭区间[0,1]中的任意实数,从而实现定量刻画模糊性事物,处理问题的关键是模糊隶属度的刻画[34]。在CVM中,受访者对调查员给出的每一个价格数字,往往会判断此价格对相应资源价值是偏高、适中或是便宜,进而决定取舍。价格以价值为基础,同时受多因素影响,价格往往围绕价值上下波动。易见价格是一个具有“模糊性”的概念,给定一个特定的价格论域,价格“便宜”、“适中”和“昂贵”是三个模糊子集。与普通集合论概念不同,对于模糊集合中的子集,是没有明确边界的。如对于元素单位为10元 m-2a-1,考虑它隶属于“便宜”、“适中”或“昂贵”的大小和比较。下面建立的3个模糊统计模型均围绕“隶属度”的差异和改进而展开。
2.1 模型1 模糊统计模型
为了建立模糊集“价格适中”的隶属函数A(x),本文构建如下模糊统计模型:
首先界定模糊统计实验的要素:以海涂湿地单位面积价格做论域U=[0,100],单位为:元 m-2a-1;U中的随机运动经典集A*;U中的一个以A*为弹性边界的模糊子集“适中价格”A,制约着A*的运动。
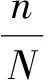
下求模糊集“价格适中”的隶属函数A2(x)。首先,鉴于从调查样本值得到最小数据为2,最大数据为20,于是,以0.5为起点,为20.5终点,以1为长度,做20个区间的划分,数据如表1所示。
然后,以价格为横坐标,相对频率为纵坐标画直方图,分析“适中价格”隶属函数A2(x)曲线的走势,模糊统计隶属分布图具有明显的正态分布特征(图1)。
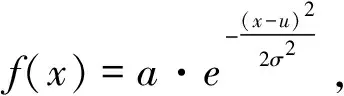
拟合结果如表2,从中可知,拟合函数均值参数为10.28,R-Square接近1,RMSE接近0,拟合效果较好。
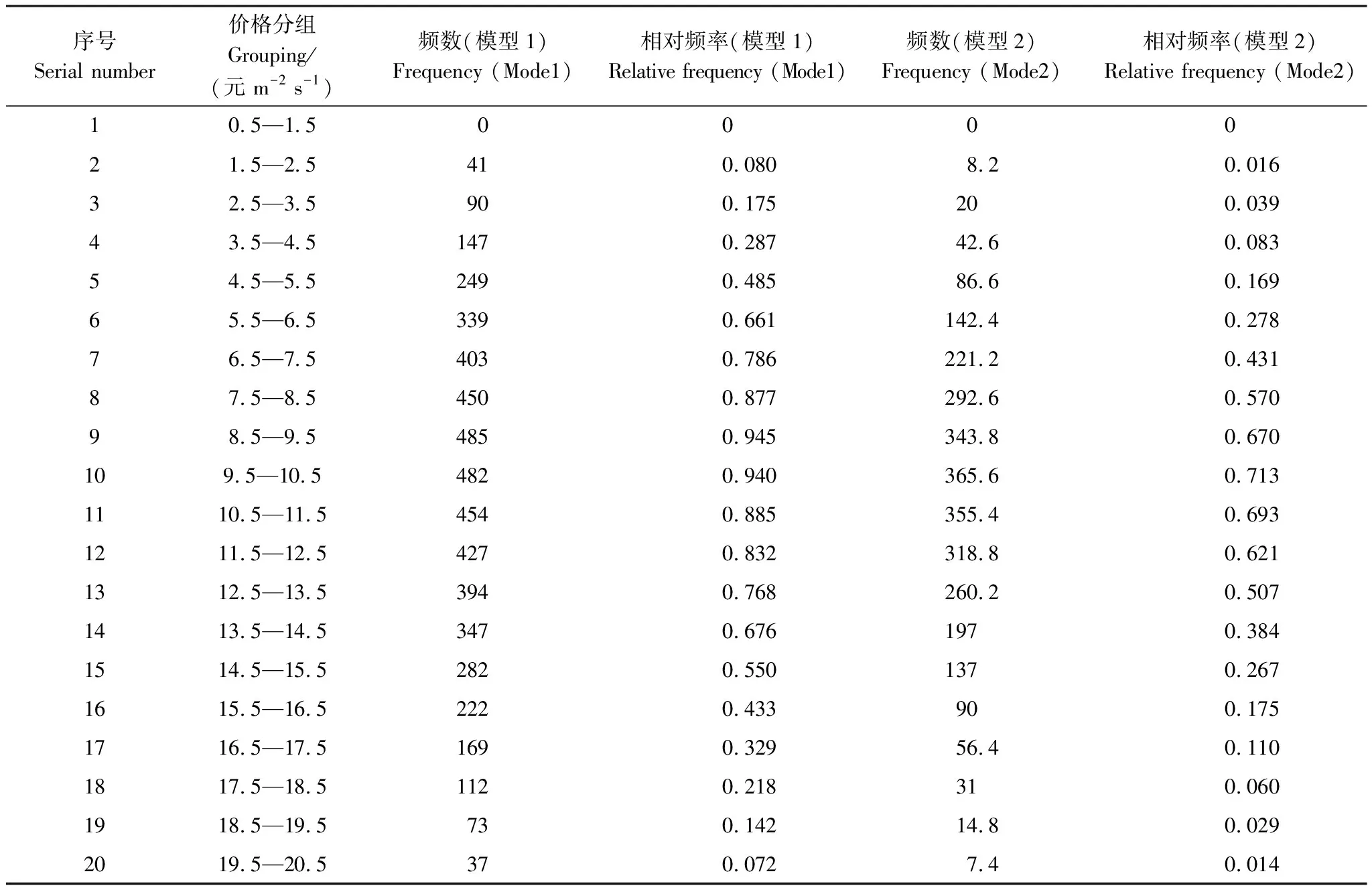
表1 模型1和模型2相对频率计算
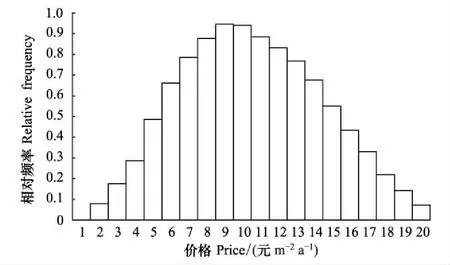
图1 模型1相对频率直方图Fig.1 Relative frequency histogram of model 1
2.2 改进的模糊统计
传统的模糊统计方法把区间内的数据“一视同仁”。比如,被调查者给出适中价格区间为[2,6],对于区间内的整数2、3、4、5、6,均统计1次。此方法直接导致“适中”价格的隶属函数直方图阶跃跨度比较大,光滑度不够。
事实上,被调查者潜意识里总是认为区间中间的数据隶属度要高于区间两端数据的隶属度[36]。基于此,改进传统模糊统计法如下:对原始统计数据区间均匀划分为若干段,对每一段赋予不同的权重。本文借鉴社会调查和心理测验等领域最常使用的态度评价形式即李克特量表(Likert Scale)的通常做法,采用五级评价制和等差赋分方法[37]。根据专家咨询结果,不同部分与评价域中心距离越近赋权应越大,反之则越小,这点不同于李克特量表采用对评价域升序赋分的方法。比如,对于价格区间[10,20],划分成长度相等的5部分: [14,16],[13,14)∪(16,17], [12,13)∪(17,18], [11,12)∪(18,19], [10,11)∪(19,20],取公差为0.2,分别赋予权重1、0.8、0.6、0.4、0.2。对于一般价格区间数据[a,b]中的元素x,x的权重ω(x)如下:

表2 拟合参数和拟合优度
a,u,σ是拟合隶属度函数的三个参数;SSE是拟合数据和原始数据误差的平方和,越接近0,说明模型拟合越好;R-square衡量了拟合在解释数据变化方面的成功程度,值越接近1说明模型拟合越好; Adjusted R-square 是调整过自由度的R-square,值接近1表示更适合,它通常是衡量拟合质量的最佳指标;RMSE指均方根误差,值接近0表示更适合
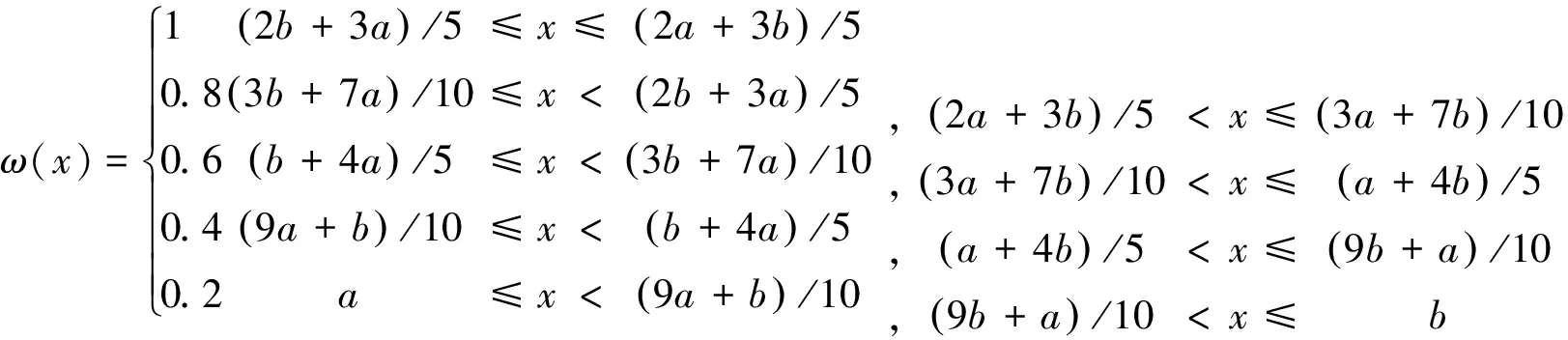
按此法得到的频数和相对频数见表1。
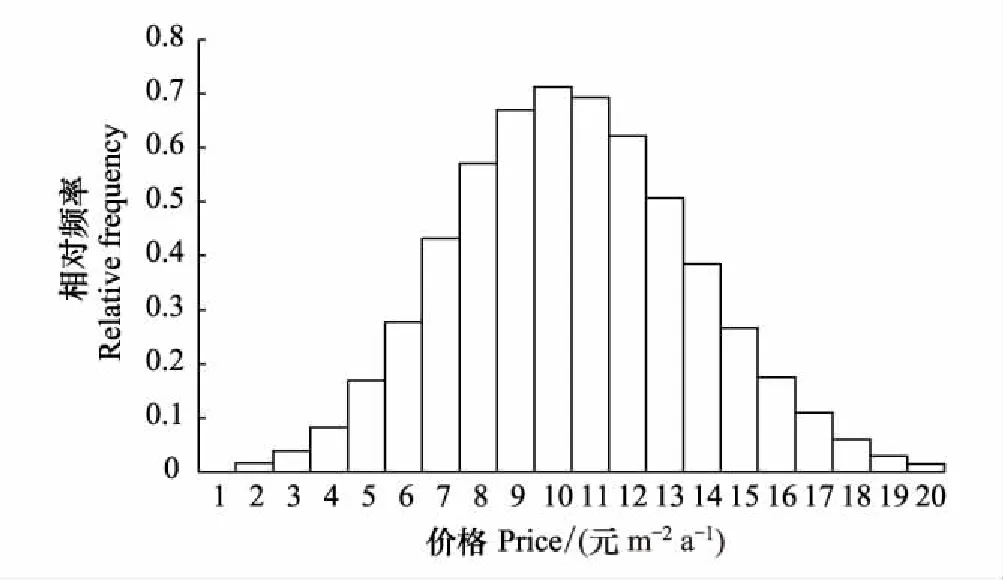
图2 模型2相对频率直方图Fig.2 Relative frequency histogram of model 2
同上得到以价格为横坐标、相对频数为纵坐标的直方图如上图2,可见,隶属度曲线更加光滑。同样用非线性最小二乘法拟合隶属度曲线得各参数见表2。由表2可知,拟合函数均值参数为10.38,R-Square=0.9973>0.9777,RMSE=0.01413<0.05135,改进的模糊统计方法拟合效果更好。
如表3,对比两个模型发现,模型2的隶属度比模型1隶属度变化要平缓。
2.3 三相定价法
上述两个模型仅仅构造了“适中”价格模糊集及其离散型隶属函数,事实上,被试针对湿地生态价值给出价格范围,比如为a—b元,可以认为被试对论域进行了连续三相划分,即便宜(小于a元)、适中(a—b元)、昂贵(大于b元)。下面建立滨海湿地生态服务价格三相划分的连续隶属度函数。
2.3.1 F统计实验
设论域为U,Ai均为U上的模糊集,Tm为相集,
Tm={A1,A2,…,Am}
如果每次实验的结果都能确定一个映射
e:U→Tm
称这样的实验为对Tm的m相模糊统计实验。
多相统计其目的是得到各相在论域U上的隶属函数。它们具有如下性质[28]:
∀u∈U,A1(u)+A2(u)+…+Am(u)=1。
2.3.2 三分法确定湿地生态服务隶属函数
假定环境物品的价格范围域为X,每一次问卷调查都确定一个映射f:X→R3,R3={A1=便宜,A2=适中,A3=昂贵}。假设ξ为便宜与适中的分界点,η为适中与昂贵的分界点,则每次模糊实验均确定论域U的一次划分,每次对X的划分确定一对数(ξ,η)。反之,给定(ξ,η),也确定了映射,能对模糊概念明确化,即区分了便宜、适中和昂贵。
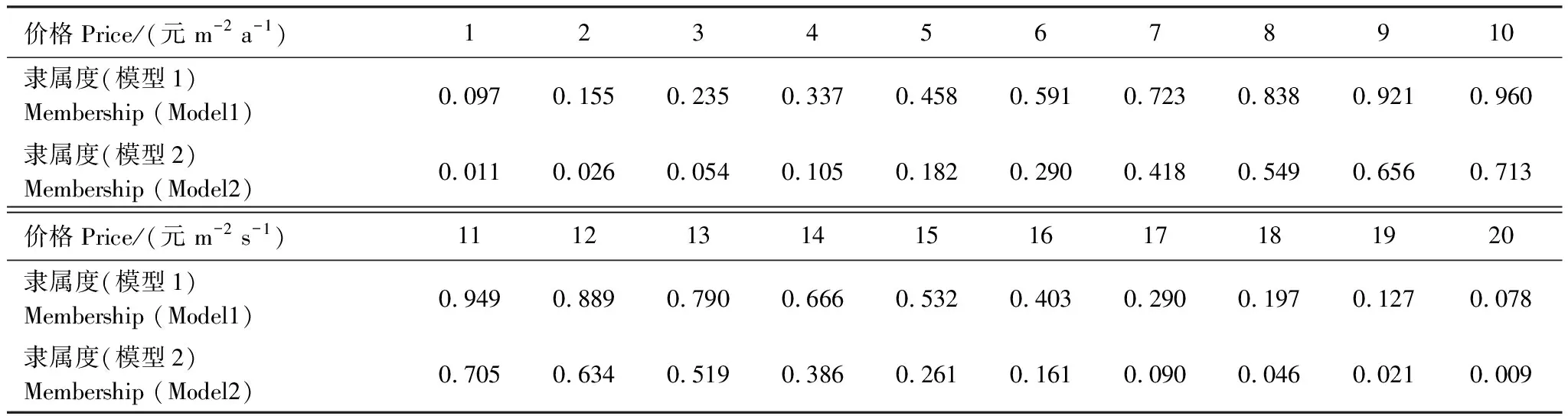
表3 模型1和模型2隶属度的比较
由于便宜、适中和昂贵的区间是随机区间,从而ξ和η是随机变量,数对(ξ,η)确定映射
f(ξ,η):U→{A1,A2,A3}
如果(ξ,η)满足p(ξ≤η)=1,则
下面求解各模糊集的隶属函数,先求模糊集A1的隶属函数μA1(x)。
在一次问卷中,当且仅当x≤ξ且x≤η,x隶属于模糊集A1。在n次问卷中,x对A1的隶属频率就是事件(x≤ξ,x≤η)发生的频率,从而得到A1的隶属函数:μA1(x)=P(x≤ξ,x≤η)[34]。
设(ξ,η)的联合密度函数为f(ξ,η),同时满足p(ξ≤η)=1,那么
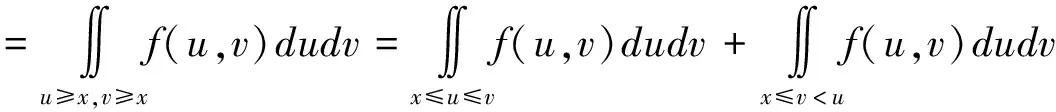
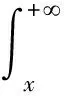
同理可求模糊集A3的隶属函数μA3(x):
在一次问卷中,当且仅当x>ξ且x>η,x隶属于A3。在n次问卷中,x对A3的隶属频率就是事件(x>ξ,x>η)发生的频率,从而得到A3的隶属函数:μA3(x)=P(x>ξ,x>η)。
设(ξ,η)的联合密度函数为f(ξ,η),同时满足p(ξ≤η)=1,那么
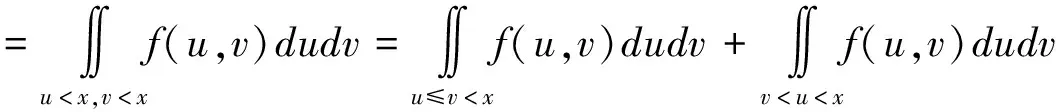
2.3.3 验证ξ,η满足的分布
对于统计调查得到的数据,可以利用统计方法验证其服从的分布。
使用MATLAB中的曲线拟合工具箱,发现ξ近似服从高斯分布或者威布尔分布,相应ξ的概率密度函数为:
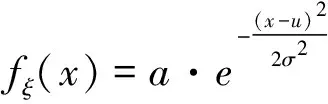
利用非线性最小二乘法,拟合情况如表4,从表可知高斯分布拟合优度更理想。
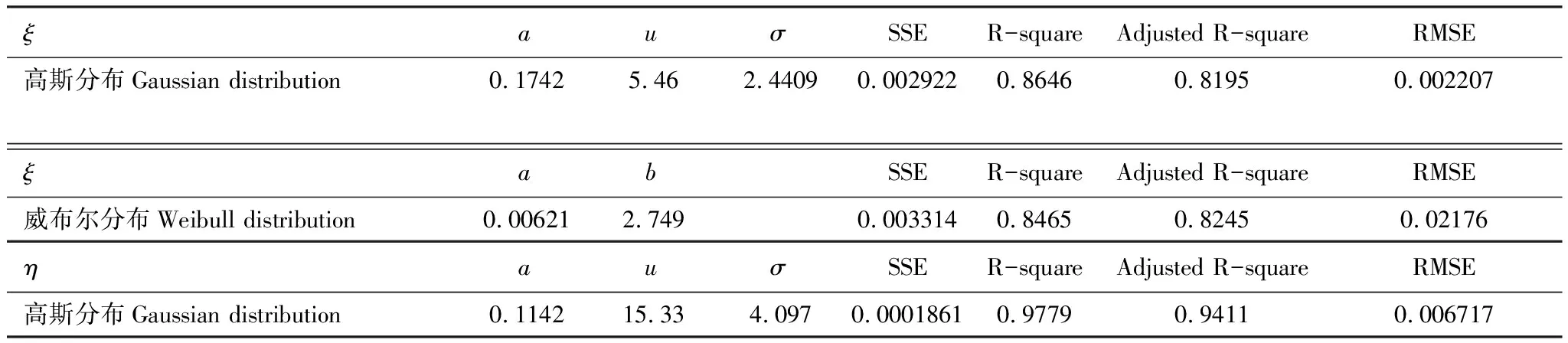
表4 拟合结果和拟合优度对比
同理使用MATLAB中的曲线拟合工具箱,发现η近似服从高斯分布,其概率密度函数各参数如表4。
由于
其中u1、σ1分别为ξ的均值和标准差;u2、σ2分别为η的均值和标准差。
从而
μA2(x)=1-μA1(x)-μA3(x)
当得到价格上下限(ξ,η)的均值u1,u2和标准差σ1,σ2后,可以确定滩涂资源价格的隶属函数曲线。
2.3.4 计算滩涂的适中价格
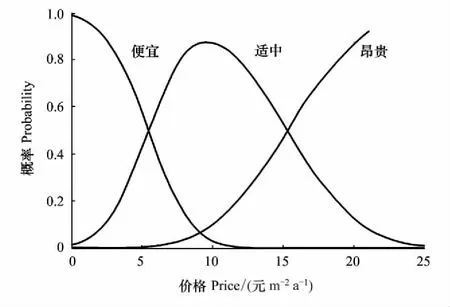
图3 价格的隶属函数曲线Fig.3 Membership function curve of price
利用MATLAB软件,把价格“便宜”、“适中”、“昂贵”的隶属函数图形呈现在同一坐标系中,如图3。从图像可知,滩涂价格适中的范围在区间[5.46,15.33]上。左端点是“便宜”模糊集隶属函数曲线和“适中”模糊集隶属函数曲线交点,右端点是“昂贵”模糊集隶属函数曲线和“适中”模糊集隶属函数曲线交点。滩涂适中的价格为9.76,认可度达到87.42%。该价格是“适中”价格隶属度曲线的最高点。对于价格9.76,认为其“昂贵”的有8.63%,“便宜”的有3.95%。其中,适中价格具有“适中”价格隶属函数的最大隶属度;适中价格区间内部的每一点“适中”价格隶属函数值均高于“便宜”价格隶属函数值和“昂贵”价格隶属函数值。
3 结论与讨论
本文使用支付卡梯级法,以杭州湾湿地公园为例,得到区间型数据,视价格“便宜”、“适中”和“昂贵”为模糊集,基于不断改进的3种模糊统计模型,评估了该区域单位面积生态系统服务价值。传统模糊统计模型视“适中”价格区间里的每一个数有相同的隶属度,而事实上受访者潜意识里认为区间中间的数据隶属度要高于区间两端的数据,因此建立了“适中”价格区间“橄榄球式”赋权模糊统计模型;在三相划分模型中,根据数据的分布特征,求出价格“便宜”、“适中”、“昂贵”的连续型隶属函数曲线,从而得出具有“适中”价格的点估计(适中价格)和区间估计(适中价格区间)。结果显示:3种方法得到的单价分别为10.28、10.38、9.76元 m-2a-1,其中三相划分模型同时得出了价格适中区间为[5.46,15.33]。三者一致程度较高。由表5可知,与国内使用CVM研究海涂湿地价值研究结果比较接近,略高于国外部分研究成果,高于全球潮滩湿地平均生态系统服务价值19580美元/hm2[13]。
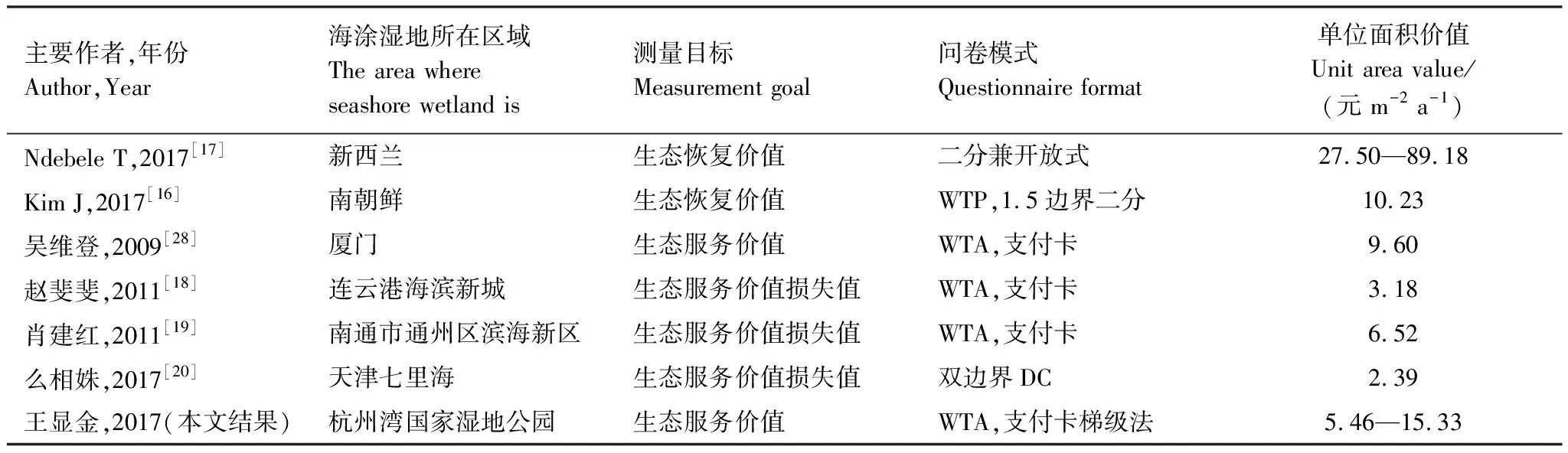
表5 本研究结论与部分国内外研究结论比较
在国内外生态服务价值分类评估技术不够完善和存在争议的情况下,分析了“生态价值”概念客观上的“模糊性”引致模糊数学模型的合理性;其次,鉴于传统模糊统计模型中对区间数据均匀赋权的不合理性,采用“橄榄球”式赋权建立赋权模糊统计模型,结果在隶属度函数的光滑性和拟合度上好于传统模糊统计模型的结果;第三,三相划分模型在拟合出三个模糊集隶属度函数的基础上,给出了“适中”价格的点估计和区间估计,也即给出了社会认可度最高的价格估计。利用本文的方法和结果也可以进一步探讨比较每一价格在人们心目中隶属于“便宜”、“适中”和“昂贵”的大小差异。
由于模糊统计模型要求对调查内容所涉及“适中”价格这一模糊概念有清楚的认识,对受访者文化程度规定了一定要求,这在一定程度上会影响样本的代表性。CVM调查问卷中给定了价格上下限的参考范围,这势必造成一定的测量偏差,参考了课题组前期研究成果和大量国内外滩涂湿地单位价值研究成果来纠正该偏差,所以本文建立的模型对于基于CVM法的生态资源价值评估具有借鉴意义。
参考文献(References):
[1] Daily G C. Nature′s Services: Societal Dependence on Natural Ecosystems. Washington DC: Island Press, 1997.
[2] 张天勇.生态支持战略:中国特色生态文明的进路.阅江学刊,2014,6(6):23- 27.
[3] 程敏,张丽云,崔丽娟, 欧阳志云.滨海湿地生态系统服务及其价值评估研究进展.生态学报, 2016, 36(23): 7509- 7518.
[4] Lovett A, Bateman I. Economic analysis of environmental preferences: progress and prospects. Computers, Environment and Urban Systems, 2001, 25(2): 131- 139.
[5] Bateman I J, Langford I H, Jones A P, Kerr G N. Bound and path effects in double and triple bounded dichotomous choice contingent valuation. Resource and Energy Economics, 2001, 23(3): 191- 213.
[6] 张志强,徐中民, 程国栋. 条件价值评估法的发展与应用. 地球科学进展, 2003, 18(3): 454- 463.
[7] 王伟,陆健健. 三垟湿地生态系统服务功能及其价值.生态学报, 2005, 25(3): 404- 407.
[8] 朱泽生,孙玲.东台市滩涂生态系统服务价值研究. 应用生态学报, 2006, 17(5): 878- 882.
[9] 王萱,陈伟琪,张珞平,郭伟.同安湾围(填)海生态系统服务损害的货币化预测评估. 生态学报, 2010, 30(21): 5914- 5924.
[10] 李睿倩,孟范平.填海造地导致海湾生态系统服务损失的能值评估——以套子湾为例.生态学报, 2012, 32(18): 5825- 5835.
[11] 宁潇, 邵学新, 胡咪咪, 吴明. 杭州湾国家湿地公园湿地生态系统服务价值评估. 湿地科学, 2016, 14(5): 677- 686.
[12] 王显金,钟昌标.沿海滩涂围垦生态补偿标准构建——基于能值拓展模型衡量的生态外溢价值.自然资源学报, 2017, 32(5): 742- 754.
[13] Costanza R, d′Arge R, de Groot R, Farber S, Grasso M, Hannon B, Limburg K, Naeem S, O′Neill R V, Paruelo J, Raskin R G, Sutton P, van den Belt M. The value of the world′s ecosystem services and natural capital. Nature, 1997, 387(6630): 253- 260.
[14] Prayaga P, Rolfe J, Stoeckl N. The value of recreational fishing in the Great Barrier Reef, Australia: a pooled revealed preference and contingent behaviour model. Marine Policy, 2010, 34(2): 244- 251.
[15] Engle V D. Estimating the provision of ecosystem services by Gulf of Mexico coastal wetlands. Wetlands, 2011, 31(1): 179- 193.
[16] Kim J, Lim S Y, Yoo S H. Public willingness to pay for restoring destroyed tidal flats and utilizing them as ecological resources in Korea. Ocean & Coastal Management, 2017, 142: 143- 149.
[17] Ndebele T, Forgie V. Estimating the economic benefits of a wetland restoration programme in New Zealand: a contingent valuation approach. Economic Analysis and Policy, 2017, 55: 75- 89.
[18] 赵斐斐,陈东景,徐敏,肖建红.基于CVM的潮滩湿地生态补偿意愿研究——以连云港海滨新区为例.海洋环境科学, 2011, 30(6): 872- 876.
[19] 肖建红,陈东景,徐敏,于庆东.围填海工程的生态环境价值损失评估——以江苏省两个典型工程为例.长江流域资源与环境, 2011, 20(10): 1248- 1254.
[20] 么相姝,金如委,侯光辉. 基于双边界二分式CVM的天津七里海湿地农户生态补偿意愿研究. 生态与农村环境学报, 2017, 33(5): 396- 402.
[21] Hanemann M, Kanninen B. The statistical analysis of discrete-response CV data//Bateman I J, Willis K G, eds. Valuing Environmental Preferences: Theory and Practice of the Contingent Valuation Method in the US, EU, and Developing Countries. New York: Oxford University Press, 1999: 302- 441.
[22] 张茵,蔡运龙.用条件估值法评估九寨沟的游憩价值——CVM方法的校正与比较.经济地理, 2010, 30(7): 1205- 1211.
[23] Mcdonough S, Gallardo W, Berg H, Trai N V, Yen N Q. Wetland ecosystem service values and shrimp aquaculture relationships in Can Gio, Vietnam. Ecological Indicators,2014,46(6), 201- 213.
[24] 徐筱越,乔冠宇.西部主体功能区生态补偿的均等化财政转移支付研究——以广西北部湾经济区三区县为例.广西财经学院学报,2015,28(06):42- 45.
[25] 崔丽娟,庞丙亮,李伟,马牧源,孙宝娣,张亚琼. 扎龙湿地生态系统服务价值评价.生态学报,2016,36(03):828- 836.
[26] 肖怡,陈尚,曹志泉,夏涛,郝林华.基于CVM的山东海洋保护区生态系统多样性维持服务价值评估.生态学报,2016,36(11):3321- 3328.
[27] 范紫娟,敖长林,毛碧琦,陈红光,王旭东.基于陈述性偏好法的三江平原湿地生态保护价值比较.应用生态学报,2017,28(02):500- 508.
[28] 吴维登, 张长宽. 厦门市滩涂价值的模糊测算. 水利经济, 2009, 27(2): 9- 11.
[29] EFTEC. Valuing Preferences for Changes in Water Abstraction from the River Ouse, Report to Yorkshire Water Services Ltd. Bradford, 1998.
[30] Hammitt J K, Graham J D. Willingness to pay for health protection: inadequate sensitivity to probability? Journal of Risk and Uncertainty, 1999, 18(1): 33- 62.
[31] 张志强,徐中民,程国栋,苏志勇.黑河流域张掖地区生态系统服务恢复的条件价值评估. 生态学报, 2002, 22(6): 885- 893.
[32] 蔡志坚,杜丽永,蒋瞻.条件价值评估的有效性与可靠性改善——理论、方法与应用. 生态学报, 2011, 31(10): 2915- 2923.
[33] National Oceanic and Atmospheric Administration. Report of the NOAA panel on contingent valuation. Federal Register, 1993, 58(10): 4601- 4614.
[34] 谢季坚,刘承平.模糊数学方法及其应用. 武汉: 华中科技大学出版社, 2014.
[35] 赵静,但琦.数学建模与数学实验(第三版).北京: 高等教育出版社, 2008.
[36] 张明,陈楠,吴陈.一种改进的模糊统计方法.华东船舶工业学院学报: 自然科学版, 2004, 18(4): 58- 61.
[37] 亓莱滨.李克特量表的统计学分析与模糊综合评判. 山东科学, 2006, 19(2): 18- 23, 28- 28.
