基于改进熵权与灰色模糊理论的城市轨道交通PPP项目风险评价研究

王建波， 有维宝， 刘芳梦， 张 薇， 杨迪瀛

(青岛理工大学管理工程学院， 山东 青岛 266520)

0 引言

伴随着我国城市化的快速推进，城市轨道交通建设规模不断扩大，以政府为主导的资金筹措与管理模式已无法满足建设的资金需求。PPP(public-private-partnership)是指由私营部门为基础设施项目进行融资和建设，并在未来一段时间内运营项目，通过充分发挥公共部门与私营部门各自的优势，以提高公共产品和服务的效率，实现资金最佳投资价值的模式[1]。将PPP模式引入城市轨道交通建设，能有效解决政府资金筹措问题。但城市轨道交通PPP项目具有工程量大和施工环境复杂等特点，使得PPP项目面临的风险复杂，因此，需要进行合理的风险评价，以保证PPP项目的正常运作。

鉴于PPP项目风险评价的重要性，针对此问题国内外学者进行过大量研究。Thomasctal等[2]和Ernest等[3]分别采用故障树和传统案例分析方法对风险水平进行评价，并提出相应的风险分担机制； 赵磊等[4]、宋博等[5]和冯辉红等[6]在确定风险评价指标的基础上，分别构建集成FAHPFCE、熵权模糊理论以及灰色聚类的风险评价模型，并用实例进行验证； 高云莉等[7]和胡芳等[8]针对公共工程项目风险，分别建立动态模糊与VIKOR的数学模型，对风险进行定量评价； 李强等[9]和陈斌等[10]在PPP项目风险指标评价方面均采用AHP方法，并提出相应的风险控制措施； 李妍等[11]和张璞等[12]依据具体实际案例建立不同的风险评价指标体系，并分别采用模糊层次分析与变权思想对评价模型进行优化。

上述研究从不同评价角度建立风险指标体系，并采用动态模糊等理论构造数学模型对项目风险进行定量研究。然而，现有研究未考虑项目全生命周期不同阶段变化所带来的风险差异，往往将风险看作一个整体； 风险指标权重常采用单一的AHP法或熵权法等确定，使得风险评价常有片面性； 运用数学模型对不同领域PPP项目进行风险研究，但专门针对城市轨道交通PPP项目风险评价还不太成熟。针对以上不足，本文首先采用Delphi法有效识别城市轨道交通PPP项目风险，考虑风险阶段变化性建立评价指标体系； 其次指出传统熵权法的不足并进行改进，结合层次分析法构造最优数学模型，求解主客观综合权重； 构建灰色聚类分析与模糊评判法相结合的综合风险评价模型，并运用到青岛地铁3号线实际案例中，验证模型合理性的同时评判城市轨道交通PPP项目的风险等级。

1 城市轨道交通PPP项目风险识别

城市轨道交通PPP项目风险是指项目在全生命周期内各阶段所产生的不确定性对项目总目标的影响。合理风险评价的前提是对风险进行有效识别。美国项目管理协会(PMI)定义风险识别为： 确定有可能影响项目的风险事件的过程[13]。在以往风险识别研究中，文献[4, 8, 10]将PPP项目风险概括为外部、内部及项目自身因素3个层面； 文献[9]对铁路PPP项目风险因素进行识别，将风险划分为系统风险与非系统风险2类； 文献[11]和文献[14]按风险来源不同将PPP项目风险划分为宏观、中观及微观层面风险。风险识别方法也较为多样，主要有Delphi法、头脑风暴法以及检查表法等。

本文研究的城市轨道交通PPP项目规模大、建设周期长，在全生命周期内风险具有阶段变化性，需要对风险进行持续而动态的识别。Delphi法是一种反馈调查法，在匿名方式基础上使各位专家独立做出判断，适合大型PPP项目，因此，选用Delphi法识别城市轨道交通PPP项目各阶段的关键风险。在文献[5, 15-16]对风险按阶段划分的研究成果基础上，邀请20位相关领域专家对风险进行识别，从立项、融资、建设和运营4个阶段出发，结合各阶段共同存在的风险，构建城市轨道交通PPP项目风险评价指标体系。风险识别过程与风险评价指标体系构建如图1和图2所示。

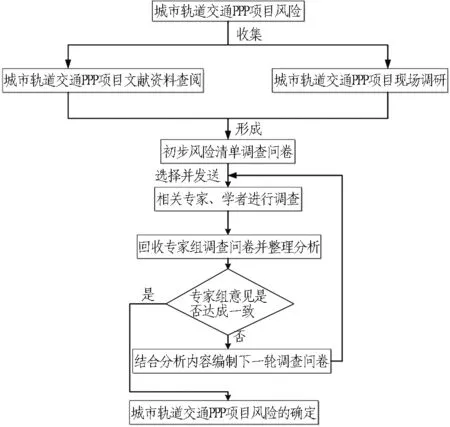
图1 城市轨道交通PPP项目风险识别过程

图2 城市轨道交通PPP项目风险评价指标体系

2 城市轨道交通PPP项目灰色模糊综合评价模型构建

灰色模糊综合评价法是一种在“贫信息”情况下，评判模糊因素现象或事物的方法。其中在模糊数学基础上形成的模糊综合评价法，将不易定量描述的因素定量化，并评价该因素的隶属等级状况。则在灰色系统理论中占有重要地位的白化权函数用来刻画一个灰数对其取值范围内不同数值的偏爱程度[17]，对各数据点隶属于某灰类或灰数的程度进行定量描述。

由于城市轨道交通PPP项目建设周期长，不同阶段的风险因素与评价等级难以定量描述，使风险评价具有模糊性特征，需要借助模糊理论进行研究。采用Delphi法识别城市轨道交通PPP项目风险，识别结果会受到专家主观经验制约，导致风险之间关系及形成因素不够明确，使风险评价指标体系具有灰色性。本文构建的灰色模糊综合评价模型对研究城市轨道交通PPP项目风险有较好的适用性，可以有效解决风险评价过程中模糊性与灰色性的问题。

2.1 指标权重的确定

指标权重的准确计算在风险评价中占有重要地位。单独采用层次分析法或熵权法求得的结果均不全面，为充分兼顾评判者的主观意愿和指标的客观重要性，本文采用改进熵权法与层次分析法相结合的方法来确定城市轨道交通PPP项目风险指标权重。

2.1.1 传统熵权法计算过程

2.1.1.1 数据标准化处理

设有k个城市轨道交通PPP项目风险指标x1，x2，...，xk，邀请城市轨道交通领域相关专家对指标进行评估，用xij′表示第j个专家针对第i个指标的评估概率，形成相应的风险评价矩阵Y′，并对其进行标准化处理，得到标准化矩阵Y。

2.1.1.2 计算各指标信息熵

2.1.1.3 确定指标权重

由信息熵计算公式可得各风险指标的信息熵为E1，E2，...，Ek，利用式(1)可计算第i个指标的客观权重。

(1)

2.1.2 熵权法的改进

在传统的熵权法计算中，当信息熵值Ei→1时，利用式(1)，计算结果会出现信息熵值的微小变化引起指标熵权成倍变化的情况。如：当信息熵值分别为E1=0.99,E2=0.98,E3=0.97时，E1/E2≈1,E2/E3≈1，但利用式(1)求出熵权值W1=0.166 7,W2=0.333 3,W3=0.500 0，此时W1/W2≈1/2,W2/W3≈2/3。根据熵权基本原理，信息熵与熵权提供的信息量应保持一致，当信息熵数值差距微小时，计算出的熵权值不应出现太大差距，然而上述现象明显与熵权原理相违背。针对以上问题，将熵权计算公式改为

(2)

2.1.3 改进熵权法与层次分析法结合

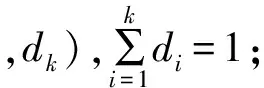
(3)

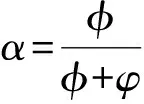
2.2 评价灰类及白化权函数的确定

灰类确定是否合理将直接影响PPP项目风险评价的准确性。根据城市轨道交通PPP项目自身特点，可将评价灰类确定为5个等级，为很低、低、中、高、很高，并分别赋值1、3、5、7、9。在以往研究的基础上，结合城市轨道交通PPP项目风险特征，构建每一灰类对应的白化权函数，如表1所示。

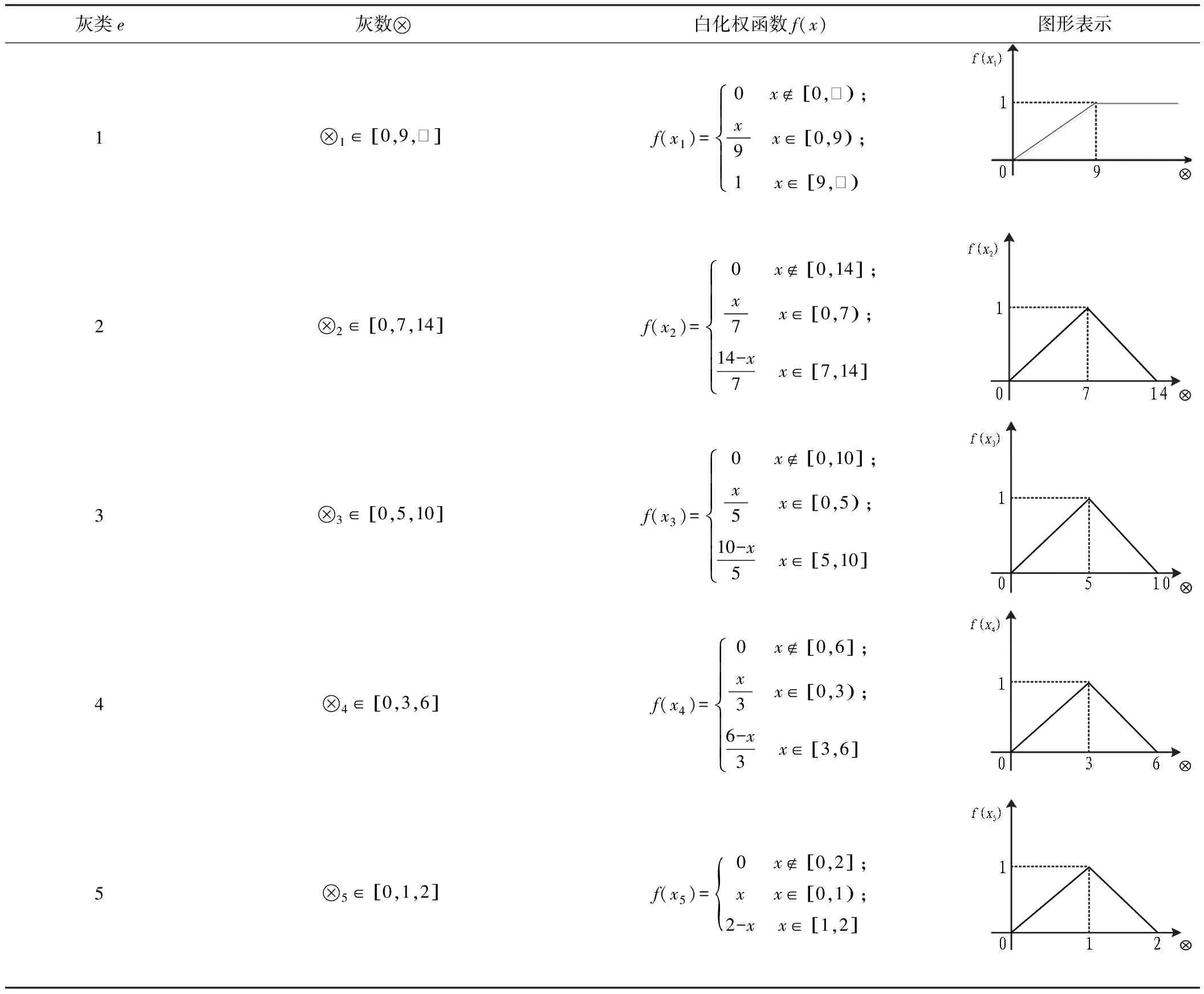
表1 城市轨道交通PPP项目风险评价白化权函数

2.3 灰色评价系数及权矩阵计算

2.3.1 确定样本矩阵

邀请15位城市轨道交通及风险管理领域相关专家对上述风险指标进行评估打分。评分标准如下： 评分范围取0—9，其中分值1、3、5、7、9分别代表风险等级很低、低、中、高、很高，2、4、6、8则表示介于上述等级中间，最终得到专家评价的样本矩阵。

2.3.2 灰色评价系数的计算

用yije表示第e类评价灰类的灰色评价系数，

(4)

式中：t为评审专家人数，将5大灰类数值进行综合，进而得到灰色评价总系数公式。

(5)

2.3.3 灰色评价权矩阵的计算

用cije表示第e类评价灰类的灰色评价权，

(6)

本文灰类确定为5个等级，将各灰类评价权进行综合，得到灰色评价权向量Cij=(cij1,cij2,cij3,cij4,cij5)，进而得到灰色评价权矩阵C。

2.4 模糊综合评价计算

首先，对灰色评价权矩阵Ci做综合评价。使用改进熵权法与层次分析法相结合计算权重的方法，得出2级指标层权重向量为Hi，评价结果用Bi表示。

Bi=Ci×Hi=(bi1,bi2,bi3,bi4,bi5)。

(7)

得到关于2级指标层的灰色评价权矩阵

其次，对灰色评价权矩阵B作综合评价。由上述权重计算方法可得1级指标层主客观综合权重为S=(s1,s2,...,si)，评价结果用A表示，则

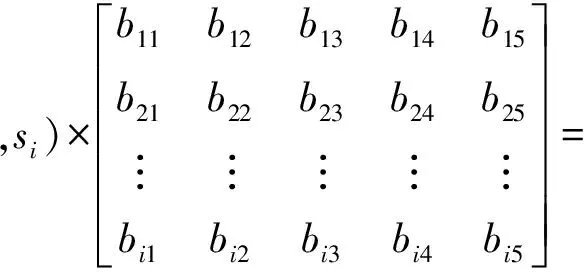
(a1,a2,a3,a4,a5)。

(8)

最后，对灰类划分的5个等级按“灰水平”赋值，灰类等级值向量用U表示，即U=(9,7,5,3,1),得到灰色综合评价值为

G=A×UΤ。

(9)

将计算结果与评判等级相对应，判定城市轨道交通PPP项目的风险等级。

3 实例分析

为验证所构建灰色模糊综合评价模型的合理性和有效性，选取青岛地铁3号线进行实例验证。作为山东省境内建成的第1条地下铁路，青岛地铁3号线由青岛地铁集团等多方共同融资建造，于2010年6月进入施工阶段，2016年12月全线开通运营，线路总长25.2 km，横跨青岛市南、市北和李沧3个市辖区。针对项目建设规模大、面临风险错综复杂的特点，运用改进熵权的灰色模糊综合评价模型，判定该项目的风险等级。

3.1 风险指标体系的构建

以函件的方式向20位城市轨道交通及风险管理领域相关专家进行征询，采用Delphi法对城市轨道交通PPP项目全生命周期各个阶段风险进行识别，最终将PPP项目风险划分为5大类阶段风险与相对应的21类指标风险，具体构建风险指标体系如图2所示。

3.2 风险指标权重的确定

在已构建指标体系的基础上，邀请城市轨道交通PPP项目风险管理相关领域15位专家进行打分，确定风险指标概率，并分别采用层次分析法与改进熵权法计算权重，利用构建的最优数学模型(式(3))计算得出主客观组合权重。

1级指标层B权重向量：S=(0.143 6,0.164 2,0.263 8,0.243 3,0.185 1)。

2级指标层C权重向量：

H1=(0.334 2,0.379 6,0.286 2)；

H2=(0.385 6,0.376 2,0.238 2)；

H3=(0.268 7,0.173 4,0.213 6,0.237 9,0.106 4)；

H4=(0.293 6,0.154 7,0.090 0,0.323 4,0.138 3)；

H5=(0.267 9,0.313 3,0.196 3,0.124 7,0.097 8)。

3.3 评价灰类及白化权函数的确定

根据城市轨道交通PPP项目风险特点，将评价灰类划分为5个等级，每一灰类对应的白化权函数分别为f(x1)、f(x2)、f(x3)、f(x4)、f(x5)，如表1所示。

3.4 灰色评价系数及权矩阵计算

首先，确定样本矩阵。邀请15位相关领域专家以0—9范围为标准对上述风险指标进行打分，最终获得城市轨道交通PPP项目风险指标评分统计如表2所示。

其次，计算灰色评价系数，以审批获得/延误风险指标C11为例，将相应专家评价分值带入各灰类白化权函数中，计算结果如表3所示。

利用式(4)计算得C11风险指标对应5大灰类灰色评价系数分别为3.999 6，5.143 0，7.200 0，11.333 5，2.000 0，进而由式(5)计算得灰色评价总系数yij=29.676 1。

最后，计算灰色评价权矩阵。利用式(6)计算并将各灰类评价权综合，得C11风险指标对应的灰色评价权向量C11=(0.134 8,0.173 3,0.242 6,0.381 9,0.067 4)。同理，计算其他指标的灰色评价权向量。最终得到1级指标B1对应的灰色评价权矩阵

利用上述计算方法得1级指标B2、B3、B4、B5分别对应的灰色评价权矩阵C2、C3、C4、C5。

3.5 模糊综合评价计算

首先，对灰色评价权矩阵Ci进行综合评价，已计算2级指标层C对应的权重向量为Hi，利用式(7)得到对应的灰色评价权向量分别为：

B1=H1×C1=(0.109 9,0.141 3,0.197 8,0.322 3,0.228 7)；B2=H2×C2=(0.131 2,0.168 7,0.236 1,0.354 8,0.109 1)；B3=H3×C3=(0.182 0,0.233 8,0.287 5,0.270 9,0.025 9)；B4=H4×C4=(0.191 3,0.238 9,0.283 5,0.251 1,0.035 2)；B5=H5×C5=(0.153 4,0.194 7,0.250 7,0.302 4,0.098 8)。

其次，对灰色评价权矩阵B进行综合评价，1级指标层对应的权重向量为S=(0.143 6,0.164 2,0.263 8,0.243 3,0.185 1)，利用式(8)得到最终综合评价权向量为

A=S×B=(0.143 6,0.164 2,0.263 8,0.243 3,0.185 1)×

(0.160 3,0.203 8,0.258 4,0.293 1,0.084 4)。

最后，计算灰色综合评价值。根据式(9)计算得到城市轨道交通PPP项目风险综合评价值为

G=A×UΤ=(0.160 3,0.203 8,0.258 4,0.293 1,

0.084 4)×(9,7,5,3,1)T=5.125。

将实例研究结果与划分的风险等级相对应，得出该项目风险等级为“中等”。通过综合权向量计算可知，项目风险比重由大到小依次为运营阶段风险、建设阶段风险、融资阶段风险、立项阶段风险及各阶段共存风险。为保证项目可行性需要，采取相应的风险应对措施。针对运营阶段风险，项目公司应根据运营成本向政府提出相应票价补偿，保证票价的合理性，并引入先进运营管理经验，规避运营成本超支等风险。针对建设阶段风险，应选择资质较好的项目承包商，严格控制质量和工期，合同中应考虑项目变更因素，合理规避完工及成本超支等建设风险。其他阶段风险应加强跟踪与反馈，综合运用风险转移和风险分割等策略，提高项目成功率。实例分析也验证了所构建的灰色模糊综合评价模型具有可行性与合理性，能帮助投资者对风险进行准确评价和针对性管理，以降低项目整体风险。

表2 城市轨道交通PPP项目风险指标评分表

表3C11风险指标灰色评价系数及权向量计算结果

Table 3 Risk index grey evaluation coefficientC11and weight vector calculation results

评分各灰类白化权函数f(x1)f(x2)f(x3)f(x4)f(x5)30.333 30.428 60.600 01.000 00.000 020.222 20.285 70.400 00.666 70.000 030.333 30.428 60.600 01.000 00.000 030.333 30.428 60.600 01.000 00.000 040.444 40.571 40.800 00.666 70.000 020.222 20.285 70.400 00.666 70.000 010.111 10.142 90.200 00.333 31.000 030.333 30.428 60.600 01.000 00.000 030.333 30.428 60.600 01.000 00.000 020.222 20.285 70.400 00.666 70.000 010.111 10.142 90.200 00.333 31.000 020.222 20.285 70.400 00.666 70.000 020.222 20.285 70.400 00.666 70.000 030.333 30.428 60.600 01.000 00.000 020.222 20.285 70.400 00.666 70.000 0总计3.999 65.143 07.200 011.333 52.000 0评价权0.134 80.173 30.242 60.381 90.067 4

4 结论与讨论

本文采用Delphi法以及灰色模糊综合评价模型，对城市轨道交通PPP项目风险进行全面有效的识别及科学合理的评价，并借助改进熵权法与层次分析法相结合的方法确定主客观权重，对青岛地铁3号线实际案例的风险等级进行判定，并得出以下结论： 1)从风险指标权重及最终综合评价权向量数值可以看出，运营阶段风险与建设阶段风险所占比重较大，对这2个阶段应给予更多关注并采取相应的风险应对措施； 2)青岛地铁3号线风险综合评价值表明此项目整体风险等级为“中等”，项目处于良好的可控状态； 3)针对城市轨道交通PPP项目全生命周期构建的风险评价指标体系以及改进熵权与层次分析相结合计算权重的方法具有科学性和适用性，在PPP项目风险评价中引入灰色模糊综合评价模型，保证评价全面合理性的同时，可为今后城市轨道交通PPP项目风险评价研究提供参考。但本文对于具体风险应对措施的研究还不够全面，故在后续研究中有待补充针对性的风险应对措施，以便提供更准确和科学的决策，进而更好地控制城市轨道交通PPP项目风险。

参考文献(References):

[1] 刘婷, 王守清, 盛和太, 等. PPP项目资本结构选择的国际经验研究[J]. 建筑经济, 2014, 35(11): 11.

LIU Ting, WANG Shouqing, SHENG Hetai, et al. Research on international experiences of capital structure in PPP projects[J]. Construction Economy, 2014, 35(11): 11.

[2]THOMASCTAL A V, SATYANARAYANA. Modeling and assessment of critical risks in BOT road projects[J]. Construction Management and Econonmics, 2006, 24(4): 407.

[3]ERNEST E A, ALBERT P C. Indentifying public partner-ship(PPP) risks in managing water supply projects in China[J]. Journal of Facilities Management, 2013, 11(2): 152.

[4] 赵磊, 屠文娟. 集成FAHPFCE的中国PPP项目风险评价[J]. 科技管理研究, 2011(2): 80.

ZHAO Lei, TU Wenjuan. Risk assessment of China′s PPP projects based on integration of FAHP and FCE [J]. Science and Technology Management Research, 2011(2): 80.

[5] 宋博, 武瑞娟, 牛发阳. 基于OWA与灰色聚类的城市轨道交通PPP融资风险评价方法研究[J]. 隧道建设, 2017, 37(4): 435.

SONG Bo, WU Ruijuan, NIU Fayang. Research on risk evaluation method of PPP financing mode for urban rail transit based on OWA and grey clustering method[J]. Tunnel Construction, 2017, 37(4): 435.

[6] 冯辉红, 魏晶晶, 杨可, 等. 熵权-模糊评价法在BT公路项目风险评价中的应用研究[J].公路, 2016,61(1): 170.

FENG Huihong, WEI Jingjing, YANG Ke, et al. Entropy weight-fuzzy evaluation method applied to risk assessment of BT road project[J]. Highway, 2016, 61(1): 170.

[7] 高云莉, 李宏男, 张国军. 基于合作的工程项目风险动态模糊评价[J]. 大连理工大学学报, 2010, 50(3): 404.

GAO Yunli, LI Hongnan, ZHANG Guojun. Dynamic fuzzy evaluation of construction project risk based on collaboration[J].Journal of Dalian University of Technology, 2010, 50(3): 404.

[8] 胡芳, 刘志华, 李树丞. 基于熵权法和VIKOR法的公共工程项目风险评价研究[J]. 湖南大学学报(自然科学版), 2012, 39(4): 83.

HU Fang, LIU Zhihua, LI Shucheng. Research on the risk appraisal of public project based on entropy method and VIKOR method[J]. Journal of Hunan University(Natural Sciences), 2012, 39(4): 83.

[9] 李强, 韩俊涛, 王永成, 等. 基于层次分析法的铁路PPP项目风险评价[J]. 铁道运输与经济, 2017, 39(10): 7.

LI Qiang, HAN Juntao, WANG Yongcheng, et al. Risk evaluation of railway PPP project based on AHP[J]. Railway Transport and Economy, 2017, 39(10): 7.

[10] 陈斌, 王蕾, 刘群英. 基于AHP-熵值法的PPP项目风险评价模型研究[J]. 工程管理学报, 2017, 31(2): 126.

CHEN Bin, WANG Lei, LIU Qunying. Modle research on risk evaluation of PPP project based on AHP-entropy method[J]. Journal of Engineering Management, 2017, 31(2): 126.

[11] 李妍, 赵蕾. 新型城镇化背景下的PPP项目风险评价体系的构建——以上海莘庄CCHP项目为例[J]. 经济体制改革, 2015(5): 17.

LI Yan, ZHAO Lei. Construction of PPP project risk assessment system under background of urbanization: A case study of Haixinzhuang CCHP Project[J].Reform of Economic System, 2015(5): 17.

[12] 张璞, 王丽萍, 李荣波. 基于相对风险模型的公私合作项目风险评价研究[J]. 技术经济与管理研究, 2016(11): 3.

ZAHNG Pu, WANG Liping, LI Rongbo. RRM-based research on risk assessment of PPP project[J]. Technoeconomics & Management Research, 2016(11): 3.

[13] 乌云娜, 胡新亮, 张思维. 基于ISM-HHM方法的PPP项目风险识别[J]. 土木工程与管理学报, 2013, 30(1): 67.

WU Yunna, HU Xinliang, ZHANG Siwei. Risk identification of public-private-partnership project based on ISM-HHM method[J]. Journal of Civil Engineering and Management, 2013, 30(1): 67.

[14]LI B. Risk management of construction public private partnership projects[D]. Glasgow: Glasgow Caledonian University, 2003.

[15] 刘维庆, 邓少波, 顼志芬. 城市轨道交通项目融资风险动态评价[J]. 系统工程, 2016, 34(12): 153.

LIU Weiqing, DENG Shaobo, XU Zhifen. Dynamic evaluation of financing risk of urban rail transit project [J]. Systems Engineering, 2016, 34(12): 153.

[16] 赵辉, 董骅, 屈微璐. 构建基于改进系统动力学的环保PPP项目风险动态评价体系[J]. 财会月刊, 2017(27): 65.

ZHAO Hui, DONG Hua, QU Weilu. Dynamic evaluation system of environmental PPP project based on improved system dynamics [J]. The Accounting Issue, 2017(27): 65.

[17] 刘思峰, 党耀国, 方志耕, 等. 灰色系统理论及其应用[M]. 3版.北京: 科学出版社, 2004: 104.

LIU Sifeng, DANG Yaoguo, FANG Zhigeng, et al. Grey system theory and its application[M]. 3rd Edition. Beijing: Science Press, 2004: 104.

[18] 周惠成, 张改红, 王国利. 基于熵权的水库防洪调度多目标决策方法及应用[J]. 水利学报, 2007, 38(1): 100.

ZHOU Huicheng, ZHANG Gaihong, WANG Guoli. Multi-objective decision making approach based on entropy weights for reservoir flood control operation[J]. Journal of Hydraulic Engineering, 2007, 38(1): 100.