基于MCKD与小波包熵的齿轮箱轴承微弱故障信号提取*

杨 思，朱爱华，2，姚德臣 ，杨建伟,2 ，白永亮

(1.北京建筑大学 城市轨道交通车辆服役性能保障北京市重点实验室，北京 100044；2.北京交通大学 机械与电子控制工程学院 ，北京 100044)

0 引言

齿轮箱是地铁的关键部件。滚动轴承在齿轮箱中大量使用，并为其提供稳定的支撑。在设备的运行中大部分能量都要通过齿轮箱进行调节和控制，因而滚动轴承的工作状态将会直接影响到整套设备运行安全[1-2]。由于地铁齿轮箱所处环境恶劣且启动频繁，轴承转速变化剧烈，并且随着载客量的变化也会影响齿轮箱负载的变化，这就很容易造成齿轮箱发生故障，严重影响地铁的安全运行。因此，研究地铁齿轮箱的故障信号提取方法具有重大的意义。

对于含噪的非平稳、非线性故障信号，许多学者提出了不同的降噪算法。钟先友[3]等通过最大相关峭度解卷积与重分配小波尺度谱相结合的方法，有效地分离了旋转机械的故障信号中掺杂的噪声，提高了机械复合故障的诊断效率。白永亮[4]等提出了一种EMD-BSS改进算法，通过计算IMF分量的相关相关系数矩阵并进行地铁齿轮箱微弱故障振动信号的提取。唐贵基[5]等利用粒子群寻优算法确定了MCKD方法的核心参数，自适应地实现了最优的增强故障信号中冲击成分的效果。但是在采集的齿轮箱故障信号中含有的大量噪声，使用单一的最大相关峭度解卷积方法很难有效地分辨出隐含于环境噪声中的有用信息特征。Yi Wang[6]等通过小波包变换与谱峭度相结合的方法，准确提取了旋转部件故障产生的瞬时脉冲信号。史东锋[7]等针对在应用包络解调法对滚动轴承诊断中需要需要选定共振频带的问题，提出了一种通过提取不同的频带的调制频率并优化分解尺度的方法，应用该方法成功检测了滚动轴承的内外圈及滚子的局部缺陷。

本文提出MCKD和小波包熵值相结合的方法对地铁齿轮箱故障信号进行降噪处理，通过强化了信号中的有效冲击成分，以达到降低了噪声的干扰，并有效地提取故障信息的目的，而且提高了信噪比。

1 基本原理介绍

1.1 最大相关峭度解卷积原理

为了强化故障信号中的冲击特征，最大相关峭度解卷积方法是通过选取一个有限脉冲响应滤波器系数[8-9]，对信号进行降噪并使具有特定周期成分的相关峭度趋于最大值。从而在滤除干扰噪声的同时突出了轴承故障信号中具有连续脉冲特性的有用成分，使轴承故障信号的本质特征成分更容易提取。

对于周期为T的信号yn，其最大相关峭度定义为：

(1)

式中，f=[f1f2…fL]T为滤波器系数，L表示有限冲击响应滤波器的长度，M为移位数,一般取1～7，为了提高该方法对高频成分的检测能力,取M=7。

为了使相关峭度CKM(T)最大，必须筛选一个最优的滤波向量f，所以构造如下函数：

(2)

其中,k=1,2,…,L。于是可以通过求解方程(2)极值得到最优的滤波器系数f。求解结果：

(3)

其中，

通过上式可计算出滤波后的输出信号：

(4)

运用迭代方法求解最大相关峭度的数值计算过程：

(1)确定周期T、移位数M和滤波器长度L;

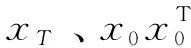
(3)根据式(4)计算出滤波后的输出信号y；

(4)根据输出信号y计算αm和β；

(5)计算新滤波器的系数f；

(6)比较ΔCKm(T)和ε的关系，当ΔCKm(T)>εmin时，转到第(2)步继续下一轮循环，否则跳出循环。其中ε是用来控制循环的最小正整数一般取0.01。

1.2 小波包熵及降噪理论

Shannon信息熵是一种依据信息花费最小原理，对信源的随机性和无规则程度的度量。信息量越大，不确定性越小，其熵值越小；信息量越小，不确定性越大，其熵值越大。

对于随机变量X其Shannon信息熵的定义为：

(5)

结合小波包分解方法与信息熵值理论可以得到不同分解节点信号的小波包熵Hij的定义为：

(6)

其中，ei,j是第(i,j)节点信号所包含有用信息的能量在第i层总能量中的所占的概率，j=0,1,2,…,2i-1。k为第(i,j)节点信号的区间长度。

因此，运用小波包变换和熵值相结合的方法对信号进行降噪，能够根据信号的特征，自适应地选择相应频带，使之与信号频谱相匹配，从而提高了信噪比。

小波包是小波的进一步发展[10-12]，其中小波变换的定义为：设x(t)是平方可积的函数，Ψ(t)为母小波函数，则

(7)

其中，a为尺度因子(a>0)，改变a的大小能够控制窗口的宽度和外形的变化，从而实现信号在频域内的移动，τ为平移因子，其值可负可正，改变τ的值能够改变窗口的位置，从而实现小波窗口在时域内的移动。通过式(7)可以看出小波具有多分辨特性。在实数空间给定相互正交的尺度函数φ(t)和小波函数ψ(t)满足下面的双尺度方程：

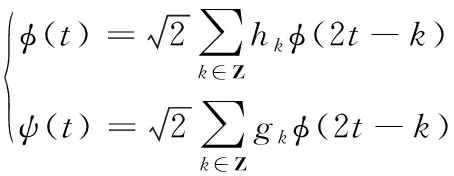
(8)

式中，hk、gk为正交滤波器组中滤波器系数。

为了使式(8)更具一般性，所以引入函数un(t)并令其满足如下的双尺度关系方程：

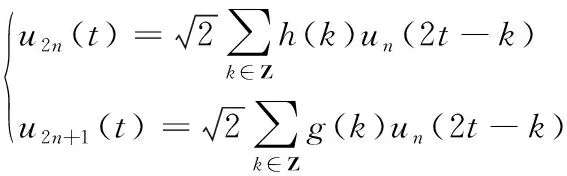
(9)

式中，h(k)与g(k)具有正交关系。当n=0时u0(t)和u1(t)分别退化为尺度函数与小波基函数。所以，由式(9)构造的函数集序列{un(t)}称为有尺度函数φ(t)确定的正交小波包。小波包分解三层分解原理图见图1。

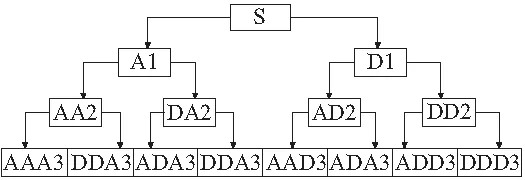
图1 小波包三层分解结构

基于以上论述，本文首先通过MCKD进行降噪，强化信号中的冲击成分。并对强化后的信号进行小波包熵值的二次降噪，更好地抑制了干扰噪声对有用信息提取的影响，提高了故障信号特征提取的效率，增加了故障诊断的准确性。其诊断流程如图2所示。

图2 故障诊断流程图

2 仿真信号分析

有损伤的齿轮与轴承在运转的过程中都会产生含有规律性的冲击成分的振动信号。为了验证本文所提出方法的有效性及稳定性，对模拟机械故障并带有冲击成分的信号进行分析。模拟信号的表达式为：

其中，冲击振幅y0=5，阻尼系数ξ=0.1，冲击故障发生的周期为0.01s,采样频率fs为20kHz，采样点数N=4096，故障特征频率f为100Hz。模拟信号时域波形如图3a所示。为了更加逼近实际工程中所遇到的故障振动信号，在仿真信号中加入强度位10dB的随机高斯白噪声，加入噪声后的仿真信号时域波形如图3b所示，从图中可以看出由于高斯白噪声存在，仿真信号中的冲击成分特征完全被淹没，故障特征的提取就会变得异常困难。因此，需要对含噪信号进行降噪处理，以降低噪声的影响。

(a)轴承局部故障仿真信号

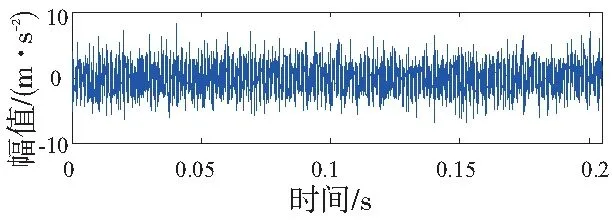
(b)含噪声的轴承局部故障仿真信号图3 仿真信号及含噪信号的时域波形

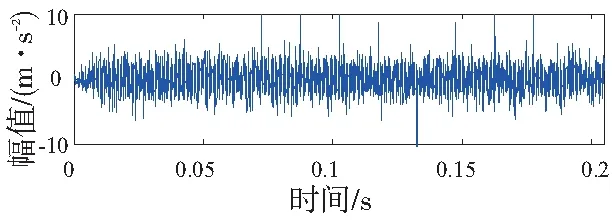
图4 MCKD 降噪后的波形图

首先对含噪的仿真信号进行MCKD降噪预处理，其结果如图4所示。从图中可以看出故障信号的冲击成分只有部分恢复，而且这些冲击成分难以表征轴承局部故障信号特征。需要利用小波包熵值对其进一步处理。依据经验对含噪信号进行3层小波包分解，末层各节点信号时域波形如图5所示。

图5 小波包分解末层节点信号波形图

通过对比末层各节点信号的相关系数、小波包熵值如表1所示。明显可以看出节点(3,1)与节点(3,3)信号的相关系数较大及小波包熵值较小，说明其含有用信息比较多。所以选用节点(3,1)与节点(3,3)信号进行小波包重构，重构信号如图6所示。从图中可以看出已经基本提取了原信号中的冲击成分，适合作为分析信号进行故障特征的提取。

表1 仿真信号末层各节点相关系数及小波包熵值

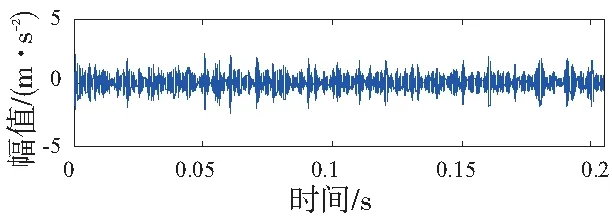
图6 小波包重构信号

对重构后的信号进行能量算子解调后的希尔伯特包络，结果如图7所示，从包络谱图中可以看出主要峰值为非常接近于100Hz及其倍频，这与仿真信号设置的特征频率相对应。证明了基于MCKD与小波包熵值相结合的方法能有效提取强背景噪声条件下的故障信号的本质特征。

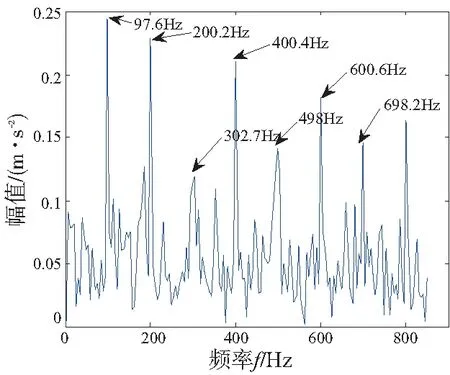
图7 MCKD-小波包熵降噪后的包络信号

3 实验与分析

实验轴承的型号为NU202ECP圆柱滚子轴承，在SpectraQuest公司生产的地铁专用齿轮箱实验台上对轴承振动加速度信号进行采集。该试验台是按照地铁实际齿轮箱结构尺寸的1/3进行设计，并能通过改变组装方式以获取不同的故障类型，相对真实的模拟了地铁在实际运行中齿轮箱中的轴承所出现的不同故障振动特性。该齿轮箱故障试验台如图8所示。在信号采集地过程中采用ICP加速度计作为传感器并安装于轴承座上，试验过程中使用的轴承为外圈完整，但是内圈人为的用电火花加工出的凹槽作为故障。NU202ECP轴承的具体参数为，轴承节径D为24.8mm，滚动体直径d为5.5mm，其个数n为11。在实验的过程中，输入轴转频fr为28Hz，采样频率为20480Hz，结合以上数据并根据轴承内圈故障频率计算公式(11)，得出本实验中所使用故障轴承的特征频率为188Hz。

(11)

图8 故障诊断实验台示意图

轴承内圈故障时传感器采集到的加速度波形如图9所示。有背景干扰噪声的存在很难直接从信号时域波形中提取内圈故障的特征信息。所以，运用与仿真信号相同的信号处理方法。首先对含噪振动信号进行MCKD降噪预处理，得到降噪后的时域波形如图10所示。从图中可以看出隐藏在噪声中的冲击成分得到了加强。但是残留的噪声依然干扰故障信号本质特征的提取，因此，需要对预处理后的振动信号进行二次降噪。运用小波包熵的方法对故障信号进行3层分解得到末层的8个节点信号如图11所示。并计算出末层各节点相关系数-熵值值如表2所示。从表中可以看出节点4与节点5相关系数及峭度值均相对较大。因此，选用前节点4与节点5信号进行重构。重构信号如图12所示，从图中可以明显的看出故障信号中的冲击成分。

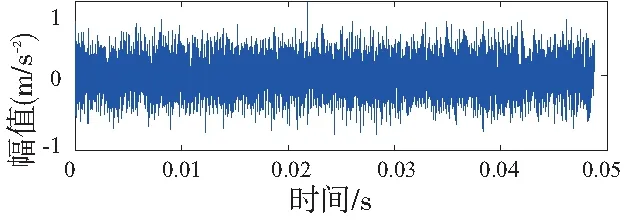
图9 轴承内圈故障信号

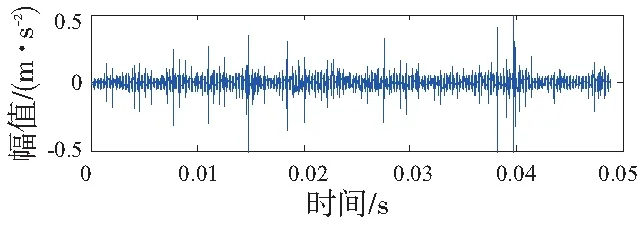
图10 MCKD去噪后的信号

图11 第3层各节点时域波形

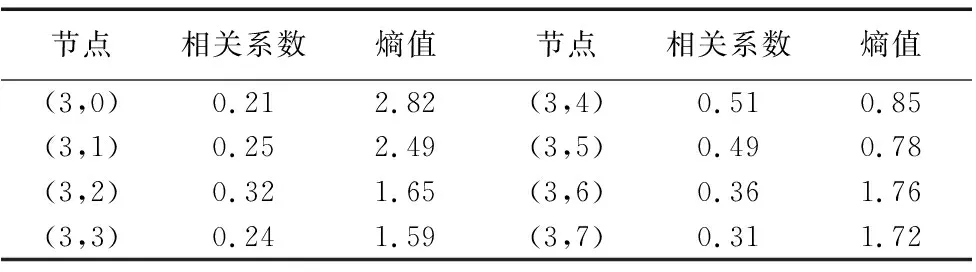
节点相关系数熵值节点相关系数熵值(3,0)0.212.82(3,4)0.510.85(3,1)0.252.49(3,5)0.490.78(3,2)0.321.65(3,6)0.361.76(3,3)0.241.59(3,7)0.311.72

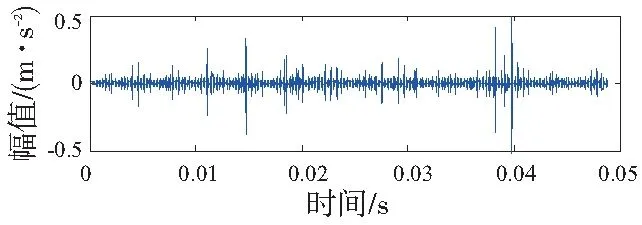
图12 节点重构信号

重构信号的能量算子包络谱如图13所示。

图13 重构信号包络谱

从图中可以清楚的看到频率27.5Hz，这与转频28 Hz极为相似，以及与轴承内圈故障的特征频率188Hz非常接近的188.8Hz及其相应的倍频分量。而对比未经试验台与本方法处理过的包络谱，如图14所示。可以明显

看出，故障特征频率完全被干扰噪声的频率覆盖。因此，基于MCKD分解与小波包熵相结合的方法能有效地滤除环境噪声对轴承故障信号本质特征提取的干扰，提高了的轴承故障诊断的正确率。

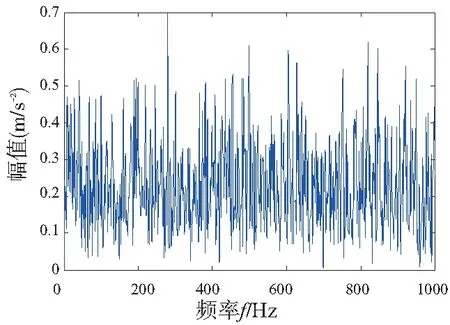
图14 未降噪信号的包络谱

4 结束语

实验结果分析表明，基于MCKD与小波包熵相结合的齿轮箱轴承微弱故障诊断方法，能准确地提取故障信号的本质特征，并得到如下结论：

(1)通过最大相关峭度解卷积对轴承故障振动信号进行处理，不仅有效地去除了噪声的干扰、加强了隐含于环境噪声下的少量冲击成分，而且提高了信噪比。通过计算可知，信噪比大约提高了10dB。

(2)对降噪后的信号进行小波包熵值分解并通过相关系数-峭度准则能获得含有更多故障信息的节点信号，再通过小波包重构和希尔伯特包络谱分析，可以准确提取反映轴承故障的微弱信号特征。

(3)MCKD和小波包熵值相结合的方法能够准确、全面地诊断出故障的特征信息，为地铁齿轮箱故障诊断提供了一种新方法。

[参考文献]

[1] 谢志勇. 基于DSP和BP神经网络的旋转机械在线故障诊断系统[J]. 仪表技术与传感器, 2011(3):64-66.

[2] 石明江, 罗仁泽, 付元华. 小波和能量特征提取的旋转机械故障诊断方法[J]. 电子测量与仪器学报, 2015(8):1114-1120.

[3] 钟先友, 赵春华, 田红亮,等. 基于自适应最大相关峭度解卷积和频率切片小波变换的齿轮故障特征提取[J]. 中国机械工程, 2014, 25(21):2880-2885.

[4] 白永亮, 杨建伟, 姚德臣,等. 基于改进EMD-BSS算法的地铁齿轮箱单通道轴承微弱故障特征提取[J]. 机械设计与研究, 2016(6):57-61.

[5] 唐贵基, 王晓龙. 自适应最大相关峭度解卷积方法及其在轴承早期故障诊断中的应用[J]. 中国电机工程学报, 2015, 35(6):1436-1444.

[6] Wang Y, Xu G, Lin L, et al. Detection of weak transient signals based on wavelet packet transform and manifold learning for rolling element bearing fault diagnosis[J]. Mechanical Systems & Signal Processing, 2015, 54-55:259-276.

[7] 史东锋, 鲍明, 屈梁生. 小波包络分析在滚动轴承诊断中的应用[J]. 中国机械工程, 2000, 11(12):1382-1385.

[8] 张晓涛, 唐力伟, 王平,等. 基于改进MCKD方法的声发射信号降噪[J]. 机械设计与研究, 2015，31(1)70-73,77.

[9] Mcdonald G L, Zhao Q, Zuo M J. Maximum correlated Kurtosis deconvolution and application on gear tooth chip fault detection [J]. Mechanical Systems & Signal Processing, 2012, 33(1):237-255.

[10] 王潜龙, 冯全科, 屈展,等. 基于声发射与小波包理论的压力管道泄漏检测[J]. 西安交通大学学报, 2003, 37(5):515-518.

[11] Davoodi S, Mostafapour A. Gas leak locating in steel pipe using wavelet transform and cross-correlation method[J]. The International Journal of Advanced Manufacturing Technology, 2014, 70(5):1125-1135.

[12] 于志伟, 苏宝库, 曾鸣. 小波包分析技术在大型电机转子故障诊断系统中的应用[J]. 中国电机工程学报, 2005, 25(22):158-162.