九轴数控微加工中心的轨迹生成及控制策略研究*

储 健，郭文探，张 军

(1.天津职业技术师范大学 自动化与电气工程学院,天津 300222；2.天津大学 电气与自动化工程学院，天津 300072)

0 引言

工程零件的小型化及微型化使得具有精密定位功能的多轴微加工中心受到了广泛的关注[1-3]，典型的应用有微型叶轮、微机电装置、表面织构和微模具等，传统具有串联运动学配置的机床存在主要构架的惯性累积，导致带宽及跟踪精度损失，采用气浮轴承尽管能够减小摩擦，但是又引入了新的成本问题和扰动刚度问题[4]。因此具有多自由度的机床成为解决此类问题的首选，多自由度机床能够在最少配置下获得不同的部件特征，在高进给速度下能够减少摩擦接触实现精密定位。

运动冗余机床曾被提出来通过额外的装置来实现无障碍工作区域和增强定位精度。Takeuchi提出采用无摩擦空气静力驱动来提高定位精度，给一台五轴机床增加第六根轴来微铣加工具有复杂形状的微小型器件[5]。Lu and Usman提出了一种六自由度的无摩擦磁悬浮高速工作台，具有较大的平面工作空间[6]。本文采用同样的磁悬浮原理设计一种具有六自由度的旋转台，同时结合一个三轴微机床构架了一个九自由度的微加工中心。

在微加工领域已经存在许多多轴加工机床的研究[7-8]，但是很少见到本文构架的运动冗余机床，Chio等人曾提出了相似的配置，但是其C轴旋转受限，约束其潜在定位能力[9]。本文构架的九自由度微加工中心相比之下定位能力增强，特别是C轴有所改进，机床可以加工微小形貌、自由曲面表面和不同微几何特征的表面。尽管一台五轴机床就可以加工复杂零件，但是额外的四轴可以带来更多的优势，例如几何与跟踪误差补偿，增大冗余轴的带宽，但是又引入了新的问题，如何解决不减少驱动器行程、速度、加速度和混合极限的条件下，结合额外的四轴来生成五轴平滑的速度和加速度刀具路径轨迹，这些问题还没有得到很好的解决。

目前针对无冗余配置和路径极限的路径规划已经有较多的研究[10-14]，但是冗余配置下的路径生成还没有完善的解决方案，本文提出的九自由度加工机床的构架及其轨迹生成算法和控制策略，不减少任何轴的行程、速度、加速度和混合极限，文中采用空间螺旋路径来验证本文提出的方法。

1 九轴微加工中心构架策略

九轴微加工中心由一个三轴机床基体支撑一个六自由度磁悬浮工作台组成，如图1所示，各轴由磁驱动线性电机，x,y和z轴的峰值力为364N，580N和458N，持续力为91N，145N和73N。每根轴沿着笛卡尔坐标系x,y,z移动的最大行程为100mm，插补编码器分辨率为40nm，加工中心z轴的空气主轴最大转速为200000rpm。磁力驱动器安装在微铣中心的X-Y平台上，如图1所示，旋转工作台的直线运动轴与微铣中心的平移轴平行，微铣中心的三轴与旋转工作台的六轴共同组成了九轴微加工中心。

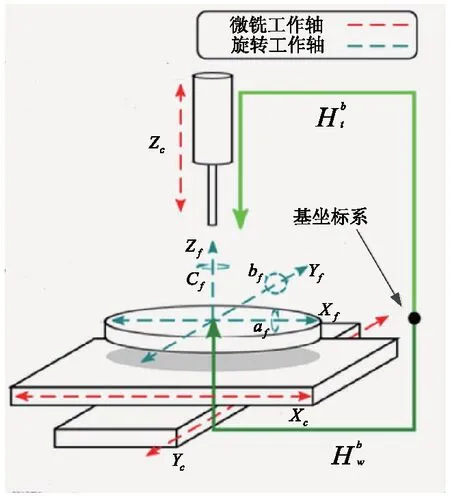
图1 九轴微铣加工中心及其运动链

微加工中心由单一的dSpace DS1103实时计算机控制，可以提供给微铣三个PWM通道和三个编码器通道来进行当前命令和位置反馈，提供给旋转工作台4个编码器通道，4个模数转换通道和8个数模转换通道。4个编码器通道测量旋转台的4个平移位置，8个数模转换通道需要控制4个三相线性放大器来驱动旋转台，因此整个加工中心是由7个编码器通道，3个PWM通道、8个数模转换通道和4个模数转换通道共同控制。通过内部控制模块在实时Matlab支持的dSpace数字信号处理面板上实施。

2 九轴微加工中心轨迹生成策略

2.1 正向运动学

(1)

其中，H(q)为刀具坐标系向工件坐标系的坐标转换矩阵，基坐标系向工件的逆坐标转换表示为：

(2)

其中，xcyczcxfyfzfafbfcf为微加工中心的驱动命令，为了简洁，缩短了三角术语，其中caf=cosaf,saf=sinaf,cbf=cosbf,sbf=sinbf,scf=sincf，基坐标系到刀具的转换矩阵为：

(3)

其中，zc为微加工中心的Z轴命令，计算图1中的转换矩阵H(q)为：

(4)

通过转换，可以通过九轴驱动位置向量q来表示刀尖的位置P(q)与刀具轴方向O(q)。

2.2 逆运动学

数控编程的刀位坐标命令通过逆运动学映射到驱动轴上，通过九轴微加工中心的雅可比矩阵J(q)来求解，雅可比矩阵通过求导式(1)的P(q)与O(q)获得：

(5)

雅可比矩阵将驱动位置的改变映射到刀具位置dR上：

dR=J(q)dq

(6)

J*=J(q)T(J(q)J(q)T)-1

(7)

对驱动位置的微分为：

(8)

式(8)的第一项给出了单位位移ds下所有轴的最小平均运动，第二项通过选择价值函数来保证所有轴不超越最大行程限位：

(9)

▽φ(q)为φ(q)的梯度。

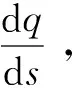
3 九轴微加工中心控制策略

将三轴微铣线性电机与六轴旋转工作台的磁力驱动悬浮质量分别控制。

3.1 线性电机控制

由刚体动力学建立位置X与磁力F的开环传递函数如下：

(10)

其中，M为移动部分的质量，B为粘滞力。

采用比例位置控制器级联比例-积分速度控制器来控制微铣的线性驱动，从给定的参考位置命令XR推导轴位置的闭环传递函数：

(11)

其中，Kp，Kv，Kvi分别为位置控制器增益，速度控制器增益及速度控制器的积分增益。选择增益使速度环和位置环的带宽为60Hz和20Hz。

3.2 旋转工作台控制

旋转工作台为自由悬浮质量，其位置X与磁力F之间的传递函数为：

(12)

其中，m平移轴运动部分的质量，式中传递函数的相位为-180°，相位在理想带宽下增加在下式的超前-滞后控制器上：

(13)

其中，K调整交叉频率，α调整要增加的相位，T调整相位增加后相应的频率。根据经验选取交叉频率为100Hz，增加相位为60°，结果形成的带宽大约为100Hz。采用超前-滞后控制器，旋转台轴的闭环传递函数为：

(14)

4 轨迹生成及控制策略

本文针对所提出的运动学和控制模型通过仿真与实验进行验证，每个轴的控制参数，质量以及摩擦力如表1所示。采用螺旋线刀具路径来测试本文研究的9轴微加工中心，刀具路径仿真及相应的位置命令如图2所示，实验所得的各轴跟踪误差如图3所示，微铣轴的跟踪误差在10μm以内，旋转工作台的直线运动的误差为1μm，旋转误差为20μrad。

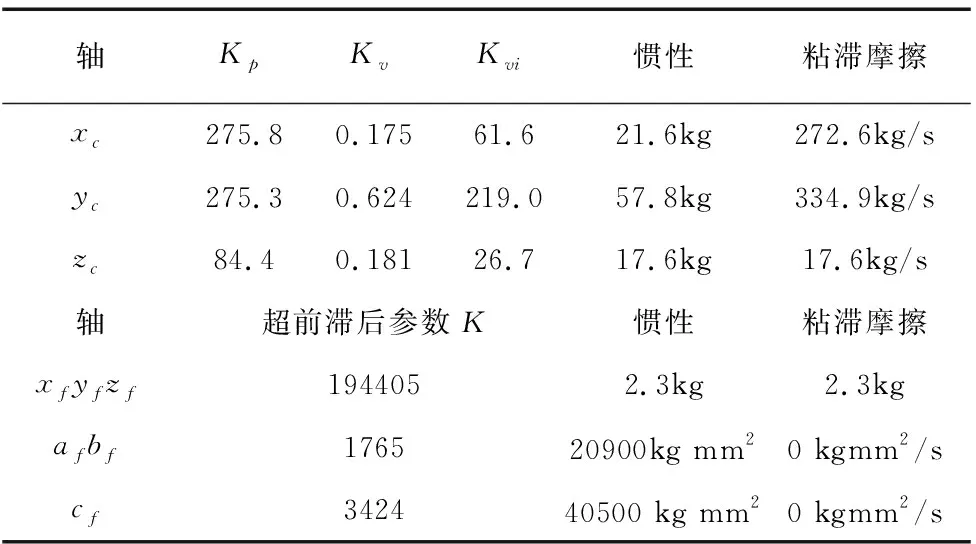
表1 九轴微加工中心控制参数

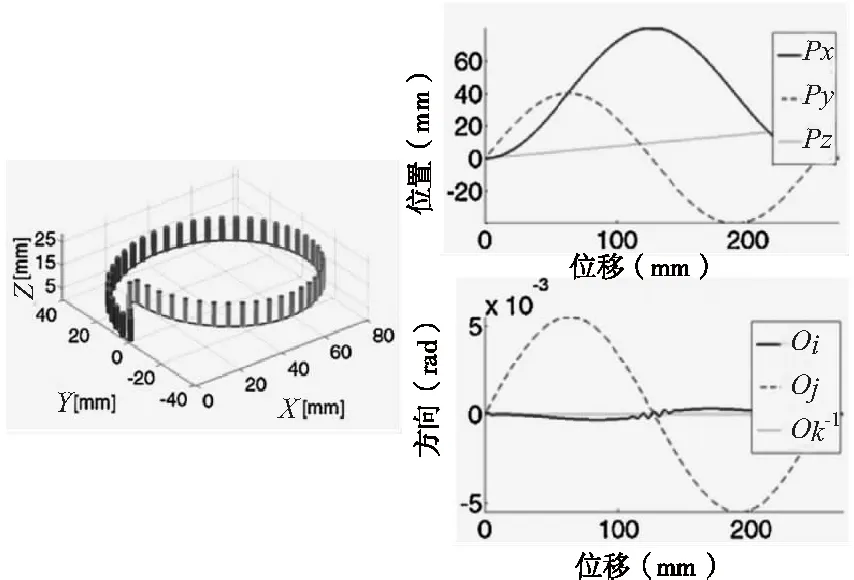
图2 螺旋线轨迹及位置与方向

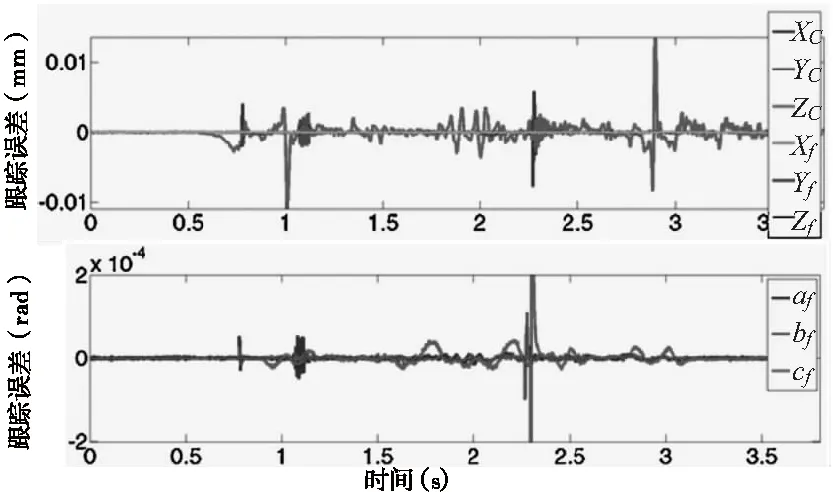
图3 微加工中心各轴的跟踪误差

本文提出的轨迹生成算法采用进给优化策略来确保规划的轨迹不超过驱动极限，当规划的轨迹接近极限位置时，需要优化以改进当前进给策略。

5 结论

本文提出了一种由三轴微铣和六轴旋转工作台组成的九轴数控微加工中心并研究其刀具轨迹生成与控制策略，通过正向运动学和逆运动学建模分析得到了系统的闭环传递函数，并分别对微铣平移轴和旋转工作台的转动轴进行控制策略研究，最后通过仿真与实验验证了本文提出方法的有效性，微铣轴的跟踪误差在10μm以内，旋转工作台的直线运动的误差为1μm，旋转误差为20μrad，本文所提出的轨迹生成策略可以在不损失任何运动轴的情况下处理运动冗余，同时设计理念，运动学和控制方法可以应用在新型的微机床上，下一步需要研究提高带宽和轨迹生成精度下，逐渐减小微铣力的影响。

[参考文献]

[1] 王伟, 陶文坚, 李晴朝. 五轴数控机床动态精度检验试件特性研究[J]. 机械工程学报, 2017, 53(1): 101-109.

[2] Zhang J, Zhang L, Zhang K, et al. Double NURBS trajectory generation and synchronous interpolation for five-axis machining based on dual quaternion algorithm[J]. The International Journal of Advanced Manufacturing Technology, 2016, 83(9-12): 2015-2025.

[3] 唐清春, 黎国强, 刘谦, 等. 摆头转台五轴数控机床 RTCP 算法的研究[J]. 组合机床与自动化加工技术, 2016 (5): 39-42.

[4] Sun C, Altintas Y. Chatter free tool orientations in 5-axis ball-end milling[J]. International Journal of Machine Tools and Manufacture, 2016, 106: 89-97.

[5] Takeuchi Y, Sakaida Y, Sawada K, et al. Development of a 5-axis control ultraprecision milling machine for micromachining based on non-friction servomechanisms[J]. CIRP Annals-Manufacturing Technology, 2000, 49(1): 295-298.

[6] Lu X. 6D direct-drive technology for planar motion stages[J]. CIRP Annals-Manufacturing Technology, 2012, 61(1): 359-362.

[7] 魏兆成, 王敏杰, 王学文, 等. 球头铣刀曲面多轴加工的刀具接触区半解析建模[J]. 机械工程学报, 2017, 53(1): 198-205.

[8] 廉良冲, 伍浩, 刘国栋, 等. 高精度 U 形薄壁铝支座零件多轴数控加工工艺改进[J]. 机床与液压, 2016, 44(20): 67-69.

[9] Choi Y M, Gweon D G. A high-precision dual-servo stage using Halbach linear active magnetic bearings[J]. IEEE/ASME Transactions on Mechatronics, 2011, 16(5): 925-931.

[10] 王雷, 李明, 唐敦兵, 等. 基于改进遗传算法的机器人动态路径规划[J]. 南京航空航天大学学报, 2016, 48(6): 841-846.

[11] 陈琳, 韦志琪, 徐杰, 等. 基于 CAD 的机器人表面制造工具轨迹规划方法[J]. 组合机床与自动化加工技术, 2017 (2): 1-4.

[12] 李聪聪, 郝敬宾, 陈鑫, 等. 基于 3+2 轴加工平台激光熔覆的路径生成优化[J]. 制造技术与机床, 2016 (9): 107-111.

[13] 刘庆龙, 张进生, 高伟, 等. 新型石板材上下料装置的结构设计与轨迹规划[J]. 组合机床与自动化加工技术, 2016 (11): 46-49.

[14] 吴雁, 阮胜, 郑刚, 等. 基于侧铣刀位生成复杂曲面在机测量路径研究[J]. 机械设计与制造, 2016 (11): 187-189.