直线负载模拟器及其新型CMAC改进算法控制

徐志伟，范元勋，汪训浪，雷建杰，戴 立

(南京理工大学 a.机械工程学院；b.自动化学院，南京 210094)

0 引言

为保证姿/轨控动力发动机的动态控制性能，要求其燃气阀具有快速响应性能，而传统的燃气电磁阀因较强的电磁惯性及响应明显滞后等缺点很难达到快速响应，故一种新型的电动直线阀逐渐取代电磁阀。直线负载模拟器用于模拟此电动直线阀在实际工况下的真实负载。历年来研究重点多集中于多余力矩抑制方面，但对负载模拟器的研究多应用于对旋转舵机的加载测试，即多集中于扭转对扭转的扭矩式加载，而直线式负载模拟器结构较为复杂，且主动直线运动所导致的多余力更难抑制[1]。

当前，利用智能控制算法来代替传统控制方法成为当前多余力(矩)抑制的热点，而CMAC(Cerebellar Model Articulation Controller)即小脑模型神经网络，其结构简单，学习速度快，适应于被动式负载模拟器的实时控制[2]。文献[2]针对无人机舵机的负载模拟器，引入了非均匀量化方法，并利用高斯权重常数来分配CMAC误差，仿真表明，所提算法将多余力矩的干扰降低到了3.5%；文献[3]采用CMAC和PD结合的控制方法，并引入自适应学习率，仿真运行超60s后系统仍然稳定，但其应用对象仅为单输入单输出系统；文献[4]提出一种新的CMAC权值更新公式，新的CMAC算法旨在提高负载模拟器输出平滑性，把稳态误差降低了21%，并进行实物实验验证了其可行性；文献[5]提出了一种模糊与CMAC复合的FCMAC方法，用于对永磁直线电机的逆控制，并实现了复杂逆模型简单化。

在借鉴文献[2-5]的基础上，为对某型航天用电动直线阀进行性能加载测试，设计了一种直线负载模拟器(Linear Loading Simulator, LLS)；提出了一种基于CMAC前馈控制和PD(Proportional Derivative,PD)反馈控制的新型CMAC改进算法；提出一种二维非均匀量化方法，并引入量化距离的概念，在两维度上来计算高斯权重，并提出一种抑制CMAC过学习现象的新型权重计算方法。仿真及实验表明，基于新型CMAC的复合控制方法在LLS中取得了较好的效果，通过自主研发的LLS验证了其有效性。

1 直线负载模拟器原理与建模

LLS由加载系统与承载系统相互耦合组成，如图1所示。加载系统采用面贴式永磁同步电机(PMSM)为加载动力输出，并应用高精度滚珠丝杠副对电动直线阀进行直线加载；拉压力传感器与电动直线阀通过螺纹连接节连接，并可将测得加载力反馈给实时控制器进行闭环控制；转矩转速传感器可测得LLS输出转矩、转速信号并反馈给实时控制器。

图1 LLS原理结构图

LLS数学模型由直线负载模拟机理模型和被测电动直线阀机理模型组成；其中，负载模拟机理模型主要考虑驱动元件PMSM模型与滚珠丝杠副转换模型。在理想情况下[6]，PMSM的电压平衡方程为：

(1)

式中，uq、iq分别为PMSM定子在q轴上的电压和电流；Lm为等效电感；Rm为定子绕组电阻；Ke为反电动势常数；ωm为PMSM转子角速度。

PMSM转矩平衡方程为：

(2)

式中，Tm为PMSM电磁转矩；Jm为PMSM转动惯量；Bm为PMSM阻尼系数；TL为PMSM输出转矩。

负载模拟器的PMSM扭矩输出需经联轴器、转矩转速、传感器及滚珠丝杠副传递输出给电动直线阀，将此中间元件视为LLS系统负载，故PMSM输出转矩TL视为由惯性负载、阻尼负载及弹性负载组成，其平衡方程为[7]：

(3)

式中,JL为负载转动惯量；BL为负载等效阻尼系数；KL为负载等效弹性刚度系数；θL为滚珠丝杠角位移；θm为PMSM角位移。

由滚珠丝杠模型[8]，得负载模拟输出力F与PMSM输出转矩TL的方程、负载模拟输出位移L1与滚珠丝杠角位移θL的方程：

(4)

式中,F为负载模拟输出力；r为滚珠丝杠副半径；λ为丝杠螺纹升角；L1为负载模拟输出位移；P为丝杠导程。

电动直线阀应用一种高减速比的间接驱动方法，此方法中直流力矩电机(DC Torque Motor, DCTM)为驱动电机，电机输出经减速器、精密滚珠丝杠实现位移控制；其中，电动直线阀输入电压u1和输出位移L1关系方程：

(5)

式中，Kdm为DCTM电磁转矩系数；Kd0为DCTM功放系数；kj为直线阀的减速比；P1为直线阀中滚珠丝杠导程；Kde为DCTM反电势系数；Rd为DCTM电阻；Ld为DCTM电感；Jd为DCTM转动惯量；Bd为阻尼系数。

综合式(1)～式(5)，求得LLS传递函数如式(6)所示，式(6)、式(7)中Kt为PMSM电磁转矩系数。当电动直线阀输入电压u1=0时，式(6)中uq的系数表征的是LLS的前向通道特性；当PMSM输入电压uq=0时，式(6)中u1的系数表征的是LLS的扰动通道特性。

(6)

其中，

G4={(Lms+Rm)[(Jm+JL)s2+(Bm+BL)s+
KL]+KtKes}rtanλ

(7)

2 新型CMAC改进控制方法

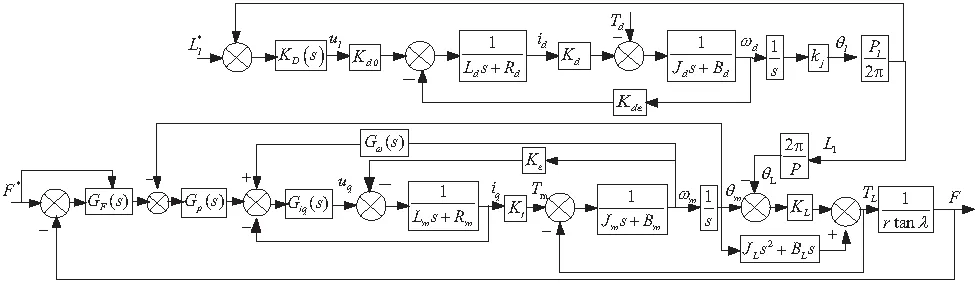
图2 LLS控制框图

图3 新型CMAC复合控制原理

CMAC-PD复合控制是指CMAC作为前馈控制，以保证LLS响应速度；PD控制器作为反馈控制，在CMAC训练初期实现固定增益控制以确保LLS系统稳定。而常规CMAC控制仅均匀量化一维输入信号，且网络训练完成后，CMAC所产生的累积误差会导致过学习现象，进而可能导致输出发散，影响LLS系统稳定性[10]。为解决传统CMAC-PD过学习现象，在文献[2-4,9,12]的基础上，提出一种针对LLS力外环GF(s)的新型CMAC改进算法，引入了非均匀量化与量化距离的概念，其控制算法如下：

(1)非均匀量化：以LLS指令力F*与输出力F作为新型CMAC的二维输入信号，并利用图4所示曲线，按照设定非均匀量化率μ，对二维空间节点进行非均匀量化，得每一维输入的量化向量；图4中，簇心由输入向量概率密度函数的极大值来确定，且越靠近簇心，量化点越集中；其中：

若第m个量化点在中心左侧(m≤[Ni/2])，则：

step=2(Oi-Ai)/Ni

(8)

Pi=Ai+(m-0.5)·step

(9)

Qi,m=Ai+(Oi-Ai)ln(1+μ|Ai-Pi|/Oi-Ai)

(10)

式中，Ni为第i维输入向量的量化点数；step为采样步距；Pi为此量化点的位置；Qi,m为二维激励信号的量化值；Oi为量化中心；Ai为左边界；μ值表示非均匀程度；

若第m个量化点在中心右侧(m>[Ni/2])，则：

step=2(Bi-Oi)/Ni

(11)

Pi=Oi+(m-[Ni/2]-0.5)·step

(12)

Qi,m=Bi-(Bi-Oi)ln(1+μ|Pi-Bi|/Bi-Oi)

(13)

式中，Bi为左边界。

图4 非均匀量化分布曲线

(2)引入量化距离，由量化距离求二维新型CMAC的激活区域；其中，量化距离由高斯函数所表征，再利用二维输入向量中各维采样点与其对应量化点间的距离，求得量化点的量化距离值，则第i维第m个激励信号的量化距离向量Di,m可表示为：

(14)

式中，i=1,2；m=1,2,…,Ni；gi为第i维输入信号；w为高斯函数宽度系数。

向量Di,m取值在区间[0,1]之间，由预设门限值判定激活区域的范围，Di,m超过在门限值，则此量化点为被激活，反之则为休眠；。

(3)计算概念空间权值Gsi，利用步骤 (2)中所求的量化距离值Di,m计算每个概念空间中激活的量化点所对应的高斯权重为：

(15)

(4)计算物理空间权值Gpi，采用压缩映射法将步骤(3)中高斯权重Gsj压缩映射到节点数目更少的物理空间，得物理空间权值第i个高斯权重Gpi：

Gpi=GsjmodNp

(16)

式中，i=1,2,…,Np;j=1,2,…,M；Np表示物理存储空间大小；M代表虚拟联想空间大小。

(17)

(6)采用梯度下降法对CMAC网络权值进行学习修正，步骤(5)中所提力外环GF(s)输出U为：

U=Ys+YP

(18)

式中，YP为PD控制器输出；为协调系统快速稳定性与CMAC过学习现象之间的矛盾，利用系统的跟踪误差信号E来进行调整权值，权值规则改为：

(19)

式中，β为平衡常数，可根据系统模型实际取值，用来平衡调节系统稳定性和收敛速度；η为0～1之间的常数，而η(1-e-β|E|)代替常规CMAC算法中的固定学习率η，由其表达式可看出，当跟踪误差E较小时，较小的改进后学习率能够抑制系统的误差累积，故可解决系统的不稳定性问题；而当跟踪误差E较大时，较大的改进后学习率可提高系统的收敛速度[11]。因此，改进后的CMAC算法能够显著地抑制传统CMAC累积误差对系统稳定性造成的影响。

3 仿真与实验

为验证所提新型CMAC改进算法是否对某型自研直线负载模拟器有效，在实验之前，须先对所提方法与常规PID控制、常规一维CMAC-PD控制进行对比仿真分析；所提对比策略仅依次用于力外环GF(s)控制器中，其他控制器参数相同。另外，LLS主要参数见表1。

表1 系统参数表

其中，Giq(s)的参数设定为：KCP=4.1，KCI=450，开环截止频率KCω=1000；Gp(s)的参数设定为：P1=1.32，I1=0.61，D1=0.02；在基于新型CMAC改进算法控制的力外环控制器GF(s)中，PD控制器参数为：KP=2.3，KD=0.09；新型CMAC参数为：量化级数N1=N2=100，非均匀程度μ=1.3，激活区域预设门限区间为[0.935,1]，高斯函数宽度系数w=10，学习率η=0.2。

3.1 复合控制跟踪稳定性仿真

下面针对所提新型CMAC改进算法与常规PID控制、传统一维CMAC-PD算法进行对比分析，其中与之对比的传统一维CMAC-PD算法参数设定为：量化级数R=100，泛化常数C=100，学习率μ=0.2；PD控制器参数为：KP=2.3，KD=0.09。

CMAC-PD复合控制中可能出现“过学习”现象使得系统发散，有必要测试所提新型CMAC算法的稳定性。信号设定同上，仿真时间取100 s。如图6所示，可见新型CMAC算法能够使误差信号快速收敛，在经过100 s后误差基本保持在160 N左右，并没有呈现处发散的趋势；结果表明，采用二维非均匀量化的CMAC控制有效地提高了LLS加载精度，抑制了过学习现象。

图5 LLS正弦信号误差跟踪曲线

图6 新型CMAC复合控制误差

3.2 正弦跟踪实验

基于所设计直线负载模拟器(LLS)及所提新型CMAC改进算法的有效性，在自行研制的LLS试验台上进行正弦跟踪试验，信号设定同上，图7为试验台实物照片，图8为正弦跟踪结果。

1.PMSM 2.转矩转速传感器 3.滚珠丝杠副 4.拉压力传感器 5.电动直线阀图7 LLS试验台实物照片

图8中，虽然一开始加载力反馈值正峰值达2288.07 N，且加载力跟踪曲线有明显-6.52°的相位滞后，但经过不到1 s时间能够快速追踪指令信号，输出力与指令力曲线基本重合，误差基本稳定在160 N左右，表明所提策略有效地提高了LLS的加载精度，并提高了LLS的稳定性。工程上常用指令力矩与实际输出力矩间的相位差与幅值差来衡量负载模拟器性能，当反馈信号幅值误差小于±10%和相位误差变化小于10°时，即称之为“双十指标”[12]。由此可见，所提控制方法使LLS加载精度达到理想的“双十指标”。

图8 基于改进CMAC控制的LLS跟踪曲线

4 结论

直线负载模拟器(LLS)有效地测试了在电动直线阀在输出2 mm位移的同时能够承受2000 N的外载；为提高LLS加载力精度，抑制直线阀多余力干扰，建立LLS与直线阀耦合模型并分析其通道特性。而针对LLS典型非线性系统，提出一种基于二维高斯权值非均匀量化的新型CMAC改进算法，采用LLS指令值与反馈值作为CMAC的二维激励信号，并改进了CMAC网络权值的学习方法。结果表明，该方法能够动态调整CMAC泛化性能，在保证其输出平滑性的同时又能抑制其误差积累所导致的发散问题，有效抑制了直线阀所带来72.69%的多余力，基于新型CMAC的复合控制使得直线加载跟踪精度达到92.33%，达到了工程实现所要求的“双十指标”。

[参考文献]

[1] Wang Chengwen, Jiao Zongxia, Wu Shuai,et al. An experimental study of the dual-loop control of electro-hydraulic load simulator(EHLS)[J]. Chinese Journal of Aeronautics, 2013, 26(6): 1586-1595.

[2] 杨波, 王哲. 新型小脑模型关联控制器复合控制在电动加载系统中的结构及算法[J]. 控制理论与应用, 2011, 28(6): 827-833.

[3] 杨波, 王俊奎. 无人机舵面负载模拟系统的小脑模型控制[J]. 北京航空航天大学学报, 2009, 35(11): 1361-1365.

[4] 杨波, 程龙. 提高电动加载系统输出平滑的CMAC复合控制[J]. 北京航空航天大学学报, 2013, 39(6): 723-727.

[5] 孙宜标, 郭庆鼎, 赵希梅. 基于模糊小脑模型神经网络的直线伺服跟踪控制研究[J]. 组合机床与自动化加工技术, 2008(8): 50-54.

[6] 王哲. 被动式力矩伺服系统加载策略研究[D]. 哈尔滨:哈尔滨工业大学, 2015.

[7] Sebastian Abu. Design methodologies fot robust nano-positioning[J]. IEEE Transactions on Control Systems Technology,2005: 868-876.

[8] 濮建荣. 行星滚柱丝杠副接触、摩擦与工作特性的理论与试验研究[D]. 南京:南京理工大学, 2015.

[9] 杨波, 王俊奎. 基于改进的CMAC的电动加载系统复合控制[J]. 航空学报, 2008, 29(5):1314-1318.

[10] Su Sh F, Tao T, Hung T H. Credit assigned CMAC and its application to online learning robust controllers[J]. IEEE Transactions on System, Man and Cybemetics, Part B, 2003, 33(2): 202-213.

[11] 王刚, 李建府, 朱荣刚. CMAC改进算法在电动负载模拟器的应用[J]. 电光与控制, 2011, 18(4): 72-76.

[12] 焦宗夏, 华清, 王晓东. 负载模拟器的评价指标体系[J]. 机械工程学报, 2002, 38(11):26-30.