基于支持向量机的远程磨加工报警系统的研究*

职占新，郑 鹏

(郑州大学 机械工程学院，郑州 450001)

0 引言

随着现代制造业的发展，对精密零件的加工质量的要求越来越高。磨削加工是精密零件的重要加工环节，因此提升磨削加工过程的控制与检测的自动化程度，对精密零件的加工质量有着重要的影响[5]。目前，国内外众多研究机构已经展开了利用机器学习的方法对零件磨削加工过程的控制与检测进行研究。例如利用神经网络算法对零件表面粗糙度和圆度进行预测。但大多研究还仅仅停留在理论，并没有应用在实际加工中。

针对磨削加工中对加工尺寸误差超出预设值范围时报警的需求，设计了基于支持向量机的远程磨加工报警系统。该系统的尺寸预测是通过支持向量机利用已有加工参数对加工工件尺寸提前做出预测，并将预测尺寸与工件的加工尺寸比较，若工件尺寸预测尺寸超出预设值范围，则报警系统发出报警提示。防止由于进给速度不均匀而影响工件的磨削质量或导致工件最终加工尺寸受到影响。

1 磨加工远程报警系统

磨床的加工信息由监控节点上传到工程节点并且显示在客户端的监控界面，实现了远程监控的目的。用户方便快捷的获得磨床加工数据，明显提升了监控与管理的效率。报警系统的基本架构是利用组态软件的几个基本组成部分的相互联系，实现磨床零件加工过程的实时监控。

系统的主要框架包括三大部分：

(1)监控节点(SCADA node)

(2)工程节点(Project node)

工程节点是软件的开发平台，可构建图形、配置I/O、下载文件，还可以通过编写程序来处理从监控节点得来的数据。

(3)客户端(Client)

客户端通过内部或者外部网可以查看监控画面，并且具有确认警报和修改点值的权限。

系统网络框架如图1所示。监控节点进行数据的采集，工程节点将支持向量机的算法加入系统，建立模型对工件尺寸进行预测[1]。

图1 系统的网络架构图

现场传感器采集磨床的加工信息，把信息传送到系统相应的监控节点，监控节点再把信息上传到工程节点，由工程节点进行加工处理，最终显示在监控界面上[4]。

2 支持向量机及预测模型

2.1 支持向量机

支持向量机是一种基于统计理论的机器学习方法，它的特点是在尽量保证训练样本的准确前提下，提升模型的通用性，广泛的应用于理论分析和工程研究上[3]。

许多医院更多的是重视医疗卫生技术的提升，尽管对于市场经济来说，医疗卫生技术确实是医院的核心竞争力，但是在医院核心竞争力没有太大的差别时，就需要通过内部控制来提升软实力。但是有些医院尽管构建了内部控制机制，但是并没有严格根据其制度进行落实，多数都是将其作为一种流程，甚至作为一种摆设，并没有将其视为制度进行严格落实。而且因为医院缺乏对于内部控制的评价以及有效的监督，主要就是由于医院更加注重临床管理水平与技术的发展，同时在医疗设备及聘用临床医务人员的投入较多，因此在构建内部控制监督体系就尽可能的降低投入，缺乏监督自然就不会有人将其进行严格的落实。

分类函数的描述可以定义如下：

f(x)=wTx+b

(1)

其中，x,wT均为n维向量。

对于分类函数来说，几何间隔：

γ=yi(wTx+b)/w

(2)

γ越大，分类的准确度越高，yi为分类类别。引入拉格朗日对偶变量α。

(3)

α是拉格朗日对偶变量。通过SMO算法将α求解出来，便能将w,b求解出来。即通过引入拉格朗日变量，通过计算对偶变量α可得到最优w,b。

上述算式在线性可分的情况下可以直接得到w,b，如果线性不可分，常常需要将数据映射到高维。如果用常规方法将向量映射到高维空间中，在维数逼近无数维时，计算量十分庞大，计算机无法处理。支持向量机引入核函数后，数据在低维空间中即可进行得到高维映射结果，不需要展开到高维。核函数的出现优化了计算的复杂度，削减了运算量。支持向量模型变为：

(4)

通常会从一些常用的核函数中做出选择，本文采用的是RBF核函数：

K(xi,xj)=exp(-(xi-xj)2/(2σ2))=exp(-(xi-xj)2/g)

(5)

式中，g=1/(2σ2)为核参数。

2.2 参数寻优

在支持向量机算法中，采用不同的参数，会得到不同的支持向量机预测模型，最终数据处理的结果也不相同。因此优化参数的方法值得我们去研究。常用的对预测模型参数寻优方法有网格法，遗传算法，交叉验证方法等。

本文主要通过交叉验证的方法来优化核参数g和惩罚参数c，经过交叉验证优化后可有效的避免预测模型过学习与欠学习情况发生，使模型的泛化能力提升。

交叉验证经常采用K-fold CV方法，将数据分为K份。其中的K-1组数据用来训练模型，剩下的一组用来验证模型的优劣。每一组都参与验证模型的优劣，可以得到K组模型，将K个模型的准确率作算数平均值，作为K-fold CV的评价指标。因为采用交叉验证的方法每组数据都要参与训练模型和验证模型，避免了由于分组的不确定性而产生的误差。图2为计算机模拟交叉验证的过程。其中x,y坐标轴分别代表不同的log以2为底的c,g，z坐标表示准确率。其中颜色越红代表准确率越高。

在准确率相同的条件下，优先选择惩罚参数小的那组作为模型的参数，这样可以使模型的泛化能力更强。

图2 交叉验证的参数分布图

2.3 支持向量机算法预测模型

通过分析磨床加工时尺寸数据，将磨床进给时的尺寸变化数据与磨加工工艺参数作为训练集。根据训练集建立预测模型，根据预测模型预测下一时段的磨削尺寸。并且将实时阶段的预测尺寸与实际尺寸作对比，若实时预测尺寸在预设值范围内，将实时预测尺寸加入训练集，重新确定实际模型，具体步骤如下。

(1)对磨加工中的工件反复试验，通过改变磨削加工进给速度来获得不同的尺寸改变速度。加工完成后将工件进行相关计算，最终得到工件的尺寸变化数据。

(2)选定训练集与测试集，首先对训练集与测试集做预处理，剔除数据集中的粗大误差。对数据集做归一化处理，归一函数如下：

f:x→y=(x-xmin)/xmax-xmin

(6)

归一函数的作用是将数据映射到[0,1]内，避免因为x,y本身数据值过大而忽略较小的变化。除了将数据归一到[0,1]，还可以将数据归一到[-1,1]，函数如下：

f:x→y=2(x-xmin)/xmax-xmin+(-1)

(7)

(3)通过训练集建立支持向量机回归模型，并且通过交叉验证得到最优惩罚参数c与核参数g。通过模型预测的尺寸与实际尺寸作对比，若误差在预设值范围内，证明模型可行。预测模型框图如图3所示。

图3 预测模型框图

3 实验

实验采用外圆磨削的方式，选用的磨床型号为MGB1320E高精度半自动外圆磨床。采用GYSyn 256C磨削液，砂轮材质为棕刚玉，直径400mm,厚度32mm，最高线速度35m/s，如图4所示。

图4 磨削实验设备

在磨加工时尽量避免接触工件，减小由于人为因素对尺寸造成的误差。每隔一个单位时间测量记录一组数据，共记录20组数据，如表1所示。前10组预测值与实际测量值如图5所示(单位mm)。通过多组测试数据建立出尺寸预测模型，通过交叉验证参数寻优后得到最优参数(c=2.11,g=2.58)。

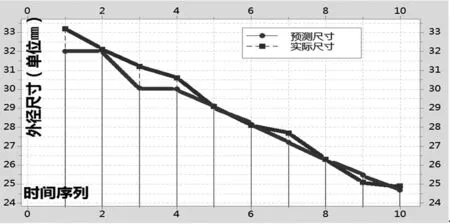
图5 外径尺寸预测值与实测值对比图

序号12345678910测量值mm预测值mm33.232.0132.132.0531.230.0730.630.0229.129.1328.128.1627.727.2026.326.3125.125.4824.924.69序号11121314151617181920测量值mm预测值mm24.223.9023.123.0921.922.2621.121.420.720.7320.220.1319.719.6919.319.4518.918.6518.418.69

图6 报警画面

从实验数据可得，预测值与实测值的最大误差不超过2mm，小于给定的系统误差预设值范围，均方误差为MRE=0.0070,MSE=0.0020，均方根误差越小证明预测结果越可靠。实验的结果证明该支持向量机模型可行。若实时测量值与预测值之间的差值超过系统误差预设值时，通过监控节点将信息上传到工程节点，由工程节点进行加工处理。最终显示在监控界面上显示报警信息，报警画面如图6所示，提示加工存在问题。防止由于进给速度不均匀影响工件的磨削质量或导致工件最终加工尺寸受到影响。

4 结论

针对磨削加工中的报警的需求，提出了一种基于支持向量机的磨加工报警系统。通过实验分析，验证了将支持向量机模型嵌入的报警系统中，对尺寸预测值精度满足实际应用。通过监测预测值和实测值的误差，实现了用户对于报警的需求。并能及时将加工过程中加工信息反馈，实时调节尺寸序列，降低了预测误差，降低了磨削废品率。提升了磨削精度的同时也提升了磨削自动化水平,有值得推广的价值。

[参考文献]

[1] 高方.磨加工主动测量控制的关键技术及应用[D].郑州:郑州大学,2014.

[2] 宁会峰.珩磨加工中在线气动测量与尺寸控制技术研究[D].兰州：兰州理工大学,2012.

[3] 任冠青,张琳娜，郑鹏.WinCE多线程在磨加工主动量仪控制系统中的应用[J].组合机床与自动化加工技术,2013(8):77-79.

[4] 陈六三,张兴权,汪世益,等. CBN砂轮磨削深度对渗碳淬火钢表面质量的影响[J]. 金属热处理,2013(6):89-92.

[5] 李国发,王龙山,丁宁. 基于进化神经网络外圆纵向磨削表面粗糙度的在线预测[J]. 中国机械工程,2005,16(3):223-226.

[6] 王家忠,王龙山,周桂红,等. 基于模糊基函数网络和自适应最小二乘算法的外圆纵向磨削表面粗糙度的预测[J]. 中国机械工程,2006,17(12):1223-1227.

[7] 牛家洋.基于神经网络的非线性系统时间序列的预测方法研究[D].济南:山东师范大学,2013.

[8] 崔立志.灰色预测技术及其应用研究[D].南京:南京航空航天大学,2010.

[9] 向昌盛.基于支持向量机的时间序列组合预测模型[D].长沙:湖南农业大学,2011.

[10] 向红军,雷彬.基于单片机系统的数字滤波方法的研究[J].电测与仪表,2005(9):53-55.