多项式加减速的NURBS插补控制方法*

李英祺 ，王桂荣

(中国计量大学 机电工程学院，杭州 310018)

0 引言

参数曲线插补是实现高速高精度数控加工的重要方法，解决了传统加工方法在复杂零件加工方面的缺陷[1]。在所有参数曲线模型中，NURBS曲线可提供通用数学表达式且具有良好的性质而被广泛应用[2]。

在NURBS曲线中高曲率区域与平滑区域频繁变化，进给速度的规划决定了速度加速或减速的位置。文献[3]在速度自适应控制中将曲线中点和弦长中点之间距离近似弓高误差，但在曲线拐点处误差较大。文献[4]提出根据弓高误差限制可自适应调整进给速度，但忽略了机床自身的加减速性能。上述文献实现了对进给速度进行自动调节但忽略在NURBS曲线插补全程中的加减速处理。文献[5-7]利用S曲线加减速控制方法对NURBS曲线进行全程插补处理，保证了加速度的平稳变化，但加加速度的变化是跳跃式的，这种跳跃会引起机床运动时的震颤，不能满足一些细小的、对零件加工过于严谨的要求。针对S曲线加减速控制方法存在的问题，文献[8-10]提出多项式加减速方法运用于NURBS曲线插补中，可保证系统有较高的柔性，但构造的多项式加减速曲线S(t)、V(t)、A(t)、J(t)等计算公式分段多且计算复杂，用于实际插补中会使得插补周期变长影响加工效率。

基于对上述文献的研究，本文提出一种新的多项式5段加减速的NURBS曲线插补控制方法，对NURBS曲线全过程进行速度规划的自适应分段插补。满足对进给速度、加速度、加加速度的控制要求，满足机床各种限制约束，通过仿真实验验证了所提方法的优越性。

1 NURBS曲线基本概念

1.1 NURBS曲线的定义

一条p次NURBS曲线的表达式[2]如下:

(1)

由cox-de Boor递推公式可以求出p次Ni,p(u)：

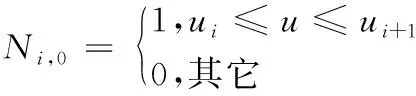
(2)

1.2 NURBS曲线长度的求取算法

在NURBS曲线插补前，必须先已知弧长才可以加减速速度规划。从点C(u1)到点C(u2)的曲线长度L可表示为：

(3)

由式(1)、式(2)可求出各节点区间上的参数坐标(x(u),y(u))，因一般难得到计算NURBS曲线弧长被积函数的原函数，故利用数值积分求曲线长度。辛普森自适应积分方法[11]可根据被积函数在积分区间上的变化快慢自适应细分区间，所以利用该方法求取曲线长度。通过在Matlab中设计递归程序来实现辛普森自适应方法。

2 NURBS曲线插补算法

2.1 自适应速度控制

在实际运动过程中，通过微小直线段来代替NURBS曲线段，插补参数点仍然在NURBS曲线上，并没有产生径向误差但是引入弓高误差。弓高误差δ与进给步长ΔL、曲率半径ρ有关，为满足加工精度要求必须把弓高误差限制在一定范围内。因此在最大弓高误差δmax限制下的进给步长为：

(4)

在速度较大、曲线曲率较大时，轨迹向心加速度过大会导致轨迹精度降低，且对机床系统产生较大的冲击，最大向心加速度必须限制在合理的范围内。因此在最大向心加速度限制下的进给步长为：

(5)

在一个插补周期内，结合给定速度求得进给步长值为ΔL3=viΔT，由此可得在周期内的速度v=min{ΔL1/ΔT,ΔL2/ΔT,ΔL3/ΔT}。

2.2 分段预处理与插补计算过程

如图1所示为NURBS插补曲线轨迹。经过自适应速度控制后得到NURBS曲线的各项数据，找出对应分段点，分段后进行分段预处理。具体步骤如下：

步骤1：参数ui从0开始计算得到当前插补点C(ui)坐标，根据2.1节中得出满足曲线精度要的进给速度v(ui)，利用2阶Taylor展开式来计算下个周期参数值ui+1，即

也有不针对具体人的、目的不明确的签文：比如说把一块锡兰岛的蓝宝石扔进幼发拉底河，在塔顶放飞一只鸟，每一百年在沙粒无数的海滩上取走（或加上）一粒沙等等。有时候，这类签的后果十分可怕。

(6)

步骤2：根据2.1节中最大弓高误差和最大向心加速度的约束，找出曲线曲率极大值点位置并在此处作为分段点，如图2a为Ku1、Ku2、Ku3、Ku4为各曲率极大值点，图2b为自适应速度控制插后的进给速度图；

步骤3：如图1所示：在曲率极大值Ku1、Ku2、Ku3、Ku4处作为分段点，确定各分段点处的参数ui值，将曲线分成Lu0u1、Lu1u2、Lu2u3、Lu3u4、Lu4u0这5段利用1.2节的方法求出各分段曲线的长度Li。计算出各段的最大速度值为vmax、起始速度值为vs、终点速度值为ve，在各分段曲线进行多项式加减速规划。如表1所示为各分段点及其各分段长度。

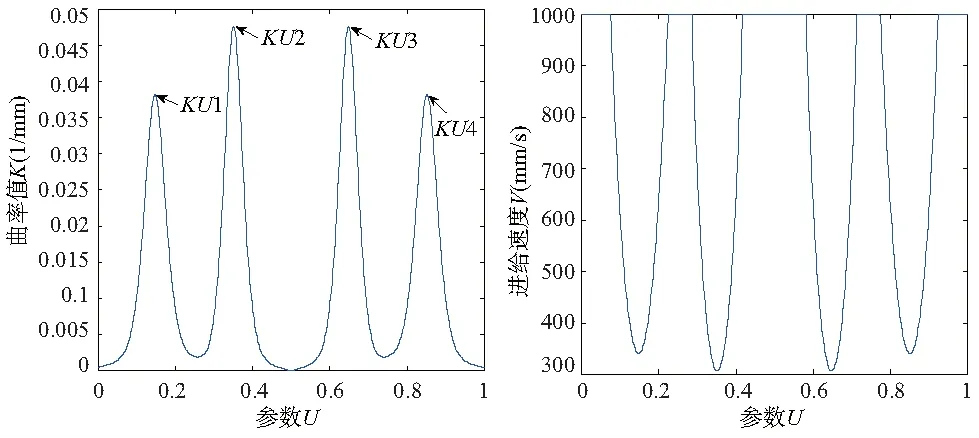
(a) 自适应速度控制后的曲线曲率 (b)自适应速度控制后的进给速度图2 自适应速度控制曲线

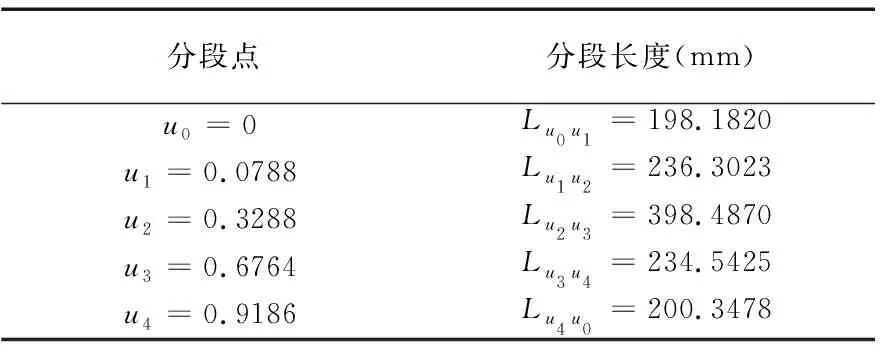
分段点分段长度(mm)u0=0Lu0u1=198.1820u1=0.0788Lu1u2=236.3023u2=0.3288Lu2u3=398.4870u3=0.6764Lu3u4=234.5425u4=0.9186Lu4u0=200.3478

3 多项式5段加减速的NURBS控制方法

3.1 多项式5段加减速计算模型

多项式5段加减速控制方法可实现全过程中加加速度的连续变化，有效解决机床的冲击和振动问题。图3为构造的多项式5段加减速全过程，加加速度可设计为三角形的变化规律，整个过程可以分为以下5个阶段：加加速段(T1和T2)、减加速段(T3和T4)、匀速段T5、加减速段(T6和T7)、减减速段(T8和T9)。其中T1=T2=T3=T4，T6=T7=T8=T9，vc为进给速度，起始速度vs，终点速度ve，τi=t-ti-1表示各个阶段的起始点作为起点的时间，Ti为各阶段持续运行时间，k为三角形斜率。

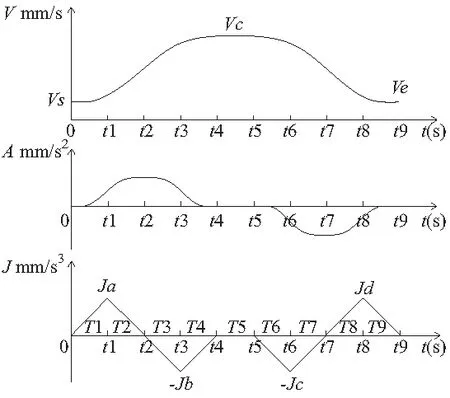
图3 多项式5段的过程曲线图

(7)

(8)

(9)

(10)

其中，

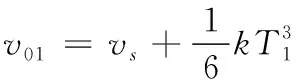
上述为多项式5段加减速控制方法的基本公式，由式(7)～式(10)可知，只要确定了T1、T5、T6就可以构造出多项式5段加减速控制曲线，求得各时刻所对应的J(t)、A(t)、V(t)、S(t)等就可以判断处加减速阶段。

3.2 多项式5段加减速控制算法

在实际运用中，多项式5段运行过程中并不是总包含完整的5个过程，必须根据起始速度vs、终点速度ve、进给速度vc、待插补曲线长度S来确定实际运行情况。当待插补曲线足够长，实际速度可以到达vc值；而长度较短时，实际速度到达小于vc的某一值。

(1)实际速度可达到进给速度的情况

(11)

由式(11)可求出时间T1，如式(12)所示：

(12)

同理，时间T6如式(13)所示：

(13)

将T1和T6代入式(10)中分别求出La、Ld，可得：

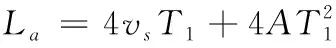
(14)

因此，匀速运行时间为式(15)：

(15)

即求出T1、T5、T6后，可构造出完整的V(t)、A(t)、J(t)曲线图。

(2)实际速度不可达到进给速度的情况

当S≤La+Ld，表示曲线长度太短则需重新进行速度规划。此时未达到给定进给速度vc，不存在匀速段，则T5=0。根据式(16)通过Matlab编程求出最大速度vmax。

(16)

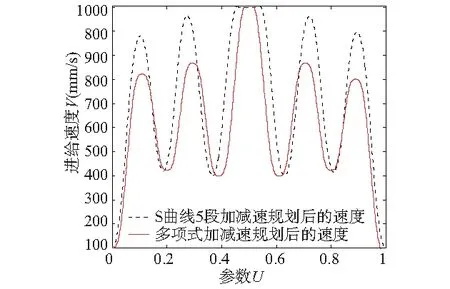
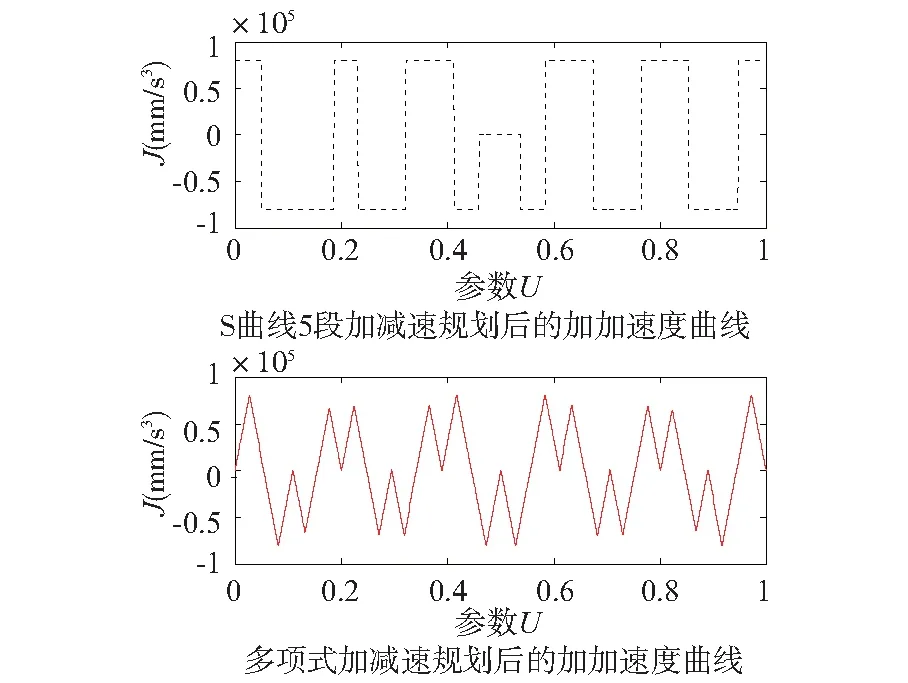
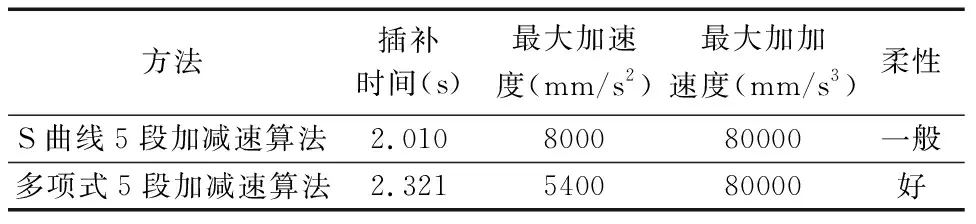
当S=La(vs

得出各阶段运行时间后，就可以由式(7)～式(10)构造出完整的加加速度、加速度、速度曲线。各段NURBS曲线按照重新规划好的多项式加减速方案完成插补过程。

4 NURBS曲线仿真分析与结果

以一段待加工NURBS曲线为例，验证所提方法的有效性和正确性，利用多项式5段加减速和S曲线5段加减速这两种方法进行对比。图1为待插补的NURBS曲线，参数值设定如下:曲线次数为p=3，节点矢量为U=[0 0 0 0 0.25 0.5 0.75 1 1 1 1]，权因子为W=[1 2 2 1 2 2 1]，控制定点为d=[(0 0);(-200 -200);(-200 200); (0 0); (200 200);(0 0)]。

在Matlab中进行仿真，参数值设定如下：插补周期为Ts=0.001s，vs=0mm/s ，ve=0mm/s，vc=1000mm/s，最大加加速度为Jmax=80000mm/s3，最大加速度为Amax=8000mm/s2，机床所允许的最大向心加速度为amax=6000mm/s2，最大弓高误差为5×10-4mm，斜率k=1.2×106mm/s4。

在相同插补周期内，对S曲线5段加减速分段规划和多项式5段加减速分段规划这2种方法进行插补加工。如图4a为自适应速度控制后的弓高误差图，误差值在5×10-4mm内；图4b是运用两种方法后获得的弓高误差曲线比较图，S曲线5段加减速方法规划后得到的弓高误差与多项式5段加减速规划后得到的弓高误差曲线基本重合，表明这两种方法的加工精度明显优于自适应速度控制插补方法。

(a) 自适应速度控制后的弓高误差 (b) 两种方法的弓高误差比较图图4 弓高误差

如图2所示为自适应速度控制方法下的进给速度图，除了在曲率极大值附近速度会降低外在其他位置的速度都能达到1000mm/s，整段曲线平均速度为739.55mm/s。如图5所示，由于各分段曲线受曲线弧长、Jmax、Amax等约束后，S曲线5段规划后的速度和多项式5段规划后的速度都所降低，S曲线5段插补整段曲线平均速度为615.88mm/s，多项式5段插补整段曲线平均速度为535.84mm/s。但多项式加减速规划后的速度更平滑过渡，在最大速度附近的速度变化更柔和。

如图6所示为S曲线5段与多项式5段控制方法的加速度曲线，S曲线5段控制方法的加速度控制在±8000mm/s2之内，而多项式5段规划后的加减速控制在±5400mm/s2，上述两种方法都满足了机床加速度的要求。但S曲线5段加减速规划后的加速度变化比较尖锐，多项式5段加减速规划后的加速度较为平缓。

图5 S曲线5段与多项式5段规划后的速度曲线

图6 S曲线5段与多项式5段规划后的加速度曲线

如图7所示为S曲线5段与多项式5段规划后的加加速度曲线，所得到加加速度都限制在Jmax内。S曲线5段规划后的加加速度曲线存在多次跳跃式的变化，引起机床的震颤；而多项式5段规划后的加速度和加加速度为连续变化，速度和加速度曲线更为平缓柔和，使机床有更好的柔性。表2所示为两种加减速方法的结果比较。

图7 S曲线5段与多项式5段规划后的加加速度曲线

方法插补时间(s)最大加速度(mm/s2)最大加加速度(mm/s3)柔性S曲线5段加减速算法2.010800080000一般多项式5段加减速算法2.321540080000好

表2从以下几个方面进行了对比：插补时间、所达到的最大加速度、最大加加速度、系统柔性等。可以看出S曲线运行时间短，柔性一般；而多项式5段运行时间长，但具有良好的柔性。不难发现系统柔性提高则运行时间增加，图1所示的NURBS曲线长度为1267.8616mm，但多项式5段的加工时间只比S-5段多花0.311s。在高速高精度加工中，要求数控机床冲击振动小、柔性好。结果表明，多项式5段加减速控制方法优于S曲线5段控制方法，前者更满足于复杂高精度的NURBS曲线加工要求。

5 结束语

提出基于多项式5段加减速的NURBS插补控制方法，首先根据自适应速度控制方法对曲线进行分段，并对分段后NURBS曲线弧长、初始(终点)速度要求来进行分析确定加减速类型，从而对NURBS曲线全程进行规划。在设定的各种约束前提下，保证了加速度、加加速度连续变化，速度平滑性好。与S曲线5段加减速的NURBS插补控制方法相比，提高了机床系统柔性降低了加减速过程中的冲击，仿真验证所提方法的有效性。

[参考文献]

[1] Qiang L, Liu H, Yuan S. High Accurate Interpolation of NURBS Tool Path for CNC Machine Tools[J]. Chinese Journal of Mechanical Engineering, 2016, 29(5):911-920.

[2] Piegl L, Tiller W. The NURBS book[M]. 2nd . New York:Springer-Verlag Inc.,1997.

[3] 赵玉刚,李伟,郭峰,等. 基于Cox-de Boor递推的任意次NURBS曲线插补算法的研究与仿真[J]. 组合机床与自动化加工技术,2012(6):45-48.

[4] 梁宏斌, 王永章, 李霞. 自动调节进给速度的NURBS插补算法的研究与实现[J]. 计算机集成制造系统, 2006, 12(3):428-433.

[5] 潘海鸿, 杨微, 陈琳,等. 全程S曲线加减速控制的自适应分段NURBS曲线插补算法[J]. 中国机械工程, 2010,21(2):190-195.

[6] 周胜德, 梁宏斌, 乔宇. 基于NURBS曲线插补的五段S曲线加减速控制方法研究[J]. 组合机床与自动化加工技术, 2011(4):37-41.

[7] 岳磊, 赵国勇, 刘晨希,等. 基于S曲线加减速的NURBS插补控制方法研究[J]. 组合机床与自动化加工技术, 2015(5):43-46.

[8] 于金刚, 林浒, 张晓辉,等. 一种新型的Jerk连续加减速控制方法研究[J]. 组合机床与自动化加工技术, 2009(8):61-64.

[9] 徐川, 王永章, 刘源. 多项式加减速控制方法研究[J]. 组合机床与自动化加工技术, 2009(9):42-44.

[10] 张振华. 数控系统加减速算法及定位技术研究[D]. 大连:大连理工大学, 2007.

[11] 颜庆津. 数值分析[M]. 4版. 北京:北京航空航天大学出版社, 2012.