非自治广义Birkhoff系统的半负定矩阵梯度系统表示*

王嘉航，张毅

（1.苏州科技大学土木工程学院，江苏苏州215011；2.河海大学土木与交通学院，江苏南京210098）

梯度系统是一个数学系统，梯度系统是微分方程和动力系统研究中的重要问题[1-3]。如果一个力学系统能够化成为梯度系统，就可利用梯度系统的特性来研究力学系统的性质，特别是解的积分和系统的稳定性[4]。梅凤翔等[5-11]研究了 Lagrange系统、Hamilton系统和Birkhoff系统的梯度系统方法和斜梯度系统方法，陈向炜等[12]用具有负定非对称矩阵的梯度系统构造稳定的广义Birkhoff系统，曹秋鹏等[13-14]利用梯度系统方法研究了一类非自治广义Birkhoff系统的稳定性和分岔和约束自治广义Birkhoff系统平衡稳定性，李彦敏等[15]研究了非自治Birkhoff系统的广义斜梯度表示，陈向炜等[16]研究了广义Birkhoff系统稳定性对双参数的依赖关系，张毅等[17-20]研究了一类非自治Birkhoff系统的梯度表示。本文进一步研究非自治广义Birkhoff系统成为具有半负定矩阵梯度系统的条件，并利用半负定矩阵梯度系统的性质来研究非自治广义Birkhoff系统的稳定性。

1 半负定矩阵的梯度系统

半负定矩阵梯度系统的微分方程表示为[2]

其中aij（X）为半负定矩阵，V称为能量函数。考虑半负定矩阵aij（X）的性质，可得

如果函数V为Lyapunov函数，则可以利用Lyapunov定理判断解的稳定性。因此，如果函数V在解的领域附近是正定的，根据Lyapunov定理，可知解是稳定的。如果函数V不能成为Lyapunov函数，在一定条件下，有可能利用Rumyantsev关于部分变量稳定性定理来研究梯度系统的部分变量稳定性。

2 非自治广义Birkhoff系统的梯度表示

广义Birkhoff系统的运动微分方程为

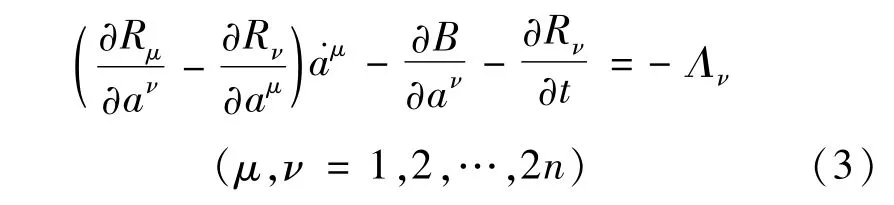
其中B＝B（t，a）为Birkhoff函数，Rμ＝Rμ（t，a）为Birkhoff函数组，Λν＝Λν（t，a）为附加项。如果Birkhoff函数B和Birkhoff函数组Rμ都显含时间t，则称系统为非自治的。

假设系统非奇异，则方程（3）可表示为

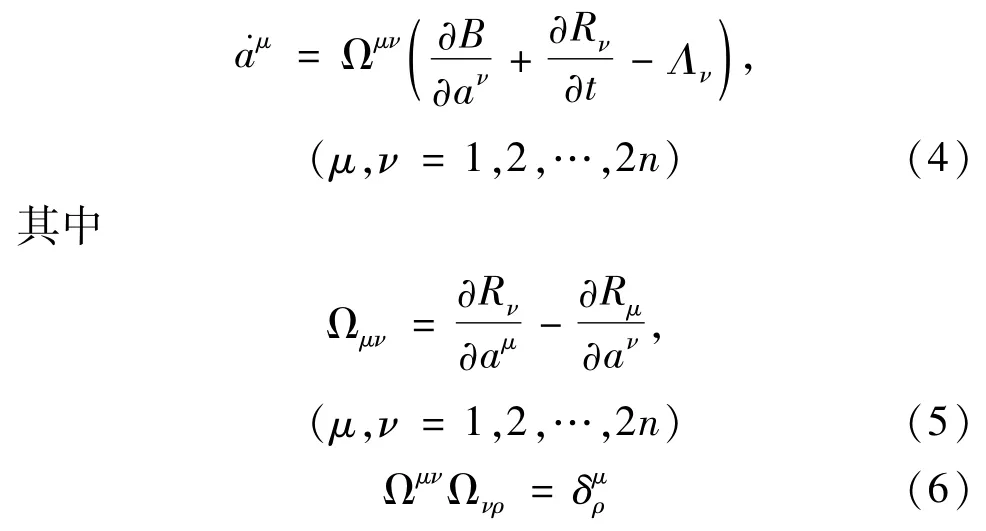
一般而言，非自治广义Birkhoff系统不是一个梯度系统。如果能量函数V满足条件

显然这是一个半负定矩阵的梯度系统。因此在满足条件（7）时，非自治广义Birkhoff系统为半负定矩阵的梯度系统。

3 举 例

例1 二阶非自治广义Birkhoff系统的Birkhoff函数Birkhoff函数组为

附加项为Λ1＝2a1et-a2et，Λ2＝0，试将其化为半负定矩阵梯度系统，并讨论零解的稳定性。

解：由式（5）-（6）计算得

于是广义Birkhoff方程为

可写成如下形式

其中矩阵是半负定的，则能量函数V为

V在a1＝a2＝0的邻域内正定的，因此零解a1＝a2＝0是稳定的。

例2二阶非自治广义Birkhoff系统的Birkhoff函数组为

附加项为

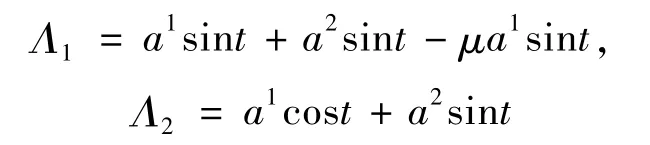
其中μ是参数，试将其化为半负定矩阵梯度系统，并讨论零解的稳定性。

解：广义Birkhoff方程为

也可写成如下形式

其中矩阵是半负定的，则能量函数V为

当-1＜μ＜1时，V在a1＝a2＝0的邻域内是正定的，因此零解a1＝a2＝0是稳定的。

4 结 语

在力学系统的稳定性研究中，构造Lyapunov函数有时很困难的，而运用梯度系统的性质研究稳定性不需要构造Lyapunov函数。本文利用半负定矩阵梯度系统的性质来研究非自治广义Birkhoff系统的稳定性问题，将非自治广义Birkhoff系统在一定条件化为具有半负定矩阵梯度系统，算例表明了结果的有效性。

[1]HIRCH M W，SMALE S.Differential equations，dynamical systems and linear algebra[M].New York：Academic Press，1974.

[2]MC LACHLAN R I，QUISPEL G R W，ROBIDOUX N.Geometric integration using discrete gradients[J].Phil Tran R Soc Lond A，1999，357：1021-1045.

[3]HIRSCH M W，SMALE S，DEVANEY R L.Differential equations，dynamical systems，and introduction to chaos[M].Singapore：Elsevier，2008.

[4]梅凤翔，吴惠彬.约束力学系统的梯度表示[M].北京：科学出版社，2016.

[5]梅凤翔.关于梯度系统[J].力学与实践，2012，34（1）：89-90.MEI FX.About gradient system[J].Mechanics in Engineering，2012，34（1）：89-90.

[6]梅凤翔，吴惠彬.广义Birkhoff系统的梯度表示[J].动力学与控制学报，2012，10（4）：289-292.MEI F X，WU H B.A gradient representation for generalized Birkhoff system[J].Journal of Dynamics and Control，2012，10（4）：289-292.

[7]梅凤翔，吴惠彬.Birkhoff系统的广义斜梯度表示[J].动力学与控制学报，2015，13（5）：329-331.MEI F X，WU H B.Generalized skew-gradient representation for Birkhoff system[J].Journal of Dynamics and Control，2015，13（5）：329-331.

[8]梅凤翔，吴惠彬.广义Birkhoff系统与一类组合斜梯度[J].物理学报，2015，64（18）：366-370.MEI F X，WU H B.Generalized Birkhoff system and a kind of combined gradient system[J].Acta Phys Sin，2015，64（18）：366-370.

[9]MEI F X，WU H B.Bifurcation for the generalized Birkhoffian system[J].Chin Phys B，2015，24（5）：054501.

[10]MEI F X，WU H B.Skew-gradient representation of generalized Birkhoffian system[J].Chin Phys B，2015，24（10）：104502.

[11]MEI F X，CUIJC.Skew-gradient representation of constrained mechanical system[J].Applied Mathematics and Mechanics，2015，36（7）：873-882.

[12]陈向炜，张晔，梅凤翔.用具有负定非对称矩阵的梯度系统构造稳定的广义 Birkhoff系统[J].力学学报，2017，49（1）：149-153.CHEN X W，ZHANG Y，MEI F X.Stable generalized Birkhoff systems constructed by using a gradient system with non-symmetrical negative-definite matrix[J].Chinese Journal of Theoretical and Applied Mechanics，2017，49（1）：149-153.

[13]曹秋鹏，陈向炜.一类非自治广义Birkhoff系统的稳定性和分岔[J].北京大学学报，2016，52（4）：653-657.CAO Q P，CHEN X W.Stability and bifurcation for a type of non-autonomous generalized Birkhoffian system[J].Acta Scientiarum Naturalium Universitatis Pekinensis，2016，52（4）：653-657.

[14]曹秋鹏，张毅，陈向炜.约束自治广义Birkhoff系统平衡稳定性的梯度系统方法[J].云南大学学报，2015，37（2）：228-232.CAO QP，ZHANGY，CHENX W.Stability of equilibrium for autonomous generalized Birkhoffian system with constraints by gradient system[J].Journal of Yunnan University，2015，37（2）：228-232.

[15]李彦敏，梅凤翔.非自治Birkhoff系统的广义斜梯度表示[J].云南大学学报，2015，37（6）：832-836.LI Y M，MEI F X.A generalized skew-gradient representation for non autonomous Birkhoffian system[J].Journal of Yunnan University，2015，37（6）：832-836.

[16]陈向炜，曹秋鹏，梅凤翔.广义Birkhoff系统稳定性对双参数的依赖关系[J].力学季刊，2017，38（1）：108-112.CHEN X W，CAO Q P，MEI F X.Ascendance of stability of generalized Birkhoff system on two parameters[J].Chinese Quarterly of Mechanics，2017，38（1）：108-112.

[17]张毅.一类非自治Birkhoff系统的梯度表示[J].苏州科技学院学报，2015，32（4）：1-3.ZHANG Y.A gradient representation for a type of nonautonomous Birkhoffian system[J].Journal of Suzhou University of Science and Technology，2015，32（4）：1-3.

[18]王雪萍，张毅.Birkhoff系统的Noether-Mei对称性与守恒量[J].中山大学学报（自然科学版），2016，55（4）：53-55.WANG X P，ZHANG Y.Noether-Mei symmetry and conserved quantity of Birkhoffian system[J].Acta Scientiarum Naturalium Universitatis Sunyatseni，2016，55（4）：53-55.

[19]LIU C，LIU SX，MEI F X.Stability analysis of a simple rheonomic nonholonomic constrained system[J].Chin Phys B，2016，25（12）：124501.

[20]张毅.相空间中类分数阶变分问题的Noether对称性与守恒量[J].中山大学学报（自然科学版），2013，52（4）：45-50.ZHANG Y.Noether symmetry and conserved quantity for a fractional action-like variational problem in phase space[J].Acta Scientiarum Naturalium Universitatis Sunyatseni，2013，52（4）：45-50.

[21]梅凤翔.分析力学[M].北京：北京理工大学出版社，2013.

[22]梅凤翔.广义Birkhoff系统动力学[M].北京：北京理工大学出版社，2013.