一种BDS单历元整周模糊度固定的解算方法

李 博，徐爱功，祝会忠，高 猛，龚宵雪

(辽宁工程技术大学 测绘与地理科学学院，辽宁 阜新 123000)

0 引言

北斗卫星导航系统(BeiDou navigation satellite system，BDS)是全球四大卫星导航系统之一；随着BDS的建设和不断完善，BDS在高精度定位中扮演着重要的角色。载波相位整周模糊度准确固定是高精度BDS动态定位的核心问题[1-2]，而准确固定整周模糊度一般需要多个历元的观测数据，并且需要对载波相位观测数据进行周跳探测，当卫星信号失锁时重新求解整周模糊度会使数据处理过程变得十分复杂[3-4]。采用单历元观测数据确定整周模糊度则不需要考虑周跳问题，也不用担心卫星信号失锁时重新求解整周模糊度的问题，可以缩短确定模糊度的时间、提高解算效率。对于单历元整周模糊度的解算方法，已有许多学者进行了研究：文献[5]提出附有基线约束的LAMBDA方法，对LAMBDA算法用2步搜索方法进行优化，使得固定单频单历元的整周模糊度成功率较高；文献[6]提出一种组合的模糊度搜索方法，运用到有LAMBDA算法辅助的基线上，确保单历元算法的精度和成功率，并指出准确的先验约束信息是上述单历元模糊度解算的关键因素，而常规的基线解算过程通常是无法获取或不存在这些先验信息的；文献[4]采用2种不同线性组合的扩波方法来缩小模糊度的搜索空间，并对其进行逆变换，进而用模糊度函数法来搜索真值，获得了较好的结果；文献[7]提出一种利用多频观测值、基于有几何模型的逐级模糊度固定方法，通过依次固定超宽巷、宽巷、窄巷模糊度来实现模糊度的快速固定；文献[3]对宽巷模糊度进行主、从模糊度的区别来解算单历元模糊度；文献[8]提出对单频单历元模糊度求解时进行随机模型精化，并得到有益结论。利用载波相位观测值进行BDS短基线单历元最小二乘解算时，法方程是秩亏的，而利用测码伪距观测值和双频载波相位观测值组成双差观测方程时，伪距观测值的低精度使得模糊度浮点解精度不高，造成模糊度组合有过大的搜索空间，从而不能得到准确的整周模糊度。

本文利用正则化方法消除法方程的秩亏问题，以获得较高精度的宽巷浮点模糊度；同时应用均方误差矩阵代替协方差阵确定模糊度的搜索范围，以提高搜索效率；并将确定后的宽巷整周模糊度代入由宽巷和载波相位双差观测值组成的联合观测方程中，改进所有参数，然后采用LAMBDA算法便可直接固定B1/B2整周模糊度。

1 BDS单历元整周模糊度解算的基本原理

1.1 BDS单历元整周模糊度解算的数学模型

在短基线数据处理时，双差可以消除卫星钟差、接收机钟差，并削弱卫星轨道误差、电离层延迟和对流层延迟等误差[9]；因此本文对BDS单历元整周模糊度解算过程进行双差处理。

设2台接收机在某历元可同步观测k+1颗卫星，组成k个相位双差观测方程，其线性化后[10]为

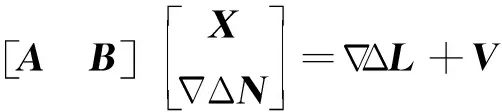
(1)

式(1)可简写成

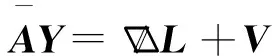
(2)

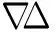
根据最小二乘原则，由式(2)组成法方程，得到最小二乘法(least square method，LS)解

(3)

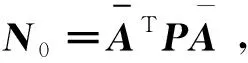
(4)

1.2 双差整周模糊度单历元解算

由于B1、B2载波相位宽巷观测值的波长达84.7 cm，因而很容易固定其整周模糊度[11]；所以在基线解算时，先固定宽巷的整周模糊度，其线性化后的宽巷双差观测方程简写为

(5)

式中：Aw为宽巷的系数矩阵；Bw为宽巷的模糊度系数矩阵；Nw为k个宽巷的双差整周模糊度；Lw为宽巷的双差观测值与计算值之差；Vw为宽巷观测值的真误差。

宽巷模糊度准确固定之后，将宽巷双差观测值和载波相位双差观测值组成新的联合观测方程为

(6)

式中：A1为B1载波的系数矩阵；Β1为B1载波的模糊度系数矩阵；N1为k个B1载波的双差整周模糊度；L1为B1载波的双差观测值与计算值之差；λw为宽巷的波长；V1为B1载波的观测值真误差。新的联合观测方程由于确定的宽巷模糊度转化成了精度较高的距离值[12]，得到了精度较高的浮点解和状态明显改善的协方差矩阵，从而采用LAMBDA算法可直接固定B1载波的整周模糊度。B2载波的双差整周模糊度N2与N1、Nw有如下的线性关系：N2=N1-Nw，即B1载波的整周模糊度固定之后，B2载波的整周模糊度也随即固定。本文只求解B1载波的整周模糊度。

所以在基线解算时，准确固定宽巷的模糊度非常重要。由于式(5)的未知数个数大于观测方程个数，因此该方程为秩亏方程，且秩亏数为3。法矩阵的非满秩将导致最小二乘解不唯一；要想得到唯一解，须附加约束条件。

2 基于正则化的载波相位解算模型

本文运用正则化解决法方程秩亏问题。根据Tikhonov正则化原理，求解式(2)采用的估计准则[10]为

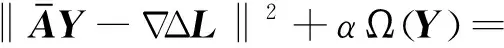
(7)

式中：α为平滑因子或正则化参数；R为正则化矩阵；Ω(Y)为稳定泛函；‖•‖表示欧氏2-范数。正则化准则对稳定泛函Ω(Y)极小作了约束，因此有利于解算法矩阵的秩亏问题。

2.1 构造正则化矩阵R

将式(2)中的观测值L的权矩阵P单位化，得到

(8)

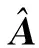
(9)

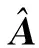
将Q、D矩阵进行分块法处理，得

(10)

(11)

式中：Q11、Q12、Q21、Q22为矩阵Q的子块；D1、D2为奇异值矩阵D的子块。

令

(12)

构造正则化矩阵

(13)

2.2 确定正则化参数α

构造矩阵R后，运用L曲线法进行大量的计算，结果表明当参数α=1时效果最好[10]。则式(7)变为

(14)

结合式(2)由估计准则式(14)求导组成的法方程为

(15)

解算该法方程，得

(16)

式中R为k×k阶奇异矩阵，其左上角3×3子矩阵为满秩矩阵，其余元素为0。与式(3)中的法方程系数阵N0相比，式(15)系数阵中增加了正则化矩阵R，就相当于增加了3个约束条件，使得法矩阵为满秩矩阵，采用最小二乘法得到唯一解。

相应的均方误差矩阵RMSEM近似取为

(17)

3 实验及结果分析

为了验证该方法，对BDS双频接收机采集的长度为5.8 km的基线进行静态单历元基线解算。选取28 min的观测数据，采样间隔为1 s，卫星截止高度角设为15o。本文所涉及的模糊度固定值以多历元基线解算求得的模糊度固定值为真实值。

Ratio值可作为模糊度得到固定解的置信度指标，Ratio值定义为次最小单位权方差与最小单位权方差之比[9]。本文取Ratio值的阈值为3，当Ratio值大于阈值时，认为模糊度固定正确。以下给出了固定宽巷整周模糊度的Ratio值，如图1所示。

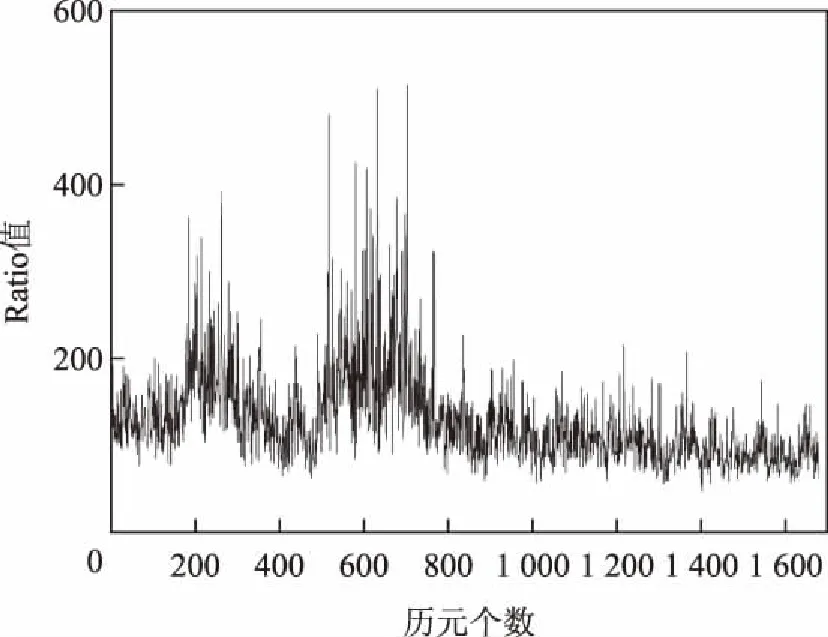
图1 宽巷整周模糊度的Ratio值

由图中可知，宽巷整周模糊度的Ratio值大部分稳定在100左右，少部分主要可能受对流层湿延迟的残余误差影响较小而达到300至500，其最小值为47，远大于阈值3；所以本文提出的方法所固定的宽巷整周模糊度是可靠的。

为了更明显地显示正则化后固定宽巷整周模糊度的效果，以第1个历元为例，将正则化前后2种方案求得的宽巷模糊度浮点解和固定解进行比较，如表1所示。

表1 2种方案下的宽巷模糊度浮点解和固定解

从表中可以看出：由于正则化前法方程的病态，最小二乘的浮点解严重偏离真值，无法搜索出整周模糊度；而正则化后宽巷模糊度的浮点解与真实值的偏差在0.5个周期左右，可快速且容易固定其整周模糊度，成功率达到100 %。

将固定后宽巷整周模糊度代入式(6)，其已转化成精度较高的距离值，使新的联合观测方程得到精度较高的浮点解和状态明显改善的协方差矩阵，采用LAMBDA算法可直接固定B1载波的整周模糊度。仍以第1个历元为例，B1频率模糊度的浮点解和固定解如表2所示。

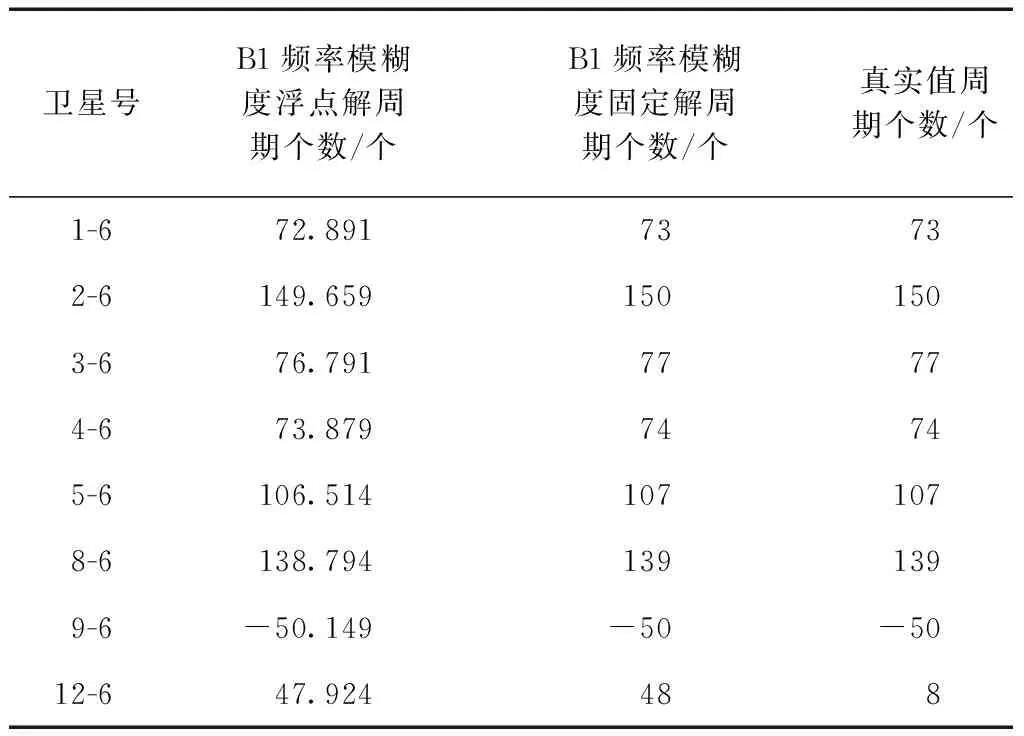
表2 B1频率模糊度的浮点解和固定解

由表可知，当宽巷模糊度正确固定之后，B1频率的模糊度就可快速准确地固定，成功率达到100 %。如图2所示，可得B1频率模糊度在东(E)、北(N)、天顶(U)3个方向上解算的坐标精度。

由图中可知，E方向和N方向的坐标偏差值变化范围在1.5 cm之内，U方向的坐标偏差值在5.5 cm以内；再次证明了本文算法固定模糊度的准确性。

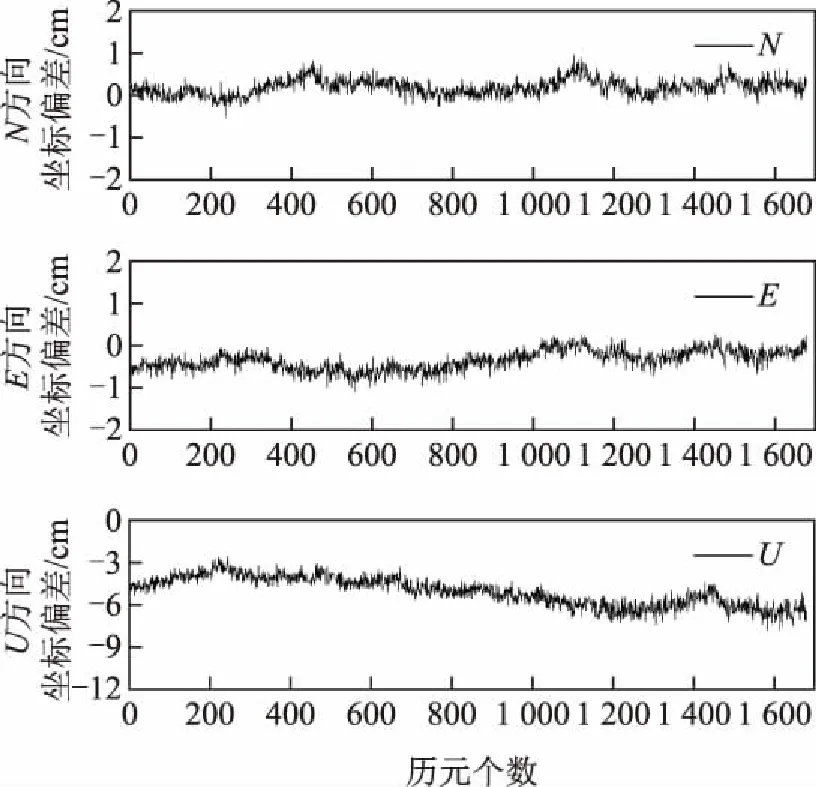
图2 L1频率模糊度解算的坐标偏差

均方根误差(root mean square error,RMSE)是外部符合精度的指标，主要反映了观测值与参考值的偏差程度[13]；所以为了便于定量分析，对正则化方法在E、N、U方向上得到的偏差进行概率统计，求出其RMS值，如表3所示。

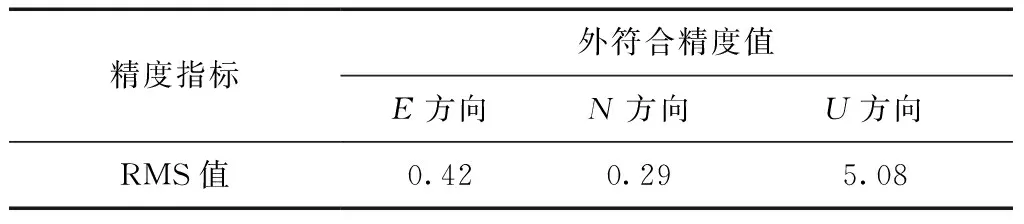
表3 基线解算在E、N、U方向上的RMS值 cm

由表中可以看出：E、N方向的RMSE值分别为4.2和2.9 mm；U方向较E、N方向的精度相对较差，但其精度也在厘米级范围内，为5.08 cm。

4 结束语

本文针对BDS短基线单历元解算过程中法方程严重病态的问题，利用正则化方法对法方程进行改进，获得了较高精度的宽巷浮点模糊度；宽巷整周模糊度确定之后，利用宽巷双差观测值和载波相位双差观测值组成新的联合观测方程；而由于宽巷整周模糊度转化成了精度较高的距离值，使新的联合观测方程得到了精度较高的浮点解和状态明显改善的协方差矩阵；再采用LAMBDA算法可直接固定B1载波的整周模糊度。本文提出的方法解决了解算短基线单历元时法方程的严重病态问题，在得到了较准确的模糊度浮点解的同时，应用均方误差矩阵代替协方差阵确定模糊度的搜索范围，提高了搜索效率，使单历元模糊度固定成功率可以达到100 %。

[1] 卢立果，刘万科，李江卫.降相关对模糊度解算中搜索效率的影响分析[J].测绘学报，2015，44(5)：481-487.

[2] 李豹，许江宁，曹可劲，等.改进LAMBDA算法实现单频GPS整周模糊度快速解算[J].中国惯性技术学报，2013，21(3)：365-368.

[3] 祝会忠，高星伟，秘金钟，等.一种GPS整周模糊度单历元解算方法[J].测绘科学，2011，36(4)：9-11.

[4] 刘宁，熊永良，王德军，等.一种新的GPS整周模糊度单历元求解算法[J].武汉大学学报(信息科学版)，2013，38(3)：291-294.

[5] 唐卫明，孙红星，刘经南.附有基线长度约束的单频数据单历元LAMBDA方法整周模糊度确定[J].武汉大学学报(信息科学版)，2005，30(5)：444-446.

[6] 李征航，刘万科，楼益栋，等.基于双频GPS数据的单历元定向算法研究[J].武汉大学学报(信息科学版)，2007，32(9)：753-756.

[7] 刘炎炎，叶世榕，江鹏，等.基于北斗三频的短基线单历元模糊度固定[J].武汉大学学报(信息科学版)，2015，40(2)：209-213.

[8] 王振杰，王心众，范士杰，等.一种考虑随机模型精化的单频单历元算法[J].全球定位系统，2011，36(5)：1-5.

[9] 李征航，黄劲松.GPS测量与数据处理[M].武汉：武汉大学出版社，2012：155-158.

[10] 卢秀山，王振杰，欧吉坤，等.单频GPS短基线快速定位中的少数历元算法[J].武汉大学学报(信息科学版)，2007，32(12)：1147-1151.

[11] 祝会忠，徐爱功，高猛.北斗系统载波相位动态差分定位方法[J].测绘科学，2015，40(9)：9-13.

[12] 高猛，徐爱功，祝会忠，等.北斗系统短基线解算数据处理方法[J].测绘科学，2015，40(4)：28-33.

[13] 杨元喜.卫星导航的不确定性、不确定度与精度若干注记[J].测绘学报，2012，41(5)：646-650.