GPS/BDS/Galileo相位平滑伪距单点定位性能分析

邝英才，吕志平，李林阳，黄 娴

(1.信息工程大学 地理空间信息学院，郑州 450001；2.河南工业大学，郑州 450001)

0 引言

全球导航卫星系统(global navigation satellite system，GNSS)测码伪距观测值不存在整周模糊度的求解问题，但其精度远低于载波相位观测值。为了减小伪距观测值误差的影响，提高其精度，文献[1]最早提出可以利用载波相位的变化来平滑伪距。文献[2]指出传统载波相位平滑伪距公式没有考虑平滑历元次数增多的相位观测误差对定位精度不可忽略的影响，并论证了双频载波相位平滑伪距算法；文献[3-4]比较了载波相位平滑伪距和卡尔曼滤波，提出结合二者能有效提高定位精度及稳定度。由于载波相位平滑伪距技术具有良好的抗差性、实时性、易实现性，目前其在基线解算、GNSS地基增强系统、实时动态导航定位等方面已得到了较为广泛的应用[5-7]。

近些年，对于载波相位平滑伪距对精度影响的研究已经有了一定进展。文献[8-10]研究了全球定位系统(global positioning system，GPS)、北斗卫星导航系统(BeiDou navigation satellite system，BDS)单频相位平滑伪距，但没有涉及双频载波相位平滑伪距；文献[11-12]对比分析了GPS及GPS/BDS组合系统双频相位平滑伪距与伪距单点定位结果，但并未涉及对伽利略卫星导航系统(Galileo satellite navigation system，Galileo)平滑效果的分析。

本文利用多模GNSS实验跟踪网(multi-GNSS experiment，MGEX)多站多天的实测数据，从收敛速度、定位精度、定位结果标准偏差、多天平滑效果稳定性几个方面对GPS、BDS、Galileo系统双频载波相位平滑伪距前后的定位结果进行了对比分析。

1 双频载波相位平滑伪距

GNSS解调导航信号后得到测码伪距和载波相位观测值，其非差观测方程为

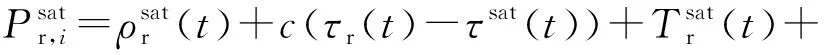
(1)

(2)

利用非差无几何组合观测值可推导双频载波相位平滑伪距的递推公式。文献[13]从无偏性角度推导了双频载波相位平滑伪距的表达式，以P1码为例，在任一历元s内可得

(3)

(4)

由式(3)和式(4)可以得到易于编程实现的双频载波相位平滑伪距递推公式为

(5)

本文选择双频平滑改正模型处理电离层延迟。对比缺少实际观测量的电离层延迟经验改正模型，双频GNSS接收机可利用伪距观测值和载波相位观测值中的电离层信息计算得到更精确的延迟改正量；在最坏情况下，误差一般也只为数毫米[14]。同时考虑到伪距观测值计算的电离层延迟量噪声大、精度较差，载波相位观测值受整周模糊度参数限制只能得到相对改正量[15]，建立该模型常用到的观测值为经载波相位平滑处理后的伪距观测值。以P1码为例，类似式(5)可得到历元s时刻的电离层延迟改正量为

(6)

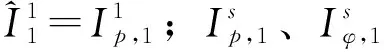
在讨论一系列数据分布的离散程度时，常用到的评估指标是标准差(standard deviation，Std)，其计算公式为

(7)

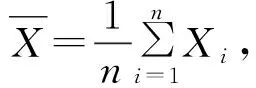
2 实验与结果分析

2.1 实验模型及参数估计方法

实验采用MGEX 6个站多天的数据，每天共2 853个连续历元的GPS、BDS和Galileo观测量，采样间隔为30 s。

表1 观测模型及参数估计设置

2.2 可见卫星数量分析

以CUT0站和KIRU站为例，设置年积日(day of year，DOY)，取DOY为第327天，分别计算3个系统下当天任意时刻的可见卫星数，如图1所示。

从图中可以看出：GPS系统可见卫星数量是3个系统中最多的，卫星数最少的时候也有7颗，比大部分时候另外2个系统的可见卫星数均要多；而BDS系统和Galileo系统在某些时刻会出现可见卫星数极少的情况，甚至只有1颗，很难保证其定位精度，这也是目前BDS系统和Galileo系统定位精度提升受限的一个重要原因。

为更直观地比较3个系统可见卫星数差异，分别统计了第327天、第328天、第329天不同系统不同地区测站的平均可见卫星数量，如表2所示。

图1 CUT0和KIRU站GPS、BDS、Galileo可见卫星数量

表2 不同系统平均可见卫星数对比 颗

从表2中可以看出：不同地区的GPS系统卫星可见数量均远远超过另外2个系统，平均可见卫星在9颗以上；Galileo系统在初始服务逐渐启动后，发射了新的卫星[16]，其可见卫星数量目前稳定在3颗以上；除去我国的JFNG站和澳大利亚的CUT0站，Galileo系统各天的可见卫星数量均多于BDS系统，尤其是在BDS卫星可见数量较少的欧洲测站观测范围内。对比另外2个系统，BDS系统卫星目前在欧洲地区可见数量较少；相信在BDS系统进一步全球化之后，系统在全球范围内的可见卫星数量将会得到一定提升。

2.3 平滑前后收敛速度分析

以METG站为例分析平滑前后滤波定位结果的收敛速度。连续3 d的定位解算中，本文在同一系统同一方向上选择同一收敛条件，即从某一历元开始至结束历元的任意时刻中，坐标偏差绝对值均小于所给阈值，则此历元视为收敛历元，此时滤波视为收敛。

GPS系统的收敛情况如图2所示。GPS系统在N、E、U方向上设定的收敛阈值分别为3、1、3 m。

从图中可以看出，连续3 d的时间里：N方向上滤波平滑前至少需要9.7 h才能达到收敛条件；U方向上3 d平滑前的定位滤波均未达到收敛条件，平滑后所有历元坐标偏差绝对值均小于阈值；E方向上平滑前至少需要9.4 h滤波才能达到收敛条件，平滑后最多只需要8.4 h。3个方向上平滑后收敛速度均有明显提升。

BDS系统的收敛情况如图3所示。BDS系统在N、E、U方向上设定的收敛阈值分别为10、3、5 m。

从图中可以看出，连续3 d的时间里：N方向上平滑前至少需要8.3 h滤波才能达到收敛条件，平滑后最多只需要4 h；E方向上平滑后至多能将收敛时间减少8.2 h；U方向上定位滤波在平滑后至多提前了4.6 h达到收敛条件。对比GPS系统，平滑对收敛速度的影响稍小。

Galileo系统的收敛情况如图4所示。Galileo系统在N、E、U方向上设定的收敛阈值分别为5、2、5 m。

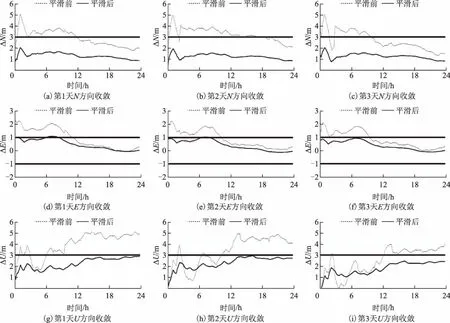
图2 GPS系统连续3 d METG站平滑前后收敛速度对比

图3 BDS系统连续3 d METG站平滑前后收敛速度对比

图4 Galileo系统连续3 dMETG站平滑前后收敛速度对比

从图4中可以看出，连续3 d的时间里：N方向和E方向上滤波平滑后分别至少提前了3.5、1.9 h达到收敛条件，平滑后E方向上滤波收敛至多能提前13.9 h；U方向上平滑前有2 d的定位滤波未达到收敛条件，平滑后定位滤波均能收敛，而平滑前能收敛的定位滤波平滑后提前了1.1 h收敛。Galileo系统平滑前后收敛速度的提升效果好于BDS系统，但仍然差于GPS系统。

计算各站平滑前后收敛速度的加速比如表3所示。对于部分测站在某些方向上平滑前未收敛到阈值或者平滑后所有历元坐标偏差绝对值均小于阈值的情况，其加速比用横线表示。

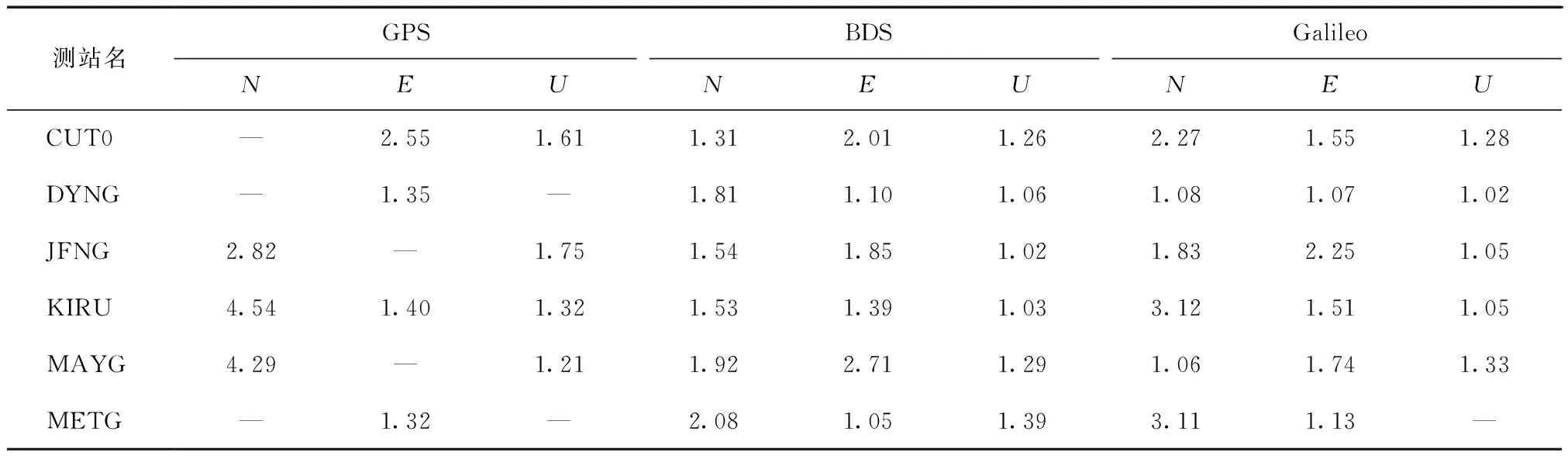
表3 3个系统各站平滑前后收敛加速比

由表3中数据可知：3个系统平滑后滤波收敛速度均有所提升；其中，较之另外2个系统，GPS系统收敛速度在平滑前后提升最明显；对比3个方向，N方向较之E、U方向，平滑前后收敛速度提升效果较明显；平滑前定位滤波不能收敛的情形在平滑后均得到很好的改善，当天能够收敛。

2.4 平滑前后定位精度分析

以MAYG站为例，分别计算3个系统下该站在年积日第327天全天任意历元N、E、U方向上的定位偏差，如图5所示。

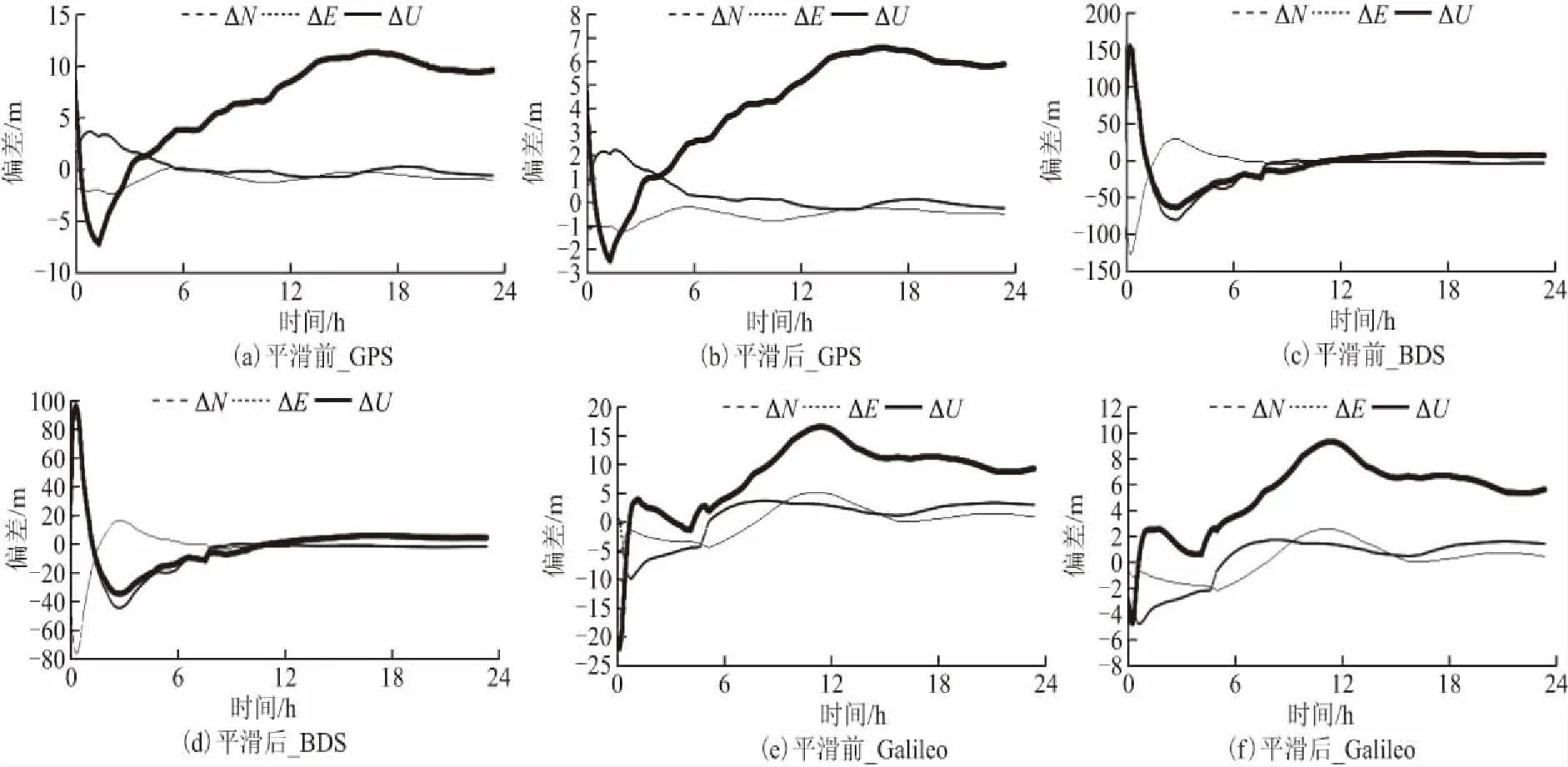
图5 3个系统MAYG站平滑前后定位结果对比

从图5中可以看出，平滑前后：GPS系统3个方向上的定位结果区间从[-10，15]缩小到[-3，8]；BDS系统3个方向上的定位结果区间从[-150，200]缩小到[-80，100]；Galileo系统3个方向上的定位结果区间从[-25，20]缩小到[-8，12]，3个系统平滑后全天的定位结果坐标偏差波动区间均缩小了接近50 %。

为更直观地对比平滑前后定位结果，本文将定位时段最后一个历元的坐标偏差绝对值视为整个时段的整体定位精度指标。图6为3个系统下DYNG站在年积日第327天N、E、U3个方向上的定位结果精度对比。

由图可知，平滑后3个系统下该站在任一方向上的定位精度均有提高；其中所有系统的U方向平滑后精度均明显提高；GPS系统下该站在U方向上平滑后精度改善最明显。

统计3个系统各站第327天平滑前后的定位精度变化并加入标准差的对比，可得如表4、表5、表6所示的结果。

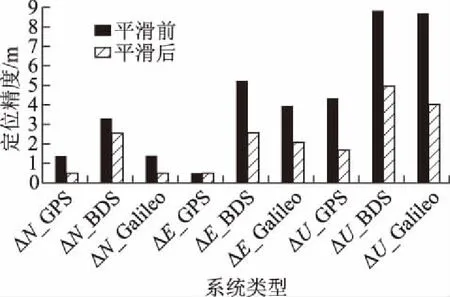
图6 3个系统DYNG站平滑前后定位结果精度对比

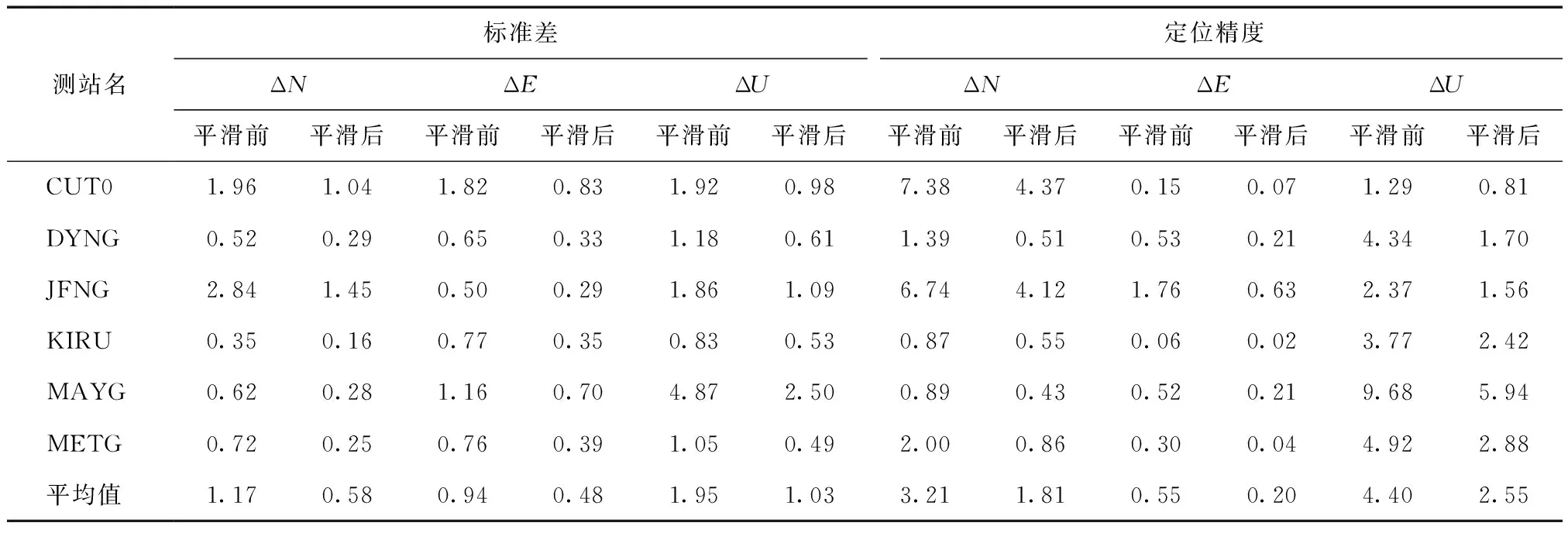
表4 GPS系统各站平滑前后标准差及定位精度对比 m

由表中数据可知，所有测站的定位结果在平滑后精度均有所提高，标准差均减小。3个系统的三维定位结果精度从5.47、10.14、6.69 m提升到3.13、5.66、3.63 m，分别提高了1.75、1.79、1.84倍。其中，BDS系统平滑前定位结果精度较差，平滑后得到很好的改善。平滑前，GPS系统整体定位结果标准差最小，BDS系统整体定位结果标准差最大，造成这一现象的原因可能是BDS观测噪声偏大。平滑后，3个系统各方向的测站标准差平均值均减小了45 %以上，说明经平滑处理后，24 h内滤波定位分布的波动减小，明显的跳跃减少，结果更加稳定。其中，Galileo系统各方向的标准差减小率均达到50 %，平滑对滤波定位结果稳定性的提高最明显。

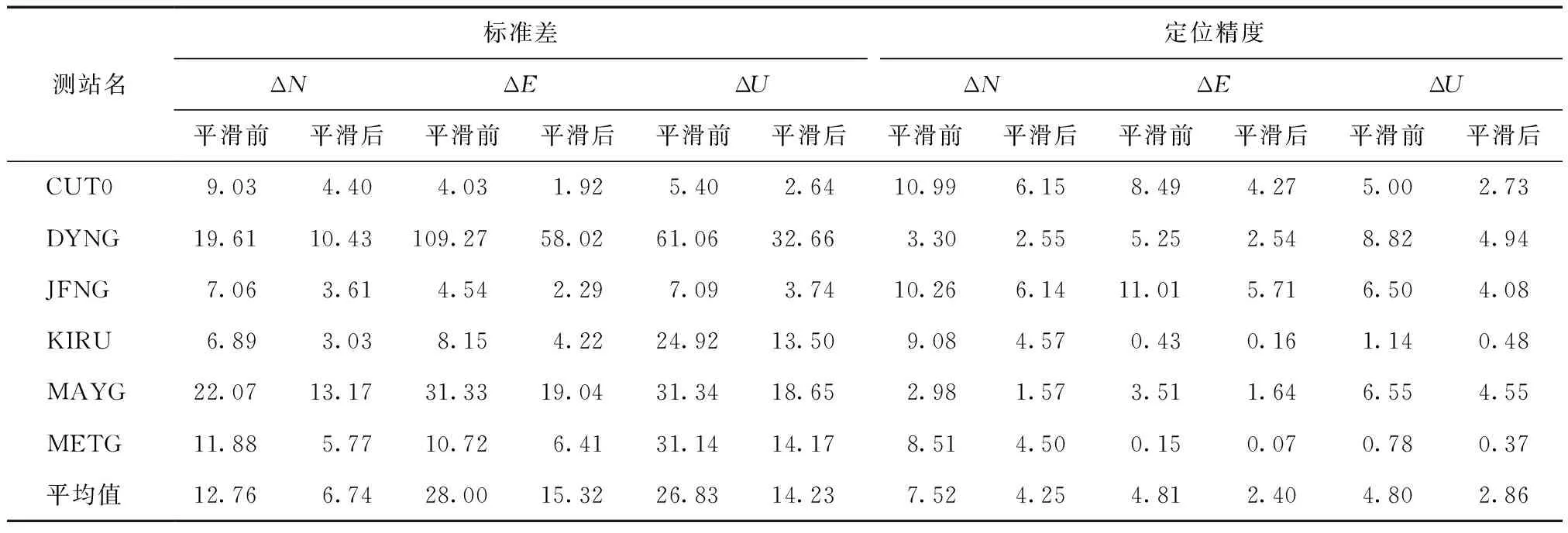
表5 BDS系统各站平滑前后标准差及定位精度对比 m

表6 Galileo系统各站平滑前后标准差及定位精度对比 m

本文还将每天24 h的观测数据按6 h分时段分别进行定位解算，用于分析平滑效果的稳定性。将同一系统下，所有测站每天6 h时段最后一个历元的定位结果偏差绝对值取平均值，作为当天该系统6 h的定位精度指标；同一系统下，所有测站每天6 h时段的标准偏差取平均值，作为当天该系统6 h的滤波标准差。结果如表7～表9所示。

表7 GPS系统6 h时段平滑前后标准差及定位精度对比 m

从表中可以看出，对于6 h时段3个系统的定位结果，平滑后其标准差均有明显减小，定位精度均有较大幅度提高。比较3个系统，其中GPS系统在平滑前水平方向和高程方向上精度优于5 m，各方向标准差在2 m以内，滤波结果稳定，明显的跳跃少，定位精度最高；BDS系统标准差最大，结果稳定性较差，滤波波动大；Galileo系统水平方向上精度优于BDS系统，高程方向上精度更差，整体结果稳定性优于BDS系统。统计平滑后3个系统2项指标变化的百分比如图7所示。

表8 BDS系统6 h时段平滑前后标准差及定位精度对比 m

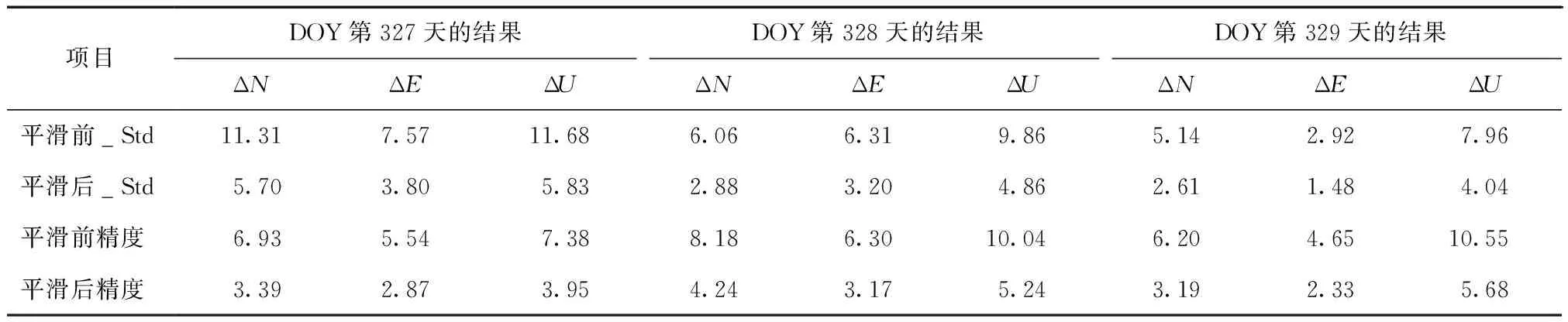
表9 Galileo系统6 h时段平滑前后标准差及定位精度对比 m

图7 3个系统连续30 d平滑前后标准差及定位精度变化

比较连续1个月的平滑效果，3个系统平滑后的标准差减小率和定位精度提高率都非常稳定，说明平滑对定位结果的影响随时间变化具有一定的稳定性和延续性。

3 结束语

本文以双频载波相位平滑伪距原理为依据，分析对比了GPS、BDS、Galileo系统卫星可见数量、载波相位平滑伪距前后定位结果的收敛速度和精度。实验采用6个MGEX站多天的实测数据和精密星历及钟差文件，分别进行了伪距单点定位和载波相位平滑伪距单点定位解算，得出了以下结论：

1)GPS系统可见卫星数量最多，所有测站3 d的平均可见数量接近10颗；Galileo系统所有测站3 d的平均可见卫星数量在4颗以上；BDS系统在一些欧洲测站的可见卫星数量较少，影响其系统的定位结果。

2)3个系统的定位滤波收敛速度经平滑后均有所提高，未收敛的滤波经平滑后能够收敛。其中GPS系统提升最明显，部分测站定位滤波经平滑后所有历元坐标偏差绝对值均小于阈值。对比3个方向可知，N方向上收敛速度提升最明显。

3)平滑能明显提高滤波结果的定位精度，减小其标准差；GPS、BDS、Galileo系统的定位精度分别提高了1.75、1.79、1.84倍；平滑后，滤波结果稳定性更好，明显的跳跃和波动减少，Galileo系统各方向上的标准差均能减小50 %以上；将观测数据按6 h分时段解算，分析连续1个月的解算结果，发现平滑效果具有很好的稳定性和延续性。

[1] HATCH R.The synergism of GPS code and carrier measurements[C]//Defense Mapping Agency and National Ocean Survey.Proceedings of the 3rd International Geodetic Symposium on Satellite Doppler Positioning.Las Cruces，New Mexico：Physical Science Laboratory of the New Mexico State University，1982：1213-1232.

[2] 陈思.一种双频载波相位平滑伪距算法的分析与实现[J].科技信息，2010(23)：945-946.

[3] 赵胜，魏亮，段召亮.GNSS接收机的伪距平滑技术研究[J].无线电工程，2010，40(4)：32-34.

[4] 李朋，徐博，刘文祥，等.基于载波相位平滑伪距的卡尔曼滤波定位方法[J].全球定位系统，2013，38(4)：16-19.

[5] 唐卫明，刘智敏.GPS载波相位平滑伪距精度分析与应用探讨[J].测绘地理信息，2005，30(3)：37-39.

[6] 胡耀坤，王伟，李斌.北斗多频载波平滑滤波的运用[C]//中国卫星导航系统管理办公室学术交流中心.第四届中国卫星导航学术年会论文集.北京：中国卫星导航系统管理办公室，2013：6-10.

[7] 隋叶叶，杨小江，柳涛.载波相位平滑伪距算法研究与精度分析[J].电子设计工程，2013，21(8)：112-115.

[8] 李岑，黄智刚，王曙阔，等.载波相位平滑伪距在GPS单点定位中的应用[C]//中国卫星导航系统管理办公室学术交流中心.第二届中国卫星导航学术年会论文集.北京：中国卫星导航系统管理办公室，2011：7-12.

[9] 刘斌，王园，李志刚.北斗单频相位平滑伪距精度分析[J].测绘技术装备，2014，16(3)：94-96.

[10] 刘瑞华，杨兆宁，詹先龙.北斗系统载波相位平滑伪距研究[J].中国民航大学学报，2012，30(3)：28-31.

[11] 范士杰，孔祥元.基于Hatch滤波的GPS伪距相位平滑及其在单点定位中的应用[J].勘察科学技术，2007(4)：40-42.

[12] 刘俊，何秀凤，张文晓.采用相位平滑伪距方法研究两种卫星导航系统组合定位的精度[J].导航定位学报，2013，1(4)：11-13.

[13] 刘长建.GNSS电离层建模方法与质量控制研究[D].郑州：信息工程大学，2011：24-28.

[14] 李征航，赵晓峰，蔡昌盛.全球定位系统(GPS)技术的最新进展第五讲：利用双频GPS观测值建立电离层延迟模型[J].测绘地理信息，2003，28(1)：41-44.

[15] 王旭峰.基于GPS/BDS导航系统电离层建模研究[D].徐州：中国矿业大学，2016：12-17.

[16] ESA.Galileo begins serving the globe[EB/OL].(2016-12-15)[2017-01-01].http：//www.esa.int/Our_Activities/Navigation/Galileo_begins_serving_the_globe.html.