GPS广播星历轨道误差分布模型探讨

刘瑞宁，李建文，郭亮亮，刘德智

(1.信息工程大学/北斗导航应用技术河南省协同创新中心，郑州 450001；2.贵州省水利水电勘测设计研究院，贵阳 550000)

0 引言

随着全球卫星导航系统(global navigation satellite system，GNSS)的迅速发展，导航定位技术在诸多科研和生产领域得到了广泛的应用；人们对导航系统性能的要求越来越严格：开展对导航系统服务性能的监测评估研究十分必要。文献[1]详细给出了监测评估的主要研究内容与方法，并提出了一种基于卫星轨道长期演化特点来确定监测范围的方法。文献[2]对星历误差进行了评估并分析了相关评估手段，通过实测GNSS数据，对目前四大系统的广播星历进行了评估与数据分析。目前已有大量文献对广播星历精度评估展开研究，但关于广播星历的轨道误差分布模型的研究相对较少[3-5]，而轨道误差分布模型的确定是开展GNSS导航电文的实时监测的基础和前提。

本文提出一种利用精密星历来计算广播星历轨道误差的算法，并对轨道误差的分布模型进行假设检验，最终确定轨道误差所服从的分布模型。

1 基本计算模型

1.1 广播星历

全球定位系统(global positioning system，GPS)广播星历中包含了6个轨道根数及9个摄动参数和其他参数，而利用广播星历计算瞬时历元t时刻的卫星位置的具体方法也在众多文献中有所介绍[6-7]。

1.2 精密星历

国际GNSS服务组织(International GNSS Service，IGS)精密星历给出的卫星的位置精度优于5 cm，相对于广播星历而言，事后精密星历可以视作真值。当要计算其他时刻的钟差与卫星坐标时，可以采用内插的方法。而关于精密星历拟合轨道的插值方法，已有学者进行过研究比较，常见的是拉格朗日多项式插值法[8-9]。

1.3 轨道误差计算模型

据前所述，可求得由广播星历计算得出的实时轨道位置和由精密星历拟合的真实的轨道位置，从而可求出轨道误差，其表达式为

(VX,VY,VZ)T=(X1,Y1,Z1)T-(X2,Y2,Z2)T

(1)

式中：(X1,Y1,Z1)T为由精密星历拟合的真实的卫星轨道3维位置；(X2,Y2,Z2)T为由广播星历计算得出的实时卫星轨道3维位置；(VX,VY,VZ)T为轨道X、Y和Z方向误差。值得注意是在计算轨道误差时，参考框架、卫星相位中心与时空基准应相一致，否则将直接影响轨道误差值的正确与否[10]。

2 误差分布模型检验

2.1 常见假设检验

1)χ2拟合检验法。χ2(即卡方)拟合检验就是统计样本的实际观测值与理论推断值之间的差异，观测值与理论值之间的差异与卡方值是正相关的，差异越小卡方值越小，反之卡方值越大；如果观测值与理论值完全相等时，卡方值为0，表明观测值与理论值完全符合。其详细检验步骤见其他文献[11]，[12]146-151。

2)偏度和峰度联合检验法。由于正态分布的密度曲线是对称且陡缓适中的，可以用偏度和峰度2个数字特征来描述分布密度曲线；其中偏度指密度曲线的偏斜程度，峰度描述的是密度曲线的陡缓程度。若样本来自正态总体，则其经验分布密度曲线既不能偏斜太多又不能陡缓过度；因为对于正态分布而言，偏度为0，峰度为3：因此当样本来自正态总体时，其偏度应接近于0，峰度接近于3[12]158-160。

3)正态概率纸检验法。正态概率纸检验法的基本思路是把正态分布的分布函数转化为概率纸上的线性函数，其过程详见相关文献[12]160-163,[13]。

2.2 实验分析与模型确定

本文实验采用国际GNSS监测与评估系统(international GNSS monitoring and assessment system，iGMAS)分析中心接收的广播星历及IGS事后精密星历，选取2016-01-01 T 00：00到2017-08-24 T 00：00时间段的数据，依据广播星历更新时间，2 h采集1个样本数据。根据第1节中的计算思路可得出检验量即广播星历轨道误差，进而对这些误差样本进行统计分析与假设检验。

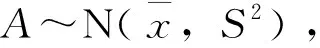
假设检验工具是采用Matlab中所含的检验函数，主要检验函数为正态分布Jarque-Bera检验函数jbtest即偏度与峰度的联合检验、chi2gof检验函数即卡方拟合优度检验、Kolmogorov-Smirnov检验函数kstest、正态分布概率纸检验normplot。其中第4种属于绘图检验。

按照卫星的类型(IIF、IIR、IIR-M)分别选取G03、G07、G12、G18、G19、G24 6颗卫星作为例证数据来进行检验。其中G03和G24为IIF型卫星，G18和G19为IIR型卫星，G07和G12为IIR-M型卫星。

经过实验分析对样本数据进行统计，得出基本的特征数字如表1所示。

表1中VX、VY和VZ分别表示轨道X方向误差、Y方向误差和Z方向误差。从表1中可以看出，轨道误差的均方根(root mean square，RMS)均在合理范围以内[14]。

根据轨道误差数据的基本特征，采用均值和标准差作为参数进行分布拟合的检验，即检验是否服从正态分布和T分布。检验结果如表2所示。

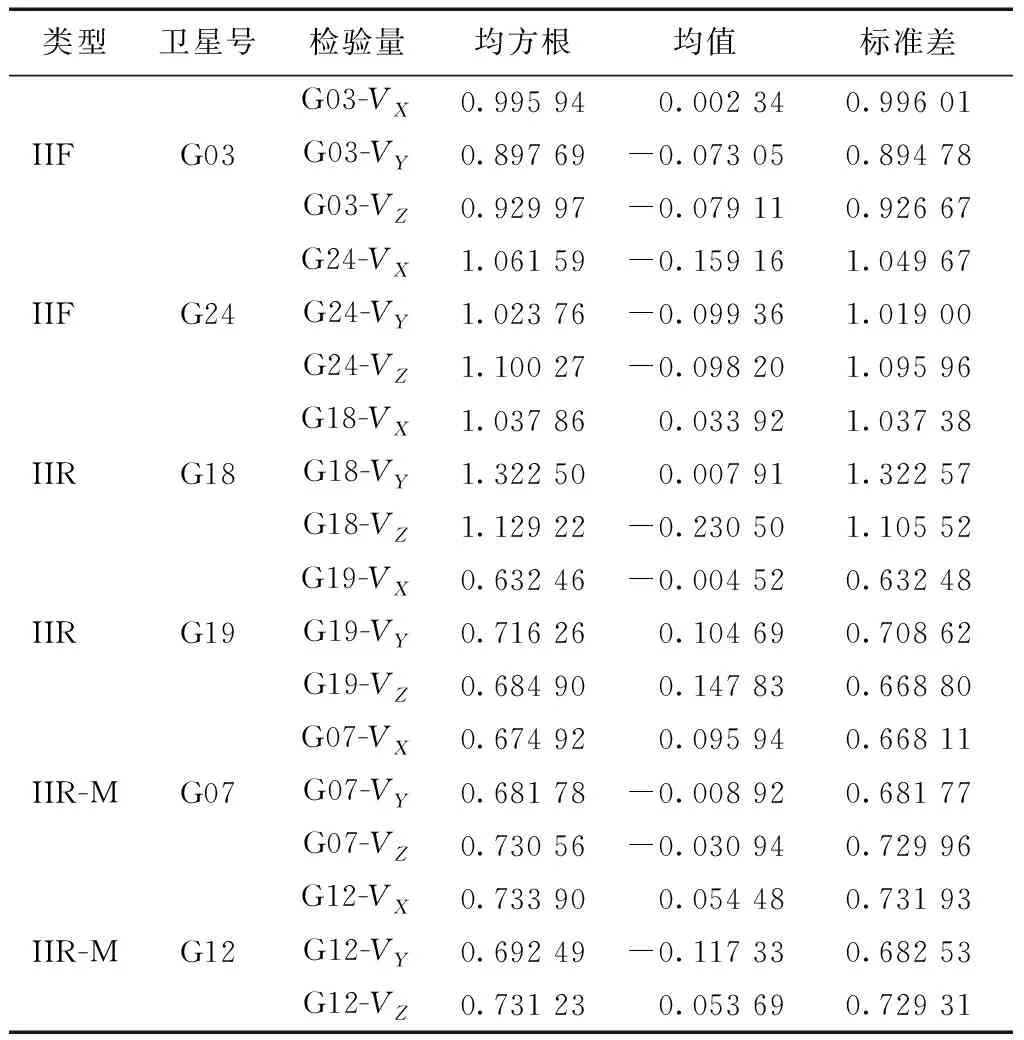
表1 轨道的误差统计信息 m

表2中“0”表示肯定，即样本服从假定分布；“1”表示否定，即样本不服从假定分布。从表中可以看出：误差样本不服从T分布；而且大部分样本也不服从正态分布，只有个别样本服从正态分布。

本文还对所有样本进行了直方统计和正态概率纸检验，这样不仅可以有另一种结果作为辅助判断，更能直观显示数据的分布形态。检验结果见图1～图6，每一幅大图中有6幅小图，其中图(a)、图(b)、图(c)分别为轨道X、Y和Z方向误差的直方统计，图(d)、图(e)、图(f)分别为轨道X方向、Y方向和Z方向误差的正态概率纸检验。直方统计图中：横坐标为样本值；纵轴为频次，即在该区间段样本出现的次数；

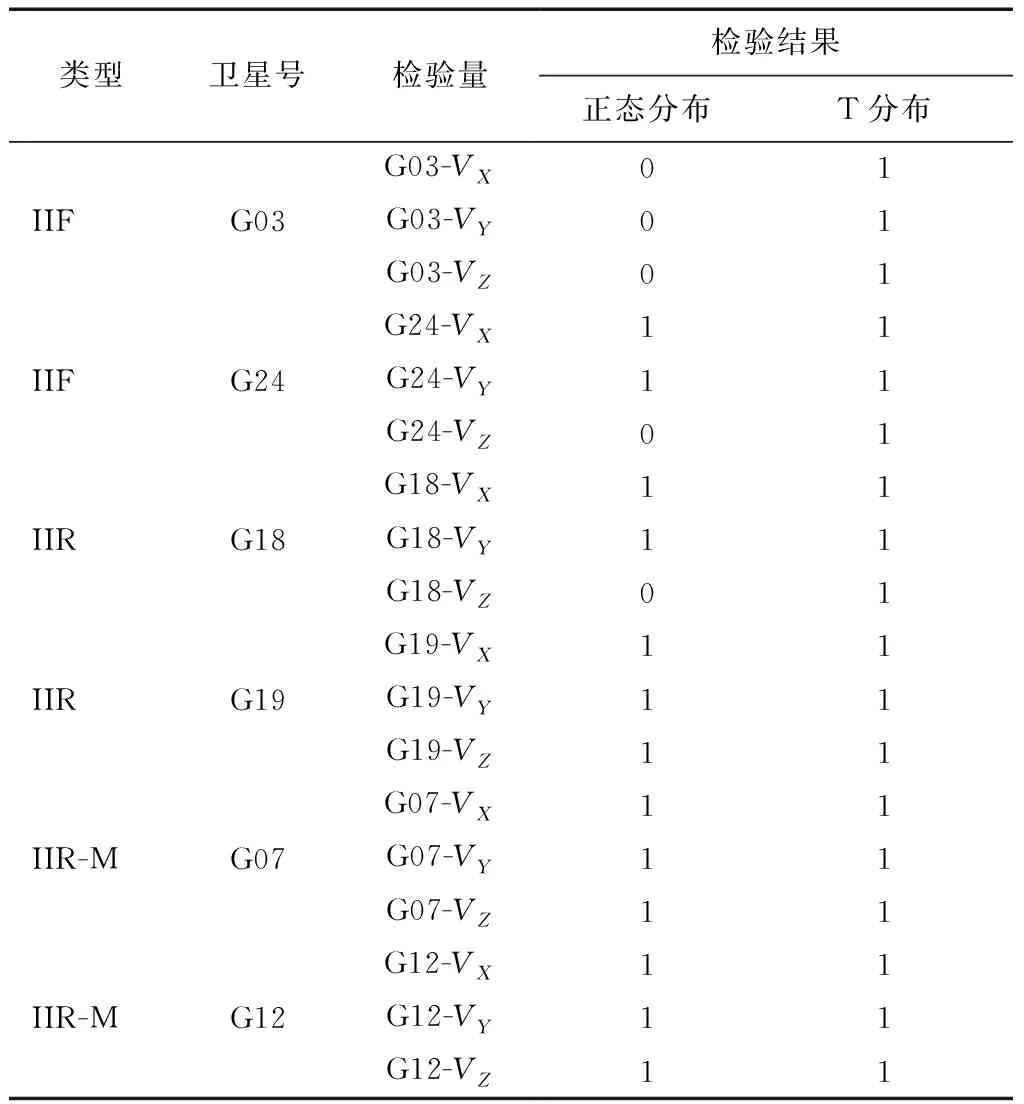
表2 轨道误差检验结果

拟合曲线为适应该样本数据的正态分布曲线。正态纸检验图中：横坐标表示样本值，纵坐标表示百分位数，直线为参照线，星形点为数据点；当样本数据服从正态分布时，样本值所对应的百分位数就会越来越靠近参照线从而形成一条近似的直线，否则就会越来越偏离渐近线形成曲线。

从图中可知：G03、G07、G12、G19、G24轨道误差最近似服从正态分布，而G18(图5)的轨道误差分布呈明显的双峰特征。而当直方图出现双峰特征时，可以推断是由于样本值来自2个总体、2个分布的数据混合。

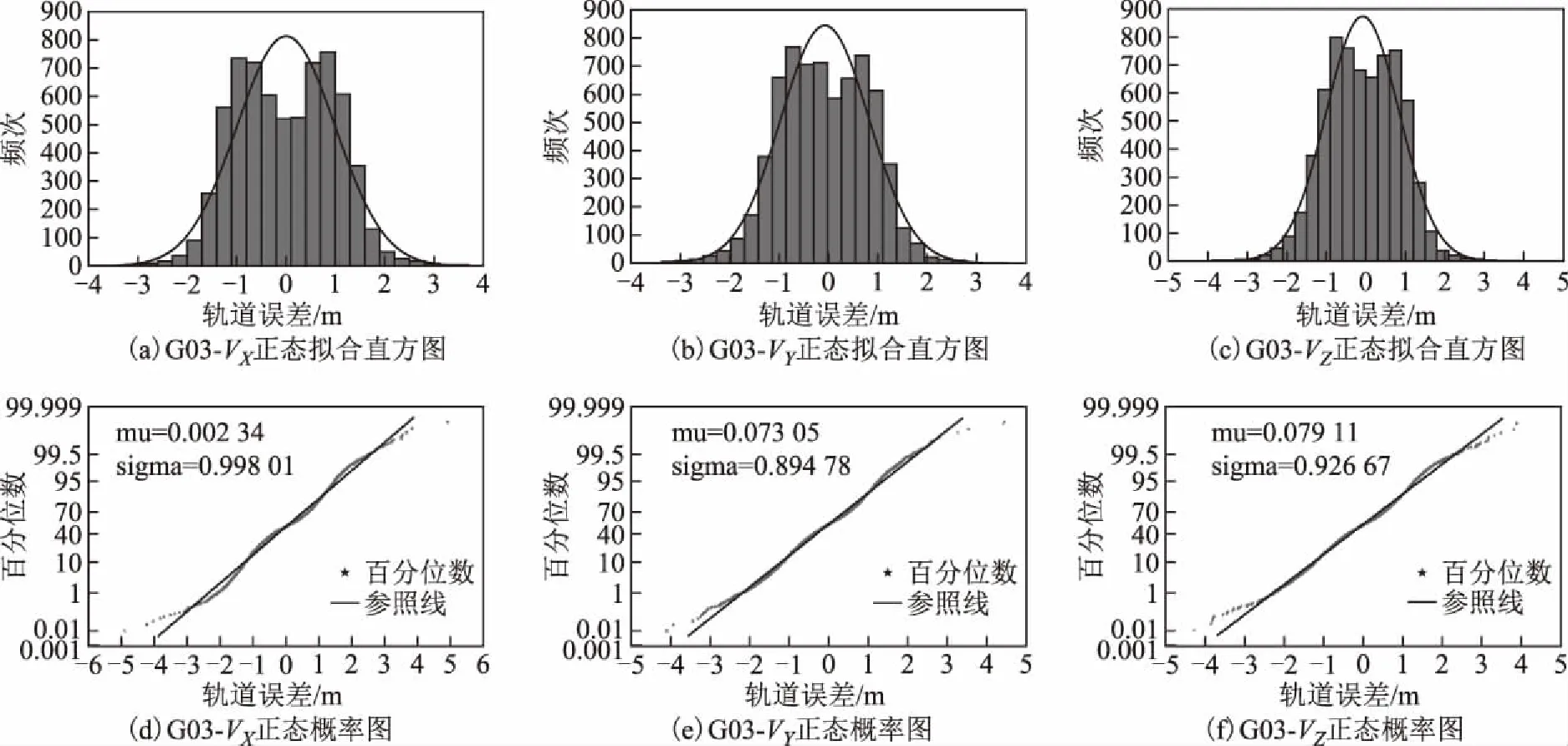
图1 G03轨道误差直方统计与正态概率纸检验

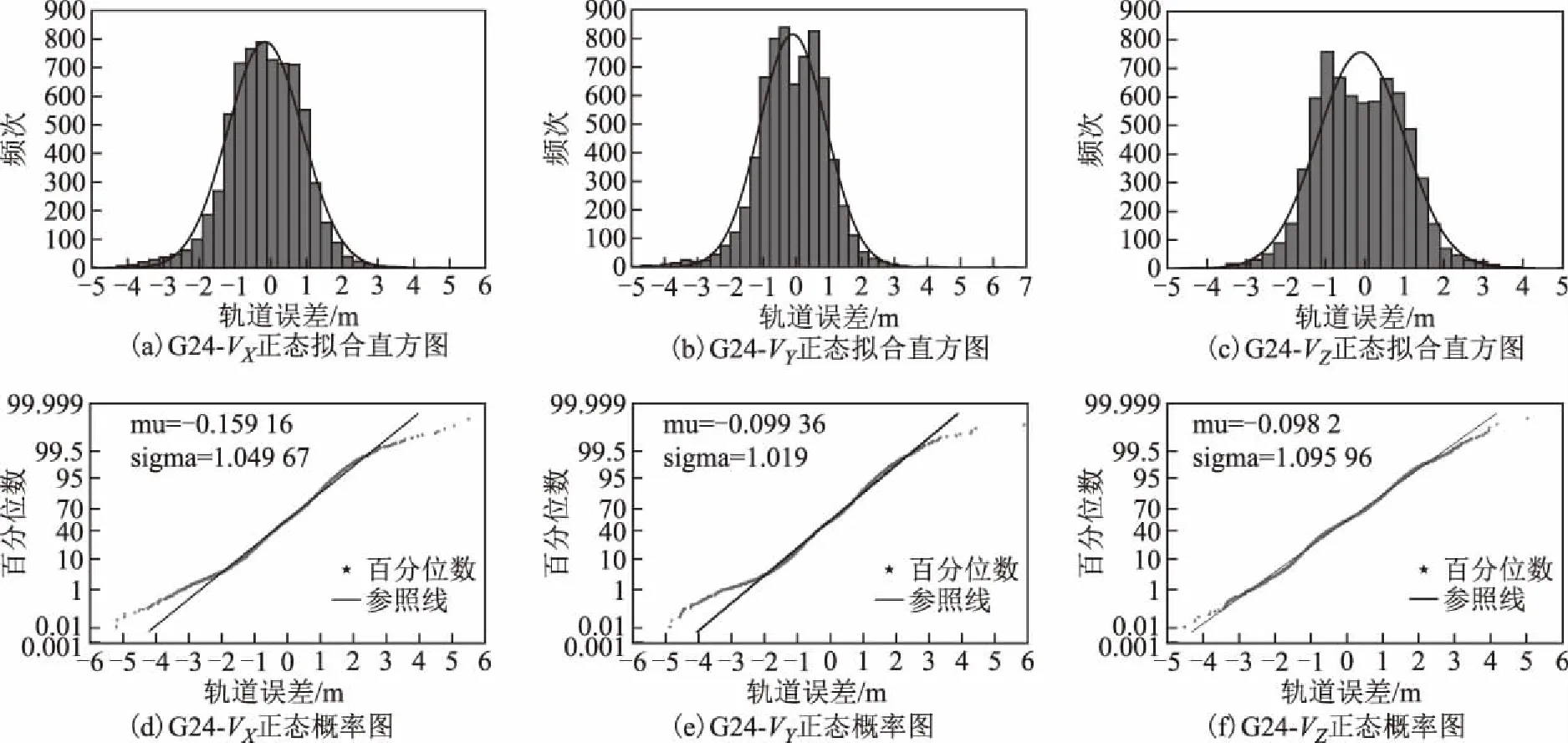
图2 G24轨道误差直方统计与正态概率纸检验

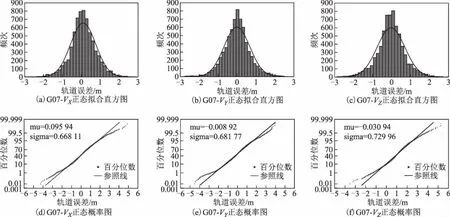
图3 G07轨道误差直方统计与正态概率纸检验

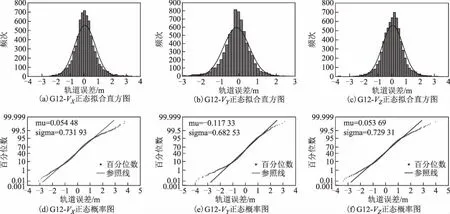
图4 G12轨道误差直方统计与正态概率纸检验

图5 G18轨道误差直方统计与正态概率纸检验

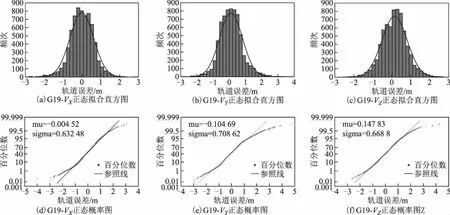
图6 G19轨道误差直方统计与正态概率纸检验

2.3 具有双峰特征的误差分布检验

对于具有双峰特征的G18的轨道误差，根据双峰分布的基本理论对轨道误差呈现双峰分布特征的数据进行分段拟合检验，分别对2段样本数据进行正态分布、T分布以及Weibull分布检验。根据轨道误差数据的基本特征，均值取值都在0附近，所以取分界值为0。其中Weibull分布检验只检验样本值大于0时的样本总体；这是因为Weibull分布的变量取值区间需在[0,+)，检验所需的形状参数和比例参数根据样本值进行拟合。而两侧的样本分布在总的双峰分布中所占的比重也由两侧数据量所占的比值决定[15-16]。

重复2.2节检验过程，得出结果如表3和图7～图9所示。从结果可知，正负两侧的数据均近似服从正态分布，据此可以推断出G18轨道误差最近似服从的分布是由2个正态分布组成的双峰分布。

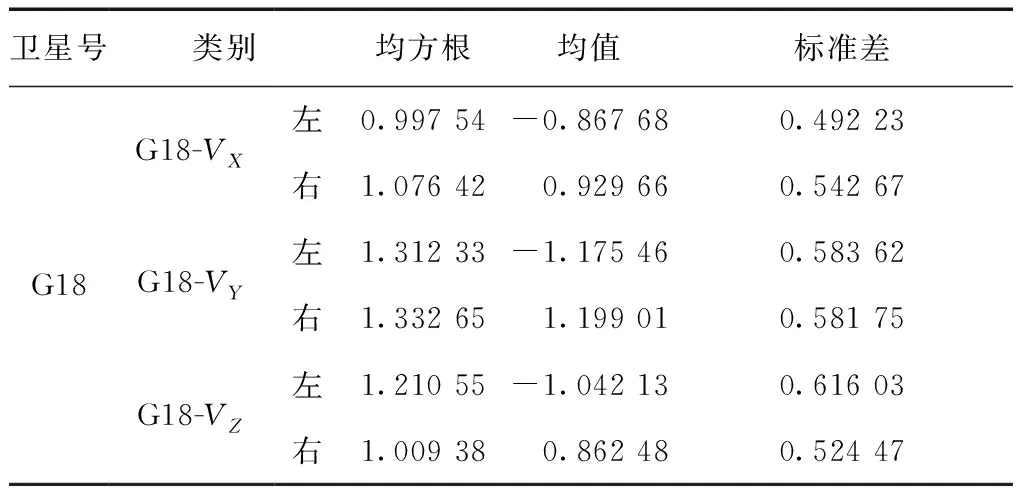
表3 具有双峰分布特征的轨道的误差统计 m

图7 G18轨道X方向误差直方统计与正态概率纸检验

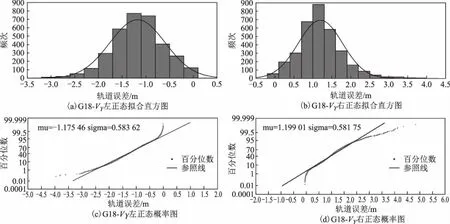
图8 G18轨道Y方向误差直方统计与正态概率纸检验

图9 G18轨道Z方向误差直方统计与正态概率纸检验

另外，除了以上例证的卫星，本文还检验了所有其他的GPS在轨卫星，发现除了G18的轨道误差具有双峰分布特征外，G11、G13、G14、G18、G20、G28的轨道误差具有同样的分布特征，而这些卫星均为IIR星。

3 结束语

监测评估工作是评价和确保卫星导航系统服务性能的有效手段。本文主要分析了以精密星历为基准的GPS广播星历的轨道误差，并对这些误差进行拟合分布检验。从分析结果来看，卫星的轨道误差(X、Y、Z方向)出现了多样性：其中IIF星和IIR-M星及个别IIR星的误差分布模型最近似服从以均值和标准差为参数的正态分布；大部分IIR星的误差分布模型呈现双峰特征，且是服从由2个正态分布混合而成的双峰分布。当轨道误差呈双峰分布时，如何更精准地对广播星历进行监测与评估是下一步的研究工作。

致谢：感谢iGMAS信息工程大学分析中心(LSN)给予的帮助和支持。

[1] 张清华.GNSS监测评估理论与方法研究[D].郑州：信息工程大学，2014.

[2] 刘帅.卫星导航系统空间信号精度评估理论与算法研究[D].郑州：信息工程大学，2016.

[3] 张耀文.GPS广播星历及其精度评估研究[D].西安：长安大学，2007.

[4] 陈永就.GNSS广播星历的精度评定[J].测绘与空间地理信息，2015，38(6)：186-191.

[5] MONTENBRUCK O，STEIGENBERGER P，HAUSCHILD A.Broadcast versus precise ephemerides：a multi-GNSS perspective[J].GPS Solutions，2015，19(2)：321-333.

[6] 刘磊，盛峥，王迎强，等.利用广播星历计算GPS卫星位置及误差分析[J].理工大学学报(自然科学版)，2006，7(6)：592-596.

[7] 王俊杰，许杭，高俊强.基于广播星历改正实时精密星历与钟差获取研究[J].全球定位系统，2015，40(5)：21-25.

[8] 张养安，李俊锋，薛兆元，等.IGS精密星历和钟差的算法比较研究[J].地理信息世界，2016，23(4)：45-49.

[9] 吴继忠，高俊强，李明峰.IGS精密星历和钟差插值方法的研究[J].工程勘察，2009，37(7)：52-54.

[10] 郭斐，张小红，李星星，等.GPS系列卫星广播星历轨道和钟的精度分析[J].武汉大学学报(信息科学版)，2009，34(5)：589-592.

[11] 沈宏峰，陈群.实用的卡方检验法[J].微型电脑应用，1997(5)：61-63.

[12] 庄楚强，何春雄.应用数理统计基础[M].3版.广州：华南理工大学出版社，2006.

[13] 岳鹏，朱坤平.基于随机模拟方法对正态概率纸检验的改进[J].统计与决策，2017(3)：14-16.

[14] 王霞迎，秘金钟，张德成，等.GPS广播星历位置、速度和钟差精度分析[J].大地测量与地球动力学，2014，34(3)：164-168.

[15] 徐鑫，郭民之，石峰利.双峰数据分布的模拟[J].云南师范大学学报，2013，33(2)：46-51.

[16] 冯祖德，涂铭旌，鄢文彬.韧性值呈双峰分布时参数的统计推断问题的探讨[J].理化检验：物理分册，1992，28(5)：30-32.