一种无误差的捷联惯导数值更新新算法
2018-06-07严恭敏杨小康秦永元
严恭敏,杨小康,翁 浚,秦永元
(西北工业大学 自动化学院,西安 710072)
0 引言
自二十世纪六七十年代开始,捷联惯导的传统算法经过了几十年的发展,其主流设计方法及细节已经完成[1-6]。姿态更新是整个捷联算法的核心,为了补偿姿态不可交换误差,基于等效旋转矢量概念提出了多子样及其优化算法;利用对偶性原理,可以直接将姿态多子样算法应用于速度更新算法[7];与前两者相比,位置更新算法的算法误差影响相对较小些,在许多应用中一般可以不予考虑。
然而,传统的不可交换误差补偿多子样算法是在等效旋转矢量方程(Bortz方程[3])进行二阶近似的基础上推导的,它本质上存在原理性误差,特别在大机动环境下计算误差不容忽略,有时高子样算法的误差反而比低子样的大[8]。即使考虑得更加周全,保留Bortz方程的高阶近似[9],也还依然存在原理性误差,且高阶补偿算法的推导过程会变得非常复杂。最近,一些学者研究了无原理性算法误差的捷联姿态更新方法,彻底解决了大机动环境下的姿态更新问题[10-11]。
本文根据捷联惯导的姿态阵、速度和位置微分方程,直接采用泰勒级数展开方法,给出了全套捷联惯导更新数值算法,在陀螺输出角速度和加速度计输出比力满足多项式形式假设的条件下(根据数学知识,平滑的角运动或线运动总是可以用多项式无限逼近的),该算法不存在任何原理性误差,隐含了对姿态、速度和位置更新不可交换误差的完美补偿。通常在地球表面上实施的惯性导航需同时考虑地球自转和有害加速度的补偿,相对于大机动而言这些补偿量均为缓变量,计算误差很小。为了理论研究和对比分析方便,暂且以惯性坐标系作为导航参考系,给出了简洁的捷联惯导数值更新算法,最后,通过仿真实验验证了算法不存在原理性误差,具有很高的计算精度。
1 由角增量(速度增量)拟合角速度(比力)的方法
捷联惯导系统中的惯性器件通常是角增量(或速度增量)输出形式的,本文的算法要以角速度(或比力)作为输入,为此,先给出由角增量(速度增量)转换为角速度(比力)的计算方法。
由文献[12]知,若陀螺角增量的采样间隔为h,在时间段(-ph,nh]内进行了N次采样(p,n均为整数,p≥0,n>0且p+n=N),角增量分别记为Δθj(j=-p+1,-p+2,…,n),则可得角速度ω的关于时间t的(N-1)次多项式拟合为
(1)
式中:
同理,可得比力f的多项式拟合为
(2)

2 捷联惯导更新新算法的推导
首先给出两矩阵之乘积的求导公式,即若Z=XY,则有
(3)
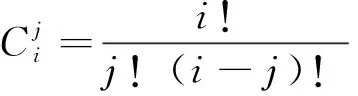
接下来根据捷联惯导姿态阵、速度和位置微分方程分别给出相应的数值更新算法。
1)在捷联惯导算法中,姿态阵微分方程为

(4)
式中:C为姿态矩阵;(ω×)表示由向量ω构成的反对称阵。
假设姿态更新时间间隔为(0,T]且T=nh,将T时刻的姿态阵CT在0时刻展开成泰勒级数形式,并将式(4)代入,可得

(5)
根据式(3)和式(4),有

(6)

2)捷联惯导速度微分方程为

(7)
将T时刻的速度VT展开成泰勒级数形式为
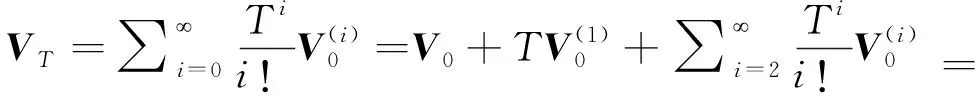
(8)
根据式(3)和式(7)有
(9)
式(8)右端的第三项(求和项)也隐含了对速度不可交换误差(划船误差)的精确补偿。
3)捷联惯导位置微分方程为

(10)
将T时刻的位置PT展开成泰勒级数形式为

(11)
式(11)右端的第三项(求和项)隐含了对位置不可交换误差(涡卷误差)的精确补偿。
至此获得完整的包含姿态阵更新、速度更新和位置更新的全套捷联惯导数值更新算法,其计算流程可总结如图1所示。算法以0时刻的姿态阵C0、速度V0和位置P0,以及陀螺角增量Δθj和加速度计速度增量ΔVj为输入,经过迭代求导与累加求和后,输出T时刻的姿态阵CT、速度VT和位置PT。当角速度ω和比力f可以用多项式描述且泰勒级数展开项数足够多时,理论上算法误差仅取决于计算机的数值计算精度,全套算法不存在任何原理性误差。
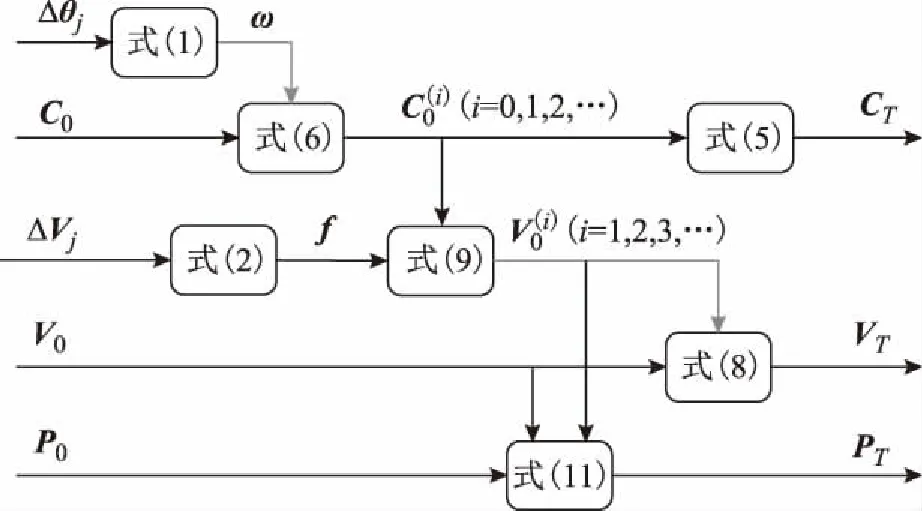
图1 算法更新流程
3 仿真验证
假设飞机做类似于“普加乔夫眼镜蛇机动”的飞行动作[13],捷联惯导输出的角速度ω和比力f可用二次多项式描述,在载体坐标系下按“x(右)—y(前)—z(上)”顺序表示的多项式系数矩阵分别为
(12)
(13)
式中:角速度ω的单位为rad/s,比力f的单位为m/s2。显然,飞机只在x轴方向上有角速度机动,而在y轴和z轴方向上均有加速度机动,飞机的飞行轨迹始终在同一铅垂面上。
设置惯性传感器采样频率100 Hz,仿真时长1 s,飞机初始姿态为0,速度300 m/s。经过传感器数据生成和捷联惯导更新解算仿真,本文新算法与传统多子样算法相比,在1 s时导航速度误差如表1所列。

表1 算法误差比较 m/s
由表1可见,由于同时存在强烈的角速度和加速度机动耦合,传统算法的速度误差较大,高子样算法的误差反而大于低子样算法,其中4子样算法的z轴速度误差超过了0.1 m/s。然而对于新算法而言,其速度误差非常小,几乎可以忽略不计,近似为0。
4 结束语
由于精确的Bortz方程非常复杂,不便于直接应用,在传统的姿态不可交换误差补偿多子样算法推导过程中,必须对Bortz方程进行简化,忽略高阶项的影响,从而使得传统的多子样补偿算法总是近似成立的,特别在大机动环境下容易引起较大的原理性误差。本文放弃了求解一组固定的不可交换误差补偿系数的做法,直接采用泰勒级数展开式求解捷联惯导姿态阵、速度和位置的数值更新算法,从推导过程中可以看出,当陀螺角速度和加速度计比力能用多项式形式描述时,新算法不存在任何原理性误差,仿真实验结果也表明了新算法是无误差的。就目前的计算机运算能力而言,类似于文献[10]的分析,新算法的计算量是可以接受的。当然,在本文理论推导的基础上,读者通过一些简单的修改即可扩展成指北方位捷联惯导系统的数值更新算法,实现高精度的导航解算。
[1] SAVAGE P G.A new second-order solution for strapped-down attitude computation[EB/OL].[2017-10-28].http://www.ijicic.org/ijicic-12-08014.pdf.
[2] JORDAN J W.An accurate strapdown direction cosine algorithm[EB/OL].[2017-10-28].https://www.researchgate.net/publication/24331776_An_accurate_strapdown_direction_cosine_algorithm.NASA TN-D-5384,1969,9.
[3] BORTZ J E.A new mathematical formulation for strapdown inertial navigation[J].IEEE Transactions on Aerospace and Electronic Systems,1971,7(1):61-66.
[4] MILLER R.A new strapdown attitude algorithm[J].Journal of Guidance,Control,and Dynamics,1983,6(4):287-291.
[5] PARK C G,KIM K J,LEE J G,et al.Formalized approach to obtaining optimal coefficients for coning algorithms[J].Journal of Guidance,Control,and Dynamics,1999,22(1):165-168.
[6] SAVAGE P G.Strapdown inertial navigation integration algorithm design part 1:attitude algorithms[J] Journal of Guidance,Control,and Dynamics,1998,21(1):19-28.
[7] ROSCOE K M.Equivalency between strapdown inertial navigation coning and sculling integrals/algorithms[J]. Journal of Guidance,Control,and Dynamics,2001,24(2):201-205.
[8] 严恭敏,严卫生,徐德民.经典圆锥误差补偿算法中剩余误差估计的局限性研究[J].中国惯性技术学报,2008,16(4):379-385.
[9] WANG M S,WU W Q,WANG J L,et al.High-order attitude compensation in coning and rotation coexisting environment[J].IEEE Transactions on Aerospace and Electronic Systems,2015,51(2):1178-1190.
[10] 严恭敏,翁浚,杨小康,等.基于毕卡迭代的捷联姿态更新精确数值解法[J].宇航学报,2017,38(12):1307-1313.
[11] 武元新,郁文贤.一种基于函数迭代积分的刚体姿态解算方法:201710273489.3[P].2017-11-10.
[12] 严恭敏,杨小康,翁浚,等.一种求解姿态不可交换误差补偿系数的通用方法[J].宇航学报,2017,38(7):723-727.
[13] 李中华.Su—27飞机眼镜蛇机动及其战术意义[J].飞行力学,2000,18(1):54-57.
