谈新课程标准下的“变式教学”
2018-06-06孙光云
孙光云
(甘肃省临夏县土桥中学 731801)
现行的数学课本只为学生学习数学知识提供了一个平台和资源,而对不同地域,不同基础水平的学生而言,不可能完全适合.对教师和学生而言,这是一个现实的困难.另一方面,依据新课程标准,学生需要在学习中对课本的基础知识和基本技能做到举一反三,直到不同程度的应用.而要克服这个困难和实现课标的这一要求,我认为数学“变式教学”的方法是十分有效的手段.
变式就是改变事物的非本质特征,以便更好地认识事物的本质特征的一种方法.所谓“变式教学,就是指教师在具体教学环境中,依据知识点的特征和学生的实情有目的对命题进行适合需求的变形或变换载体的做法.变式教学法,它的本质是设置一系列适合研究知识点需求的变式,来展现数学问题的发现和认识的过程;知识的理解和掌握的过程;问题的转换和解决的过程,从而达到提高学生学习效果的一种课堂模式.下面就以教学均值不等式内容时设计的片段为例谈谈对变式教学法的实际运用.

这是对均值不等式的条件、结构特征、取等号条件的基本测试,是对均值不等式运用的开始.为了进一步熟练用均值不等式求最值,我设计了如下变式教学:

这题比上一题有所上升,“积”尽管是定值,但项不为“正”,学生只有构造正项才能运用均值不等式.

这题需要分类讨论,需要思维的严密性.

这题“正”是明显的,但“积”不是定值,需要构造“积”为定值,即需要创新.学生只有对已有结构特征认真观察分析的基础上,才能找到添项后减项的方法,即减1加1.

依据上题的经验,学生容易构造“积”为定值,项为“正”,很“容易”算得“最小值”,也很“容易”发生争论,这是需要的.只有经历了这个思维过程,学生才会强化对“相等”的认识.
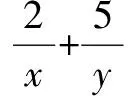
这个问题既涉及到对数的性质,又用到均值不等式;既要找到定值,又要构造定值.
变式6:做一个体积为32m3,高为2m的长方体纸盒,底面的长与宽取什么值时用纸最少?
本题要求学生分析问题,建立模型,解决问题.
变式7:仿照以上“变式”,构造一个“变式”能用均值不等式求最值.
这个看似宽泛的问题,实际上是为了创新的设置,是实现本节课的最高目标的有效手段.
从以上教学片段不难发现,变式教学法具有以下优势:
运用变式教学有利于提高课堂教学效果.变式教学变换问题的条件和结论,改变问题的形式和载体在一定程度上可以激发思维的灵活性和主动性,从而可以更深刻地理解课堂所学内容.变式教学像小块切香肠,学生品尝到了容易吃到的香肠香味,才会有品尝下一块,甚至更多块的欲望.这样学生就有了学习的主动性,有了学习的主动性,学生才能积极参与到学习活动中,而为了保持这种主动性,我们再设计学生能品尝到的更美味的变式.学生在不断成功中前进,课堂教学效果不提高是不可能的.
运用变式教学有利于提升学生学好数学的能力.现代教学理念的共识是:扎实的基本功和良好的思维品质是学好数学的必备条件,而兴趣是催化剂.变式教学可根据学生实际,灵活设计变式,能做到对症下药.学生在不断的变式活动中,不但能强化基础知识,而且能培养学生思维的灵活性和严密性.如上面均值不等式的变式教学,它既有灵活性的训练,也有对均值不等式运用严密性的培养.实例中的一题多变,给人一种新颖、生动的感觉,特别是变式6和变式7能唤起学生大脑思维的主动性,从而能够产生主动参与到学习活动中的动力,保持学生参与课堂活动的兴趣和热情.由此可见,变式教学对提升学生学习能力成效显著.
运用变式教学有利于培养学生的创新能力.我们在数学学习中把旧的知识,通过新的组合,得出新的结果;把已有的结论,借用新的载体,表示出来;常见的结论,经过观察分析,用到全新的问题中,都是创新的举措.培养创新能力的前提是抓好学生的双基,关键是要有问题意识.学生有技能, 有疑问,才能去思考,才会有创新的机会.例如变式1到变式4是从多角度,多侧面,多方位训练双基的过程.变式5到变式7,不但为学生提出了疑问,激发了学生学习的兴趣,而且为学生提供了适宜创新的环境,使创新成为可能.
从以上教学片段我们很容易体会到:变式教学为了能做到使优、良、中差的学生各有所得,都能体会到成功的乐趣,并激发学生的学习热情,达到举一反三、触类旁通的效果,课堂教学设计应注意以下两点:
教学设计要具有针对性,切忌死板硬套.变式设计既要考虑学情,也要考虑所学知识的特征.例如上面实例中设置的变式,面对的学生基础就比较薄弱,变式的起点和台阶都比较低;同时,变式1到变式4是以均值不等式的知识特征从不同角度针对性设计的.设计中,切忌不顾学情而照搬照抄所谓成熟的变式设计.
教学设计要具有适合性,切忌高低不分.变式要遵循学生认知规律,要从易到难,由浅到深,由已知出发,一小步一小步变式 ,步步都要有提升.因为过于简单的变式题对学生来说是重复劳动,对学生思维的品质得不到很好的磨炼;难度太大的变式容易挫伤学生学习的积极性,达不到预期的教学效果,所以变式前要弄清学情,依据学情设计变式.如:以上变式实例适合农村普通高中平行班学生,对城市高中学生就不行了.因此要根据学生认知规律和所教学生的学情,设计适合的变式至关重要.
总之,高中教师要不断更新教学观念,因材施教,继续完善好“变式”教学模式.用“老坛”装“新醋”,最终达到提高教学质量的目的,为学生学好数学、用好数学打下坚实的基础.
参考文献:
[1]胡惠阁.谈高考数学复习中的变式与拓展[J].中学教学参考,2011(04).
[2]潘勇.数学变式题的构造及其教学[J].上海中学数学,2011(Z1).
