参数方程在高中数学解题中的应用探析

单溧莉

(江苏省泰州市民兴实验中学 225300)

数学因其知识点难且多、理性思维强的特点，一直以来都是学生的死穴，很多学生学习成绩提不上去就是败在了数学上.学生之所以数学不好，就是不会做题，没有解题技巧.要想提高高中的教学质量，数学首当其冲.参数方程作为高中数学的重要解题方法在近年来得到了广泛的应用，为学生解决了很多数学难题.它做为高考的常考知识点，在高中数学学习中一直占据较大的比重，而且使用参数方程解题，可以帮助学生更好的理解题目，大大降低了学生解题的难度，对学生解题效率的提高也有很大的帮助.因此，我们教师要抓住参数方程解题的优势，重视对学生参数方程的训练，锻炼学生更多的解题技巧，才能实现数学教学质量的稳步提高.

一、圆的应用

参数方程的使用形式是把x和y列成一个方程组，分别表示成变量t的函数，即给定一个确定的t值，可以求出对应唯一的x和y的值，但x和y不一定具有函数关系.普通方程和参数方程是同一曲线的不同表达形式，它们之间可以互相转化.圆一直以来都是学生学习的难点内容，利用参数方程，可以帮助学生解题更直观化.如下面题目所示：

例1 (2014·辽宁卷)将圆x2+y2=1上每一点的横坐标保持不变，纵坐标变为原来的2倍，得曲线C：

(1)写出C的参数方程；

(2)设直线Z：2x+y-2=0与C的交点为P1，P2，以坐标原点为极点，x轴正半轴为极轴建立极坐标系，求过线段P1P2的中点且与l垂直的直线的极坐标方程．

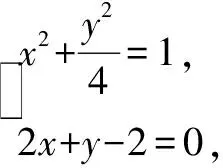
二、椭圆的应用

参数方程在椭圆中也有广泛应用，一般常用于求解函数或者代数式的最值，主要的求解步骤为：一，先写出椭圆的参数方程；二，用椭圆中参数表示成已知的函数或者代数式；三，利用三角函数的公式求出最值.我们还可以利用参数方程求出椭圆的轨迹，主要是利用θ的作用来对坐标进行表示，之后再用sin2θ+cos2θ=1进行消参数即可.如在下列例题中，答案运用了参数方程和普通函数方程的转化以及参数方程求最值，相比于传统的教学方法，更简便.因此，教师在进行教学时要引导学生灵活运用参数方程，培养学生学会数形结合.

(1)若a=-1，求C与l的交点坐标；

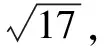
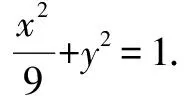
当a=-1时，直线l的普通方程为x+4y-3=0.

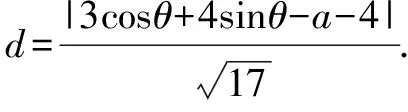
综上，a=8或a=-16.

三、双曲线的应用

高中数学中存在不少与数量有关的难题，特别是在双曲线中，题目一般综合性较强、难度较大，需要学生能通过基础知识发散思维，找到解题的诀窍.参数方程双曲线中也有很广泛的应用，主要是用x和y进行表示，x=a·secθ(正割)，y=b·tanθ，a为双曲线实轴的一半，b为双曲线虚轴的一半，θ为参数，焦点在x轴上.通常情况下，我们使用参数方程求双曲线的与渐近线有关的图形的面积，类似上面的例题，先利用参数方程找出交点坐标，再利用面积公式和正余弦定理求解相比于直接求解，使用参数方程大大简化了求解步骤和时间，对学习解题速度的提高帮助很大.

总的来说，数学是高中教育的重要学科，教师在课堂教学时不能只是讲解例题的解题过程，而是要注重解题技巧的讲解.参数方程在数学中应用广泛，有助于发挥学生创新性的解题思维，解决学生的数学的瓶颈问题.我们教师要帮助学生学会灵活利用参数方程解决问题，进一步提高解题效率，促进高中数学教学质量的稳步提高.

参考文献：

[1]毛芹.圆锥曲线参数方程在高中数学解题中的应用Ⅱ[J].理科考试研究:高中版,2014(21).

[2]陈尧明.直线参数方程教学设计[J].教学月刊:中学,2011(23).

[3]李淑燕.用圆锥曲线的参数方程解题例谈[J].数理化学习:高三,2017(7).

[4]陈传熙.“圆锥曲线的参数方程”的教学困惑与对策分析[J].数学通报,2010(49).