用一简单函数证明均值不等式

储百六

(安徽省岳西中学 246600)

函数f(x)=ax+a-x是我们非常熟悉的函数，其推广后可以得到n元均值不等式的一个漂亮证明.

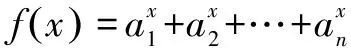
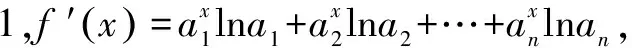
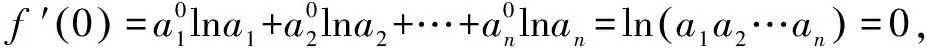
于是，当x<0时，f′(x)0时，f′(x)>f′(0)=0.

所以函数f(x)在(-∞,0]上为减函数，在[0,+∞)上为增函数.

定理1(均值不等式的证明)

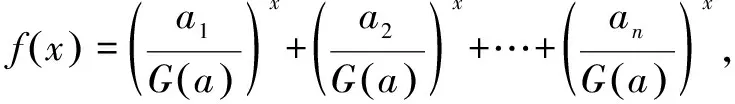
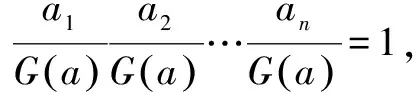
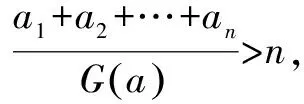
(2)当a1=a2=…=an时，显然A(a)=G(a)=H(a).

综合(1)(2)可知：A(a)≥G(a)≥H(a)，当且仅当a1=a2=…=an时取等号.

说明利用f(x)的单调性易得：f(k)≥f(k-1),k∈N*，整理得：

于是可得不等式链：

定理2(加权均值不等式的证明)

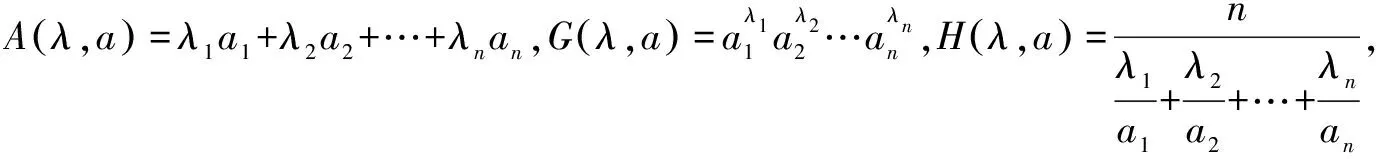
先证明一个引理

所以f′(x)在R上为增函数.

于是，当x<0时，f′(x)0时，f′(x)>f′(0)=0.

所以函数f(x)在(-∞,0]上为减函数，在[0,+∞)上为增函数.

再证明均值不等式.

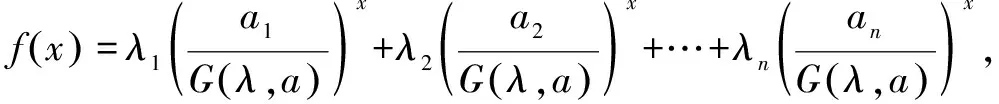
由引理2知函数f(x)在(-∞,0]上为减函数，在[0,+∞)上为增函数.

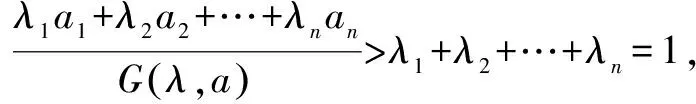
于是A(λ,a)>G(λ,a)；

(2)当a1=a2=…=an时，显然A(λ,a)≥G(λ,a)≥H(λ,a).

综合(1)(2)可知：A(λ,a)≥G(λ,a)≥H(λ,a)，当且仅当a1=a2=…=an时取等号.

参考文献：

[1]常庚哲,史济怀.数学分析教程[M].合肥：中国科学技术大学出版社,2012(8).