对偶思想在中学数学的渗透
2018-06-06杨伟达
杨伟达
(广东省广州市花都区第二中学 510820)
众所周知,数学和古诗词一样讲究对偶.而这种“对偶”常常渗透到中学数学的各个领域,体现了数学的和谐、统一、对称、简洁. 它的美极大地吸引无数数学爱好者,去体验数学的魅力,去感受到数学的乐趣. 因此,在解题教学中有意识渗透这种对偶思想,对培养和发展学生的创造性思维大有帮助.笔者就对偶思想的统一性、和谐性、对称性逐一举例说明,以飨读者.
一、对偶思想的统一性
对偶思想的统一性体现了整个命题的完整性,导出了部分与整体、部分与部分的关系.它渗透到集合与映射、函数、二项式的排列组合、数列的倒序、立体几何的倒放等.
例1 设(1-x+x2)50=a0+a1x+a2x2+…+a99x99+a100x100.求下列间隔为3的系数之和:
M1=a0+a4+a8+…+a96+a100;
M2=a1+a5+a9+…+a93+a97;
M3=a2+a6+a10+…+a94+a98;
M4=a3+a7+a11+…+a95+a99.
分析观察各个系数之和的特点,发现系数很有规律,系数的下标是公差为4的等差数列.其中M1+M2+M3+M4为全部系数之和;M1+M3为偶数系数之和;M2+M4为奇数系数之和.由此可见,求系数之和常常采用赋值法.不妨赋值为1,-1,i,-i即可.
解对上述二项式x的分别为1,-1,i,-i代入得:
a0+a1+a2+a3+…+a99+a100=1 (1)
a0-a1+a2-a3+…-a99+a100=350(2)
a0+a1i-a2-a3i+…-a99i+a100=-1 (3)
a0-a1i-a2+a3i+…+a99i+a100=-1 (4)
根据各系数的特点,联立(1),(2),(3),(4)方程
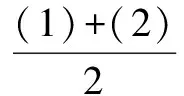
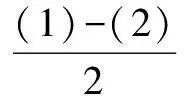
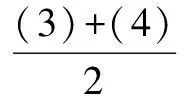
a0-a2+a4+…-a98+a100=-1, (7)
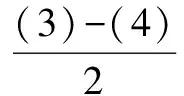
a1-a3+a5+…+a97-a99=0. (8)
再分别将方程(5),(6),(7),(8)联立,
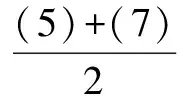
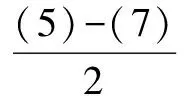
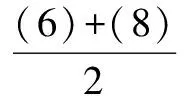
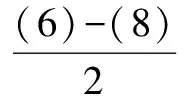
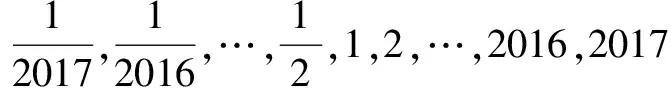
分析在所给数值中发现两两互为倒数,故不妨从倒数变换入手.
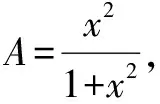
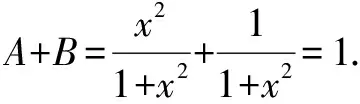
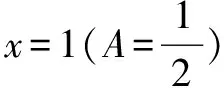
二、对偶思想的和谐性
对偶思想的和谐性:关键在于一个与之对应的有效式子,双双参与运算.体现在函数(如:af(x)+bg(x)=?或af(x)-bg(x)=?)、三角函数、解几、方程、复数的共轭化等.
例3 求x=cos20°cos40°cos80°的值.
分析此题涉及三角化简求值.观察题设的条件是以乘积的形式出现,且角度成2倍关系,不难想象到用二倍角公式处理.因此需要“补形还原”即可.
解除常规的积化和差外,还可以用对偶化,

再利用sin2α=2sinαcosα得:
xy=cos20°cos40°cos80°sin20°sin40°sin80°
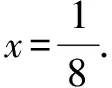
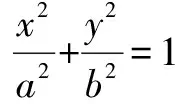
分析此题涉及解析几何的常规题型.因已知出现左右焦点,不难想象用概念定义,通过联立方程组即可求解.
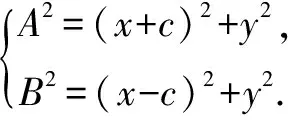
两式相减可得(A+B)(A-B)=4cx,

解得A=a+ex,即|MF1|=a+ex.
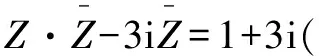
分析一般情况不妨设Z=a+bi,Z=a+bi(a,b∈R),代入后利用复数相等的条件,可求a,b的值.除常规的代入法外,可采用复数共轭化列出方程组,避开了复数的代数式,直接变为复系数的一元二次方程即可求解.
解将复数方程共轭化:
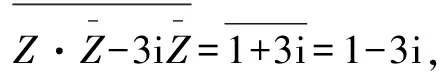
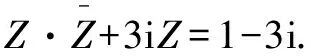
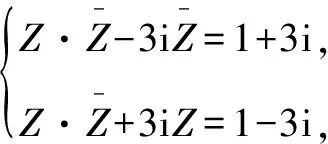
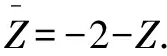
代入原方程可化为一元二次方程,即
Z2+(2-3i)Z+(1-3i)=0.
Δ=(2-3i)2-4×1×(1-3i)=-9,
所以原方程的解为
三、对偶思想的对称性
对偶思想的对称性表现在命题本身具有对称性,从而使命题简单化.如函数、立几、解几等.形如圆、球,长(正)方形、长(正)方体等图形都可以通过它们的中心找到其特性(对称性),从而快速、巧妙地解决了与之相关的数学问题.
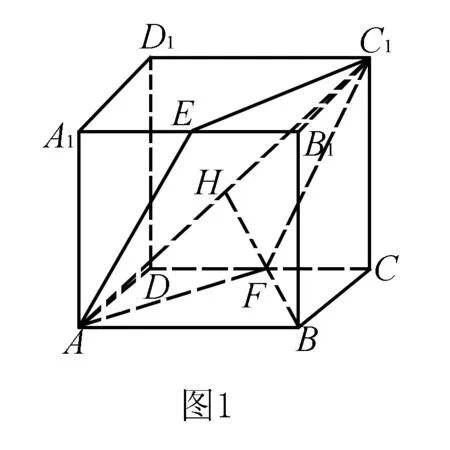
例6 如图1,在正方体ABCD-A1B1C1D1中,E,F分别是A1B1、CD的中点,求直线AB与平面AEC1F所成角的正切值.
分析按常规思路,学生总是通过B点作平面AEC1F的垂线BH,H为垂足,然后再证明在正方体的对角线AC1上.我们若注意到正方体中诸多的对称性,就不难发现面ABB1E与面ABCF是关于面ABC1D1对称的,E、F是关于AC1对称的,从而B在面AEC1F内的射影H必须在AC1上,故找到直线AB与平面AEC1F所成角为∠BAC1.
在Rt△BAC1中即可求得∠BAC1的正切值.
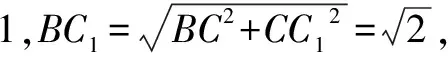
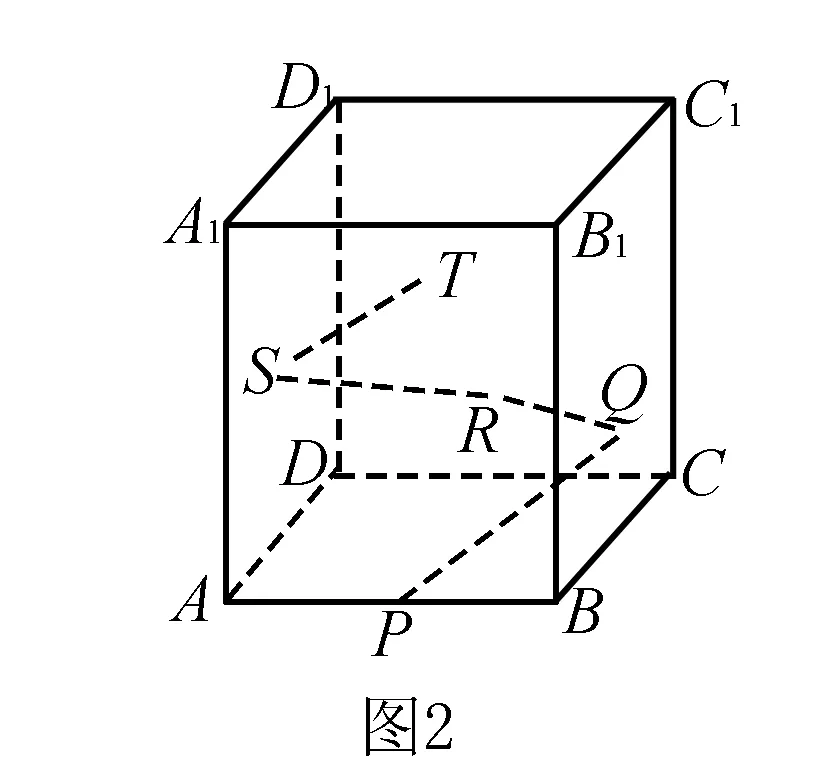
例7 如图2,在正方体ABCD-A1B1C1D1中,棱AB的中点为P,若光线从点P出发,依次经三个侧面BCC1B1,DCC1D1,ADD1A1反射后,落到侧面ABB1A1内(不包括边界),则入射光线PQ与侧面BCC1B1所成角的正切值的范围是____.
分析本题涉及光线镜面反射问题.解决此问题其实是数学上的对称问题.可以先从直线的反射说起,然后把面对称过去,最后成了一条直线.不妨通过补形转化为求两点间的距离最小,再利用极限思想即可将问题解决.
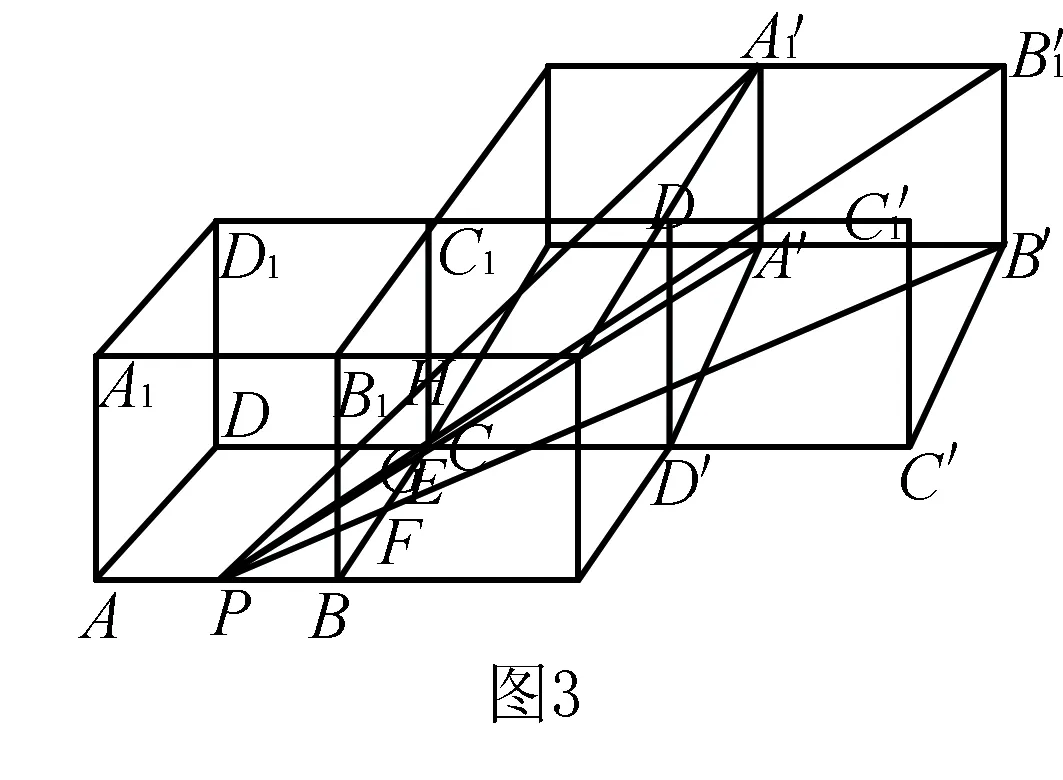
在解题教学中,笔者认为能够有意识地提及对偶思想,对激发学生的思维,选用合理简捷的解法,可以节省时间和精力,还可以化难为易,化繁为简,对提高学生的兴趣,培养和发展的创造性思维,从而实现素质教育.
参考文献:
[1]李成友.感悟对偶思想拓展教学空间[J].数学通讯,2012(05).
[2]韩毅.对偶思想在解题中的应用[J].数学教学通讯,1993(03).
