应用SAPSO-BP神经网络的DOA估计方法
2018-06-06姚建丽胡红萍白艳萍王建中
姚建丽,胡红萍,白艳萍,王建中
(中北大学 理学院, 太原 030051)
在20世纪50年代,矢量水听器的研制就已经出现在美国。它的出现及时地弥补了声压水听器的缺陷,即不能完整地接受声场的信息[1]。自此,很多研究人员对矢量水听器进行了研究。其中,矢量水听器的阵列处理方法和波达方向角是人们研究的重点及热点[2]。
通常解决DOA估计的方法有两种。第1种方法是传统的方法,利用纯数学模型,但要进行大量的运算才能得到最终的结果,比较典型的是1975年Schmidt[3]提出的多重信号分类(multiple signal classification,MUSIC)算法以及Roy等[4]提出的旋转不变子空间(estimating signal parameters via rotational Invariance techniques,ESPRIT)算法。在此基础上,这些算法又衍生出一系列新的算法,如在MUSIC算法的基础上出现了解求根MUSIC算法[5]、波束空间求根 MUSIC算法[6]等。在ESPIT算法的基础上也出现了一些算法,比较有代表性的包括LS-ESPRIT算法[7]、TLS-ESPRIT算法[8]等。另一种是利用智能学习、“软建模”的方式进行DOA估计,其中的重要方法是采用神经网络。张旻等[9]选取协方差矩阵的上三角特征作为网络的输入,采用RBF神经网络来进行DOA估计。孟非等[10]同样选取协方差矩阵的上三角特征作为输入,运用PSO-BP算法对DOA进行估计。赵晓萌等[11]针对BP神经网络的缺陷,运用模拟退火算法对BP神经网络进行优化,提升其效果。
本文对阵列信号的协方差矩阵依次进行实值化和特征分解,选取信号子空间的基作为网络的输入,利用提出的模拟退火粒子群算法优化BP神经网络,实现DOA估计。
1 阵列信号模型
收集信号数据时通常情况下需要用比较规律的天线阵元来进行,本文以均匀等间距线阵为例进行讨论,如图1所示。

图1 DOA估计的一般模型(均匀线性)
考虑N个远场窄带信号以{θ1,θ2,…,θN}的角度入射到M元阵列,阵列的接受信号为
Z(t)=A(t)S(t)+N(t)
(1)
其中:Z(t)是阵列输出矢量;S(t)信号源矢量;N(t)是高斯白噪声矢量,信号与噪声是相互独立的;A(θ)是矢量水听器的方向矢量矩阵。
A(θ)=[a(θ1),a(θ2),…,a(θN)]=
[a(θ1)⊗u1,a(θ2)⊗u2,…,a(θN)⊗uN]
(2)

R=E[Z(t)Z(t)H]=
AE[S(t)S(t)H]AH+E[N(t)N(t)H]=
ARsAH+σ2I
(3)
其中:Rs是入射信号的协方差矩阵;σ2是阵列接收信号中噪声的功率;I是归一化下噪声的相关矩阵;(·)H代表复共轭转置。
根据子空间分解理论,特征分解为
(4)
其中有特征值为λ1≥λ2≥…≥λN≥…≥λ3M,∑s=diag(λ1,λ2,…,λN),∑n=diag(λN+1,λN+2,…,λ3M)。Us是信号子空间,它是由前大N个特征值对应矢量张成的子空间,有Us=[e1,e2,…,en],e1,e2,…,en是它的特征向量。UN是噪声子空间,它是由 3M-N个特征值对应矢量张成的子空间,UN=[eN+1,eN+2,…,e3M],eN+1,eN+2,…,e3M是它的特征向量。

(5)
2 模拟退火粒子群算法优化BP神经网络
2.1 粒子群算法
粒子群(particle swarm optimization,PSO)算法是Eberhart和Kennedy在1995年根据对鸟类捕食行为的研究提出的一种群优化算法[12]。在PSO算法中,每个粒子被看作是一个潜在解,每个粒子对应适应度函数的适应度值,粒子的速度决定粒子本身的运动方向和距离,粒子的速度根据自身及其他粒子的运动情况可以进行动态调节,从而可以得到最优解。
在每一次迭代过程中,粒子更新自身的速度和位置的核心公式如下:

(6)
(7)

本文中所使用的惯性权重公式为:
(8)
式中:max gen为最大的迭代次数;wstart和wend分别为初始的惯性权重和最大迭代数时的惯性权重。本文中wstrat=0.95,wend=0.4。
2.2 模拟退火算法
SA算法最开始是在1953年由N.Metropolis等提出的。1983年,S.kirkpatrick等将SA思想成功地引入组合优化领域[13]。SA是一种随机寻优算法,是基于Monte-Carlo迭代方法求解形式进行的,它以物理固体物质的退火过程与一般组合优化问题之间的相似性为出发点。SA算法由于独特的概率突跳能力,在全局搜索极值中起到了很大的作用,并被应用于很多方面。
用热力学系统来进行解释,SA算法的基本思想是把系统的能量看成目标函数,把系统逐步降温达到最低能量状态的过程看作优化过程。SA算法设定一个较高的温度,从这一个温度开始,随着温度的不断下降,结合概率突跳的特点在解空间范围内寻找全局最优解。也就是说,当目标函数得到局部最优解时,可以一定的概率跳出局部最优并最终趋于全局最优解。SA 算法在搜索过程中具有一定概率的突跳能力,能有效地避免在搜索过程陷入局部最优解。
2.3 模拟退火粒子群算法
PSO算法所需的参数少,操作较为简单,具有很强的适用性。在算法初期时收敛速度快,但在后期容易受到随机振荡的影响,从而导致收敛速度降低,陷入局部最小值。本文借鉴模拟退火算法中的概率突跳能力,使粒子以一定的概率跳出已搜索的最优区域在更大空间中开展搜索,提出了模拟退火例子群算法,记为SAPSO算法,具体步骤如下:
1) 对粒子的速度和位置进行初始化,对退火速度进行初始化。
2) 种群中每个粒子根据适应度函数计算其适应度值。
3) 比较粒子新位置的适应度值与之前找到的最佳适应度值的大小,如果新位置的适应度值更佳,则更新当前位置为最佳位置。
4) 将所有粒子的历史最优适应度值与群体经历过的最佳位置进行比较,如果目前的位置最佳,则用当前位置取代原来位置作为全局最佳位置。
5) 更新粒子的位置和速度。
6) 判断是否达到终止条件,若是则将权、阈值赋予BP网络的初始权值w和阈值B;否则,返回步骤3)继续。
7) 引入模拟退火算法继续训练寻优,令wi′ =wi+Δwi,Bi′ =Bi+ΔBi,Δw、ΔB均为很小的均匀分布的随机扰动。目标函数为
(9)
式中:N是训练样本总数;y(k)是期望输出;d(k)是实际输出。得到两个位置的适应度值变化量为ΔE=E(pi′)-E(pi)。
8) 如果ΔE<0,则把w′,B′作为新的权值和阈值,否则以概率为P=exp(-ΔE/Ti)接受w′、B′为新的当前解,并更新参数。
9) 重复步骤7)和8),直到系统得到平衡状态。
10) 进行降温,T逐渐减少,退火机制为
Tk=aT0
(10)
其中:a表示退火速度;T0为初始温度。
11) 重复步骤7)~9),直到T=0或者达到预设温度。
12) 网络训练结束,得到的最新权值和阈值为BP神经网络的权、阈值。
2.4 SAPSO优化BP神经网络
BP(back propagation)神经网络由Rumelhart和McCelland为首的科研人员在1986年提出,它是一种多层反馈网络,是目前应用最为广泛的神经网络模型之一[14-19]。BP神经网络由输入层、隐层和输出层3部分网络结构构成。它的学习规则是梯度下降法,通过信号的正向传播以及误差的反向传播不断调整网络的权、阈值,最终实现误差的平方和最小。
本文采用SAPSO算法得到的最优解作为BP神经网络的初始权、阈值,选取信号子空间的基作为BP神经网络的输入,经过BP神经网络训练其权、阈值,建立DOA估计预测模型,流程如图2所示。
3 仿真实验
3.1 实验1: 两信号源的来波方向估计
实验的天线阵列为均匀的5元线阵,信号源选用两个正弦信号,信噪比为10 dB,快拍数为1 000,进行200次Monte-Carlo仿真实验。

图2 基于信号子空间的SAPSO-BP算法流程
训练数据:信号源之间的间隔分别取12和18,当间隔取12时,从-90到65每隔0.5取1个样本,得到样本数311个。如果用向量X1、X2分别表示两个信号的角度,则X1=[-90,-89.5,-89,…,64.5,65]T,X2=[-78,-77.5,-77,…,76.5,77]T。通常采用的是二维矢量水听器,可输出声压p(t)、振速vx(t)、vy(t)3路信号,本文采用5元线阵,会产生15路信号。同样地,当间隔取18时,从-90到65每隔0.5取1个样本,得到样本数311个,两个信号的角度为:X1=[-90,-89.5,-89,…,64.5,65]T,X2=[-78,-77.5,-77,…,82.5,83]T,同样会产生15路信号。训练数据的总样本为622。
测试数据:从-90到65每隔1取一个样本,得到测试样本156个。
本文分别利用BP神经网络、PSO-BP网络、SAPSO-BP网络对两信号源的DOA方向进行估计,得到双信号的DOA估计和估计误差,分别如图3~6所示。

图3 第1个信号的DOA估计输出曲线
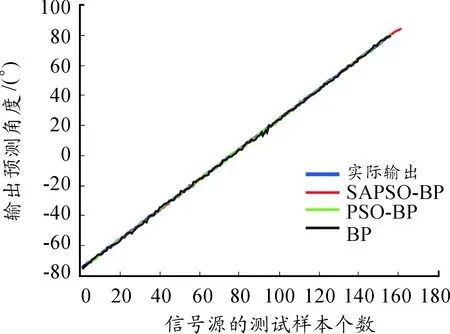
图4 第2个信号的DOA估计输出曲线

图5 第1个信号的DOA估计误差曲线

图6 第2个信号的DOA估计误差曲线
图3是第1个信号在3种模型下的DOA估计值和实际值,图4是第2个信号在3种模型下的DOA估计值和实际值。通过图3、4可以看出:在SAPSO-BP情况下的预测值更接近实际值,而BP神经网络的预测值与实际值的差距最大,PSO-BP网络的预测值与实际值情况居中。图5是第1个信号在3种模型下的DOA估计的误差曲线,图6是第2个信号在3种模型下的DOA估计的误差曲线。从图5、6可以看出:使用SAPSO-BP网络估计DOA的误差最小,而BP神经网络估计DOA得到的误差最大。通过DOA输出曲线和误差曲线可以看出,本文提出SAPSO-BP方法用于DOA估计有更高的精度。
表1是3种模型下的MAE、MSE、RMSE值。在不同的模型中,左侧一列为第1个信源的各个指标,右侧为第2个信源的指标。从数据中可以看出:SAPSO-BP的MAE、MSE、RMSE都是最小的,BP的各项指标是最大的,可以得到采用SAPSO-BP对DOA进行估计有一定的优势。
3.2 实验2: 不同信噪比下的性能分析
仿真条件与实验1情况相同,依次估计在信噪比-10、-5、0、5、10、15 dB之间的均方根误差。表2为3种算法在不同的信噪比下的均方根误差。均方根误差的公式为
(11)

表2中选取的值为两个信号源均方根误差的均值,从表2可以看出:随着信噪比的不断增加,信源的均方根误差在不断减小。PSO-BP和SAPSO-BP网络的均方根误差要比BP网络好的多,对比PSO-BP和SAPSO-BP,SAPSO-BP整体来说要比PSO-BP的均方根误差低。因此,本文提出的SAPSO-BP方法有较好的估计精度。
4 结束语
本文针对PSO算法后期容易受到随机振荡的影响而导致收敛速度降低的问题,借鉴模拟退火算法中的概率突跳能力,提出了模拟退火粒子群算法(SAPSO算法)优化BP神经网络(SAPSO-BP),实现双信号的DOA估计和在不同信噪比下的误差估计。将矢量水听器阵列的信号处理模型的协方差矩阵进行实值化并特征分解,选取信号子空间的基作为BP神经网络、PSO-BP网络和SAPSO-BP网络的输入。通过比较,本文提出的SAPSO-PSO网络优于BP神经网络和PSO-BP网络,具有更好的估计精度。但由于BP神经网络自身的局限性,对于DOA估计仍有一定的不足,需要进一步改善。
[1] 王鹏.基于MEMS矢量水听器阵列的声目标定向定位技术研究[D].太原:中北大学,2013.
[2] LI B,PENG C Y,BISWAS S.Association of DOA Estimation from Two ULAs[J].IEEE Transactions n Instrumentation and Measurement,2008,57(6):1094-1101.
[3] SCHMIDT R O.Multiple emitter location and signal parameter estimation[J].IEEE Transactions on Antennas and Propagation,1986,34(3):276-280.
[4] ROY R,PAULRAJ A,KAILATH T.Estimation of signal parameters via rotational invariance techniques-ESPRIT[C]//California:Conference on C ircuits,Systems and Computers.1985:83-89.
[5] RAO B D,HARI K.Performance analysis of root-MUSIC[J].IEEE Transactions on Acoustics,Speech and Signal Processing,1989,37(12):1939-1949.
[6] ZOLTOWSKI M D,KAUTZ G M,SILVERSTEIN S D.Beamspace root-MUSIC[J].IEEE Transactions on Signal Processing,1993,41(1):344-364.
[7] ROY R,PAULRAJ A,KAILATH T.ESPRIT—A subspace rotation approach to estimation of parameters of cisoids in noise[J].IEEE Transactions on Acoustics,Speech,and Signal Processing,1986,34(5):1340-1342.
[8] ROY R,KAILATH T.ESPRIT-estimation of signal parameters via rotational invariance techniques[J].IEEE Transactions on Acoustics,Speech and Signal Processing,1989,37(7):984-995.
[9] 张旻,李鹏飞.基于分层神经网络的宽频段DOA估计方法[J].电子与信息学报,2009,31(9):2118-2122.
[10] 孟非.基于PSO-BP神经网络的DOA估计方法[J].电讯技术,2012,52(5):694-698.
[11] 赵晓萌,刘李楠.基于模拟退火方法BP神经网络的测向定位方法[J].安阳工学院学报,2012,11(2):35-38.
[12] 潘昊,候清兰.基于粒子群优化算法BP网络学习研究[J].计算机工程与应用,2016(16):41-42.
[13] KIRKPATRCK S,GELATT C D,VECCHI M P.0ptimization by simulated amealing[J].Science,1983(220):67l-680.
[14] 齐浩淳,黄大鹏,魏久南,等.基于BP神经网络的高寒山地弹药消耗需求分析[J].兵器装备工程学报,2016,37(6):97-101.
[15] 王永杰,白艳萍.基于主成分分析的PSO-BP算法在GDP和CPI预测中的应用[J].重庆理工大学学报(自然科学),2017,31(4):150-154.
[16] 李红连.BP神经网络在车辆组合导航中的应用研究[J].压电与声光,2011,33(1):45-48.
[17] 张虹,王丹.一种改进的BP神经网络剪枝算法研究[J].西南大学学报(自然科学版),2016,38(3):165-170.
[18] 刘彩红.一种优化BP神经网络训练样本的方法[J].重庆师范大学学报(自然科学版),2007,24(3):51-53.
[19] 高隽.人工神经网络原理及仿真实例[M].2版.北京:机械工业出版社,2007:10-11.
