低碳排放约束下城市停车换乘设施规划研究
2018-06-06邓红星李嘉璐
邓红星,李嘉璐
(东北林业大学 交通学院, 哈尔滨 150040)
随着机动车数量的急剧增长,城市中交通拥挤和交通排放污染问题日益加剧。许多研究将排放收费或拥挤收费作为研究对象,虽然这样可以缓解交通拥堵,减少交通排放,但随着城市规模的不断扩张,依靠收费策略限制出行的效果有限,因此停车换乘被认为是缓解城市交通压力的有效手段之一[1]。在研究减少交通排放方面, Sharma和Mishra[2]提出了最优排放定价模型,使得在综合运输网络中温室气体排放降低到一定比例,模型同时考虑政策决策者和出行者,具有一定的适用性。张鑫等[3]提出了既能降低用户出行时间又能满足低碳约束条件的排放收费模型。在研究微观交通排放问题时,一般考虑机动车工况运行情况对排放的影响。刘畅[4]利用双层规划理论,将交叉口的信号配时和排放收费有机结合,从中观角度建立交通排放控制模型,对配时方案和收费费率进行优化。在研究停车换乘收费策略问题时,赵顺晶等[5]提出用一个双层规划模型来描述停车换乘条件下换乘停车费用的优化问题,其以系统总阻抗最小为目标,研究不同换乘停车费用设置方案下出行者基于随机用户平衡的路径选择行为。Faghri等[6]提出了一种帮助规划者确定停车换乘最优位置的系统。该系统提出用多个指标考察备选解,如靠近CBD、靠近地铁站等。刘颖[7]建立了基于社会最优的停车换乘系统定价模型,指出拥挤收费与停车换乘收费存在竞争关系,并通过模型求解费率证明模型的科学性与有效性。本文在停车换乘模式下研究满足宏观低碳环境排放要求的停车换乘设施规划问题,建立同时考虑停车设施运营者和出行者的双层规划模型。
1 停车换乘出行路网描述
为描述出行者在停车换乘出行过程中客流分配情况,基于小汽车、地铁、常规公交3种出行方式构建分层交通网络,从出行时间、出行时间可靠性、货币费用3方面定义广义出行费用。假定在路网需求为弹性的情况下,出行者以估计的广义出行费用最小为路径选择的标准,应用Logit概率选择模型进行客流分配。
1.1 分层交通路网的描述
定义一个有向的交通网络G=(N,L),其中N为节点集,L为路段集。O为起始节点集,O⊂N;D为终讫节点集,D⊂N;r为起始节点,r∈O;s为终讫节点,s∈D。A为行驶路段集合,E为换乘路段集合,L=A∪E,l为其中的一条路段。I为交通方式集合,i为一种交通方式,i=1,2,3分别代表小汽车、地铁和常规公交,Ni和Li分别为各子网的节点集和路段集。因此,研究的出行交通路网的集合为G1=(N1,L1),G2=(N2,L2),G3=(N3,L3),各子网之间通过换乘路段连接。由此可将普通路网转化为分层级路网,如图1所示。

图1 普通路网转为分层级路网
假设停车换乘模式满足要求:① 各种出行方式互不干扰,独立成网;② 只考虑单一用户类型情况,所有出行者对时间价值判断标准一致;③ 公共交通层级网络优于小汽车交通网络。考虑以下几种情况:小汽车的出行直达,小汽车换乘地铁的出行,小汽车换乘常规公交的出行。
1.2 停车换乘模式下需求函数和费用函数

1.2.1 需求函数
在SUE模型中,任意OD对之间的出行需求可以表示为期望最小出行成本的单调下降函数,即
qw=Dw(Sw),w∈W
(1)
式中Sw为OD对w间的最小期望出行费用,有
(2)

(3)
式中θ2为模型的校正参数,反映出行者对出行路径p的感知费用误差程度。根据树形结构行为选择理论的要求[9],θ2≥θ1>0。
1.2.2 停车换乘的费用函数
路网中的广义路径费用可表示为各路段费用之和,即
(4)

分层交通网络路段包括行驶路段和换乘路段。将小汽车的经济费用、公交与地铁的票价转到换乘路段费用上。路段的广义费用由出行时间、货币费用、出行时间可靠性3种因素构成,则路段费用为
(5)

1) 行驶路段费用
① 小汽车
小汽车行驶路段的出行时间可由BRP函数给出。货币费用通过路段长度与单位长度的燃油费计算得到。小汽车路段行程时间可靠性定义为路段行程时间不大于可接受阈值的概率,阈值一般是路段自由行程时间的函数,可取固定值。文献[14]对交通流历史数据所做的实证分析认为路段出行时间在较长时期内可近似看作服从均值为tl和标准差为σl的正态分布,具体表达式如下:
(6)
(7)
(8)

② 地铁
地铁出行的时间由地铁运行时刻表决定,具体表达式如下:
(9)
(10)
(11)

③ 常规公交车
公交车出行时间由公交时刻表决定。将公交在路段的运行时间可靠性定义为车辆在起点站和到达站之间运行时间在给定的阈值范围内的概率[11],表示为:
(12)
(13)
(14)

2) 换乘路段费用
换乘路段费用的出行时间包括步行时间与等待时间;换乘路段上的费用为换乘时所支付的公共交通的票价和小汽车停车换乘的经济费用。在换乘过程中,可能因拥挤状况导致无法上车的情况增加了等待时间,产生了不可靠性。具体表达式如下:
(15)
(16)
(17)

2 双层规划模型
通过停车换乘设施的规划,影响小汽车及公交车出行比例,同时满足低碳环境约束目标,起到缓解交通拥挤及鼓励出行者选择公共交通出行的目的。建立同时考虑停车设施运营者和出行者的双层规划模型。
2.1 上层模型
上层模型从停车设施运营者角度出发,以低碳排放环境为约束,运营收益最大为目标。本文忽略地铁的碳排放量。根据文献[12]采用适用于宏观的CO2排放因子计算模型,宏观CO2排放因子是由权威部门发布的平均统计意义上的排放因子,不考虑运行工况影响,适用于分析统计某一区域不同客运交通方式的排放量。表达式如下:
(18)
其中:Fbase为不采取干预措施下交通网络的碳排放量;la和lb为路段长度;xa和xb为不同出行方式路段流量;RF1和RF2为小汽车与常规公交的CO2排放因子。
Fmax=Fbase×(1-α)=
(19)
其中:α为预期减排目标,由规划者或政策制定者根据交通区域特性确定;Fmax为交通网络碳排放量的上限。
运营收益Z=总收入-(运营成本+投资成本),具体表达式如下:
(20)
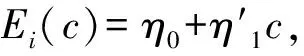
2.2 下层模型
2.2.1 随机用户平衡条件
多方式交通网络达到随机平衡状态即没有出行者能通过单方面改变出行路径来减少最小期望出行费用,满足Logit随机平衡,具体表达式如下:
m∈M,w∈W
(21)
p∈Pw,m∈M,w∈W
(22)
2.2.2 模型的建立
根据上述平衡条件,构造变分不等式:
(23)

3 模型的求解算法
在双层规划问题中,群优算法因具有搜索能力强、可并行计算等优点被广泛应用。本文根据模型特点设计了MSA与遗传算法相结合的求解算法,上层应用遗传算法求出的传递变量(zi,ci)代入下层,利用MSA算法进行交通分配。具体步骤如下:
1) 设置遗传算法相应参数,在约束条件下确定上下限,确定交叉概率Pm、变异概率Pc、初始种群规模和最大迭代次数。
2) 将上层的优化变量(zi,ci)代入下层,利用MSA算法求解下层停车换乘交通网络分配模型。
3) 将下层求解得到的路段流量代入上层,计算上层适应度函数。将满足约束条件的解代入得出适应度函数值;不满足约束的解加1个惩罚因子。
4) 进行遗传操作。根据上述算子进行选择、交叉、变异产生子代。
5) 当达到最大迭代次数,算法终止;否则,返回步骤2)循环继续。
下层MSA算法步骤如下:

4 算例分析
4.1 算例网络


表1 小汽车行驶路段属性

表3 公交运行路段属性
4.2 模型优化结果
1) 根据求解算法得到满足约束的解为最佳收费策略和停车容量,在此停车换乘模式下,可得到上层运营效益Zmax=11 159元。各路段小汽车流量、公交线路1、公交线路2及地铁流量如表4~8所示。

表4 停车收费策略及停车容量
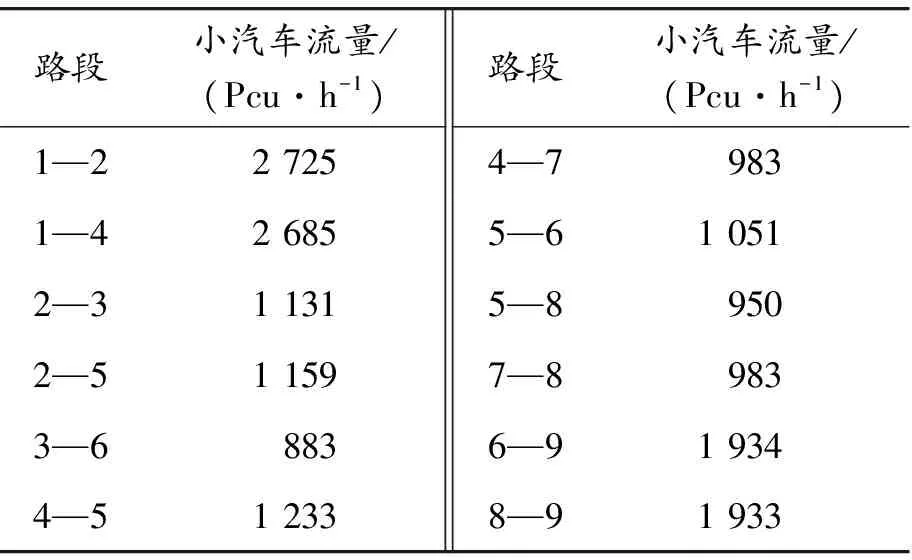
表5 停车换乘模式下各路段小汽车流量

表6 停车换乘模式下各路段公交线路1客流量

表7 停车换乘模式下各路段公交线路2客流量

表8 停车换乘模式下各路段地铁客流量
2) 由下层交通分配结果可以得到各停车换乘站点在出行中所占流量比例,如表9所示。

表9 各换乘站点停车量及分担率
通过各路段流量及站点流量计算可知:在站点2处,65.7%出行者选择停车换乘公交线路1,34.2%的出行者选择停车换乘公交线路2;在站点3处,有21.9%的出行者选择停车换乘公交1线路;在站点4处,有17.5%出行者选择换乘地铁;在站点5处,有6.5%出行者选择换乘地铁,同时1.8%出行者换乘公交线路2。由上述数据可知:当出行距离较远时,出行者倾向于停车换乘出行方式,因此站点2、3、4处换乘比例较高;当距离目的地较近时,人们更倾向于小汽车直达。因此,可以根据距离的不同规划不同的容量及收费策略。当出行者在同一地点换乘时,更倾向于选择地铁出行。
3)经过计算,在本收费策略下,采取停车换乘模式后人均CO2排放量为4.23 kg,较减排目标值4.25 kg低,达到了减排15.4%的效果。
5 结束语
本文研究了满足一定低碳排放指标约束下停车换乘设施规划问题,建立了双层规划模型。上层为考虑停车换乘运营者效益最大的优化模型,下层为基于3种出行方式的停车换乘交通出行网络弹性需求条件下用户均衡分配模型。设计了MSA算法结合遗传算法进行求解。算例结果表明:通过规划设定停车换乘设施的容量及定价策略可以达到控制交通排放的目的。针对算例,采取停车换乘模式后人均CO2排放量为4.23 kg,达到了减排15.4%的效果,并超出目标0.4%,上层运营效益函数达到最大Zmax=11 159元。对于下层,换乘车站与目的地之间距离程度相近时,出行者换乘常规公交的概率高于地铁。例如,在站点2处,65.7%出行者选择换乘公交1,34.2%的出行者选择换乘公交2;在站点4处,有17.5%出行者选择换乘地铁。这是因为地铁换乘过程中换乘费用高于常规公交,规律与实际相符。因此,在设置停车换乘站点时,可以集中规划常规公交线路,以提高公共交通分担率。该模型可以满足低碳条件下运营效益最大的要求,同时也能在一定程度上反映在出行过程中路径选择行为。本文所提出的模型可以为公交票价、停车费用的定制等提供一些思路,具有一定的实际意义。在以后的研究中,可以针对城市交通排放控制区域不同距离条件下停车换乘设施的规划问题进行深入研究。
[1] LAM W H K,HOLYOAK N M,LO H P.How park-and-ride schemes can be successful in Eastern Asia[J].Journal of Urban Planning & Development,2001,127(2):63-78.
[2] SUSHANT S,SABYASACHEE M.Intelligent transportation systems-enabled optimal emission pricing models for reducing carbon footprints in a bimodal network[J].Journal of Intelligent Transportation Systems,2013,17(1):54-64.
[3] 张鑫,刘攀.低碳排放约束下多方式网络最优排放收费研究[C]//第八届中国智能交通年会.合肥:[出版社不详],2013.
[4] 刘畅.考虑环境效益的交通管控策略优化[D].杭州:浙江大学,2017.
[5] 赵顺晶,龙建成.通勤廊道换乘停车费用优化模型及算法[J].系统工程理论与实践,2016,36(9):2337-2344.
[6] FAGHRI A,LANG A,HAMAD K,et al.An integrated knowledge-based geographic information system for determining optimal location of park-and-ride facilities[J].Journal of Urban Planning & Development,2002,128(1):18-41.
[7] 刘颖.拥挤收费背景下换乘停车场的定价理论研究[D].重庆:重庆交通大学,2014.
[8] 孟梦,邵春福,曾静靖.组合出行模式下多方式交通流分配模型及算法[J].吉林大学学报(工学版),2014,44(1):47-53.
[9] 黄海军,李志纯.组合出行方式下的混合均衡分配模型及求解算法[J].系统科学与数学,2006,26(3):352-361.
[10] 陈琨,于雷.基于对数正态和分布的路径行程时间可靠性模型[J].北京交通大学学报,2009,33(3):35-39.
[11] 宋晓梅,于雷.常规公交微观区间运行时间可靠性评价模型研究[J].交通运输系统工程与信息,2012,12(2):144-149.
[12] 张鑫.低碳排放约束下交通网络均衡分析及优化[D].南京:东南大学,2014.
[13] 孟梦.组合出行模式下城市交通流分配模型与算法[D].北京:北京交通大学,2013.
