简单事件概率的求解策略

王晓华

概率是初中数学的主要内容之一.对于本章“认识概率”，同学们需要理解“不可能事件、随机事件、必然事件”三种事件；感受随机事件发生的可能性有大有小；会用频率的稳定值估计概率.下面就和大家聊聊求简单事件发生的可能性（即概率）的策略.

一、判断事件，比较概率

我们都知道，必然事件发生的概率为1；不可能事件发生的概率为0；随机事件发生的可能性有大有小.

【例1】事件A：打开电视，它正在播广告；事件B：抛掷一个均匀的骰子，朝上的点数小于7；事件C：在标准大气压下，温度低于0℃时冰融化.三个事件的概率分别记为P（A）、P（B）、P（C），则它们的大小关系正确的是（ ）.

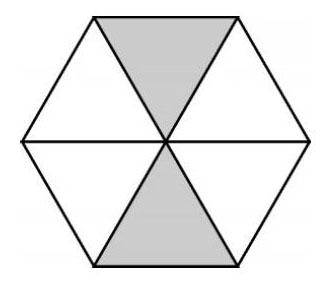
A.P（C）

C.P（C）

【策略】本题考查了几种事件及其对应的概率.必然事件概率是1.不可能事件概率为0.不确定事件就是随机事件，发生的概率是0和1之间的一个数.解决此类问题，我们要判断出事件的类型，然后根据不可能事件、随机事件、必然事件的概率排序即可.

【解】事件A是随机事件，0

二、一一列举，简单计算

列举法是概率运算中最简单实用的方法，它适用于一些涉及一步试验的简单事件.根据随机事件概率大小的求法，找准两点：①符合条件的情况数目；②全部情况的总数.二者的比值就是某一个随机事件发生的概率的大小.

【例2】掷一枚均匀的标有1、2、3、4、5、6的骰子，有下列几种可能发生的事件：①掷得的数是奇数；②掷得的数是3的倍数；③掷得的数大于1.按每个事件发生的可能性的大小从小到大的顺序排列：___________（只填序号）.

【策略】可能性大小的比较：只要总情况数目相同，谁包含的情况数目多，谁的可能性就大.反之也成立.若各事件包含的情况相当，那么它们的可能性就相等.

【解】掷一枚骰子，可能会出现1、2、3、4、5、6共六种可能的结果.①掷得的数是奇数的结果可能是1、3、5，共三种情况，概率为[3/6]=[1/2]；②掷得的数是3的倍数的结果可能是3、6，共两种情况，概率为[2/6]=[1/3]；③掷得的数大于1的结果可能是2、3、4、5、6，共五种情况，概率为[5/6].故答案为②①③.

三、几何助阵，方便求解

“数”和“形”之间有着密切的联系，在一定条件下，可以相互转化，相互渗透.当每个事件发生的可能性只与构成该事件区域的长度、面积或体积等成比例时，我们可以从几何的角度来求解.利用几何的方法探求概率的过程，体现了“数形结合”的思想方法.

【例3】如图所示的六边形广场由若干个大小完全相同的黑色和白色正三角形组成.一只小鸟在广场上随机停留，刚好落在黑色三角形区域的概率为P1，落在白色三角形区域的概率为P2 .则P1_____P2（填“>”“=”或 “<”）.

【策略】本题可以借助图形面积获解，体现了“数形结合”的思想.只要弄清黑色区域面积和整个图形面积的关系、白色区域面积和整个图形面积的关系即可.

【解】根据题意，这个六边形广场是由六个完全相同的三角形组成.黑色区域的面积是整个图形面积的[2/6]=[1/3].所以，小鸟刚好落在黑色区域的可能性为[1/3].白色区域的面积是整个图形面积的[4/6]=[2/3].小鸟落在白色区域的可能性为[2/3]. 故P1

四、另辟蹊径，巧算概率

对于某些事件，采用列举法求概率可能会比较烦琐.此时不妨另辟蹊径，换个角度思考.

【例4】小明与父母从北京乘火车回无锡，他们买到的火车票是同一排相邻的三个座位.小明恰好坐在父母中间的概率是 .

【策略】常规思路：先利用列举法写出所有等可能的结果，再找出“小明坐在中间”这一个事件的结果数，然后求出概率.此处，我们也可以直接思考小明的位置.他可以坐在左边的位置，也可以坐在中间的位置，还可以坐在右边的位置.共三种情况，坐在中间的位置是其中的一种情况.即恰好坐在中间的概率是[1/3].或者从中间位置的角度思考.中间位置可以给爸爸坐，也可以给妈妈坐，还可以给小明坐.共有3种结果.符合条件的有一种，概率是[1/3].

【解】小明恰好坐在中间的概率是[1/3].

五、根据频率，估算概率

在实际生活中，有时我们不能直接通过理论计算求得概率，在很多情况下要进行相应的试验，通过试验、观察、记录、分析，计算出相应的频率来估计概率.

【例5】从某玉米种子中抽取6批，在同一条件下进行发芽试验，有关数据如下：

根據以上数据，可以估计该玉米种子发芽的概率为_________（精确到0.1）.

【策略】此题主要考查利用频率来估计概率.根据频率与概率的关系求解是解答本题的关键，体现了“用频率估计概率”的思想方法.频率是通过试验得到的，它随着试验次数的变化而变化，但当试验的重复次数充分大时，频率会在概率附近摆动.对于本题，要求出种子发芽的概率，我们一般常把试验次数很大时事件发生的频率作为概率的近似值.

【解】该玉米种子发芽的概率为0.8 .

（作者单位：江苏省无锡市新安中学）