无刷直流电机控制系统的研究

(福州大学电气工程自动化学院，福建 福州 350108)

1 引言

无刷直流电机(BLDCM)在某种程度上是同步电机中的一类，简而言之定子旋转磁场的速度和转子极数影响转子的转速。无刷直流电机不仅拥有传统直流电机的优点而且取消了碳刷、滑环结构，这样的设计使其增加许多特性：无级调速、调速范围广、过载能力强、可靠性高、稳定性好、适应性强、维修与保养简单等[1]。无刷直流电机的换相逻辑电路的主要部分是控制和驱动，现在工程中经常将两者集成化为一体运用于小功率电路[2-5]。无刷直流电机简单来讲就是电机本体与驱动器的集合。永磁钢以弧形贴附在电机转子之上，位置传感器就是为了将转子的极性区分清楚。驱动器是通过接受逻辑电路的信号来控制电机换相、启动等动作，它的主要构成便是电子功率器件。采用电子换相、PWM调速既能提高BLDCM电机性能又能克服机械换向产生的一系列问题。BLDCM的转子位置是随运动系统具有时变、非线性等特点。

本文在分析无刷直流电机数学模型的基础上，采用双闭环控制系统对无刷直流电机进行仿真，实验借助了MATLAB/Simulink仿真平台验证理论分析。

2 无刷直流电机数学模型

本文以两极三相无刷直流电机为例，电机定子绕组为Y型接法，驱动电路为三相全桥电路，工作方式为两两导通(三相六状态)。简化分析过程假设：

(1) 忽略电机铁芯饱和，不计涡流磁滞损耗，不计电枢反应；

(2) 三相绕组参数相同，霍尔传感器为相差120°放置；

(3) 功率管及续流二极管为理想元件[7]。

在上述假定成立下得到无刷直流电机电压压平衡方程式：

(1)

式(1)中Ua、Ub、Uc为定子绕组相电压，Ra、Rb、Rc为相电阻，ia、ib、ic为相电流，La、Lb、Lc为绕组自感，Lab、Lac、Lba、Lbc、Lca、Lcb为绕组间互感。

其中Ra=Rb=Rc=R，

Lab=Lac=Lba=Lbc=Lca=Lcb=M。

由于三相电流满足：ia+ib+ic=0。因此式(1)可改写为：

(2)

以能量传递为基础，分析推导无刷直流电机的功率和转矩[8]。以上文的假设为前提，忽略转子的机械损耗与杂散损耗，电磁功率与动能之间不存在损耗，即电磁功率全部转化成动能[3]。其中Te为电磁转矩，Ω为电机机械角速度。即：

Pe=eaia+ebib+ecic=TeΩ

(3)

电机的运动方程为：

(4)

TL为转矩负载，J为转子转动惯量，BV为黏滞摩擦系数。

3 霍尔位置传感器-BLDCM换相逻辑

3.1 霍尔传感器信号与反电势关系

图1中ea、eb、ec描述的便是相位互差120°电角度的三相梯形波反电势其中Q1-Q6便是一个周期中的6个换相点，分别代表0°、60°、120°、180°、240°、300°。ha、hb、hc代表霍尔传感器检测转子位置时所表示的值。通过霍尔传感器的原理可以理论分析得到电机转子的位置及状态，在磁场中的根据霍尔效应，霍尔传感器会产生霍尔电压，当导体磁极大小方向变化的时候，对应的霍尔电压大小方向也将随之变动。而霍尔电压存在正负值。将正值定义为“1”，负值定义为“0”[9]。

表1阐述的是霍尔传感器信号与BLDCM驱动电路的开关管导通的关系。根据霍尔信号ha、hb、hc的逻辑关系便可对驱动电路添加触发脉冲。具体逻辑电路如图3所示。前半部分是判断霍尔传感器的信号。以转子角度在0°～60°为例，只有当ha、hb、hc的逻辑关系为101才会使AND模块输出1。此时导通驱动电路开关VT1和VT4。

图1 三相反电势与霍尔传感器信号关系

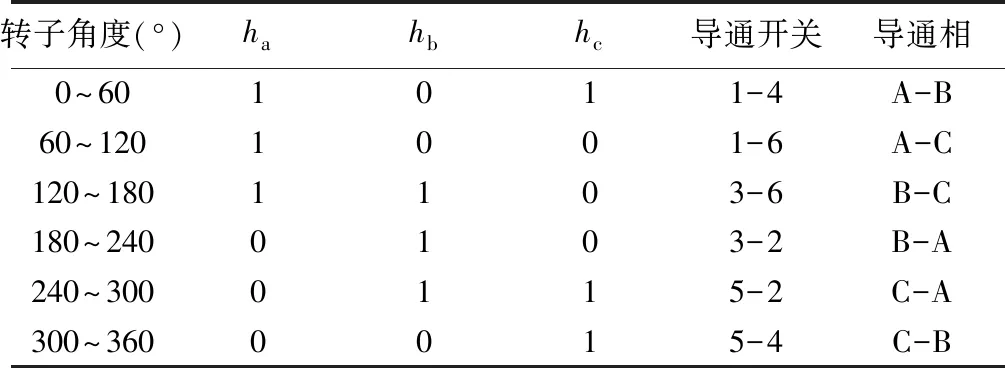
表1 逻辑换相原理

图2 BLDCM控制电路原理图

图3 触发脉冲逻辑控制电路

图4 BLDCM双闭环仿真模型

4 基于Simulink双闭环控制系统仿真模型

4.1 仿真模块

本文的无刷直流电机调速系统采用双闭环调节，内环为电流环，外环为速度环，其中速度调节器均采用PI调节控制方式。

速度调节器以转子输出转速作为输入变量，它的作用主要是有效抑制转速波动[2]。其中需要注意电机本体输出的变量为机械角速度，需要进行30/π的增益转换成转速。电流调节器的输入为定子反馈电流，它可以控制电流和转矩。

图5 BLDCM控制系统原理图

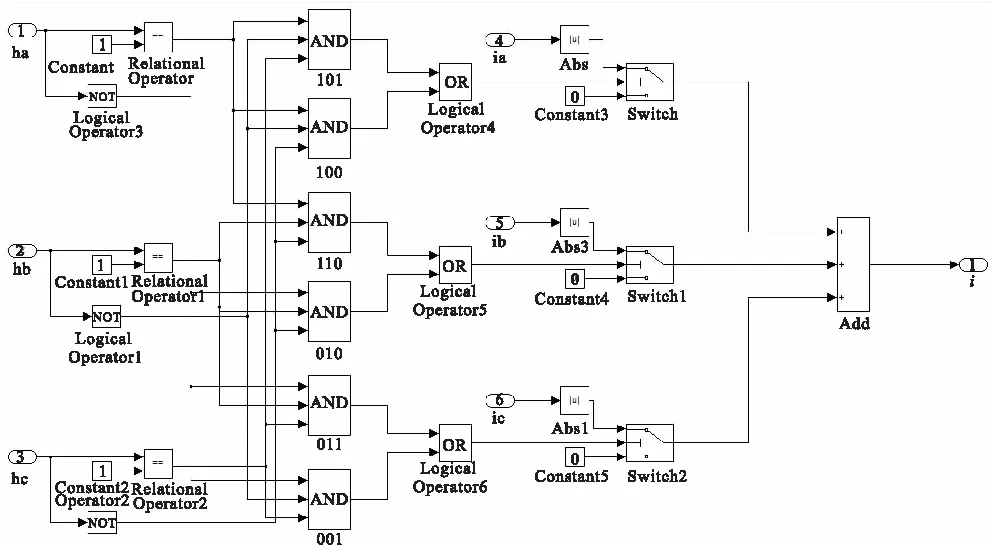
图6 电流检测控制模块

图6是电流环的电流检测控制模块，以转子角度0°～60°为例，此时只有AB项导通，即：

ia=-ib,ic=0

(5)

则只需检测ia或者ib的绝对值便可得到定子电流。

图7 BLDCM电机等效电路图

4.2 仿真结论

根据在MATALB/Simulink中建立的的双闭环仿真模型，进行无刷直流电机转速电流双闭环仿真实验。实验中，对电机负载转矩在1s时突加转矩，以此验证控制系统的静动态模型。从而得到系统相反电势、相电流、转速及电磁转矩曲线。

图8 A相反电势

图9 A相反电势(转矩突变)

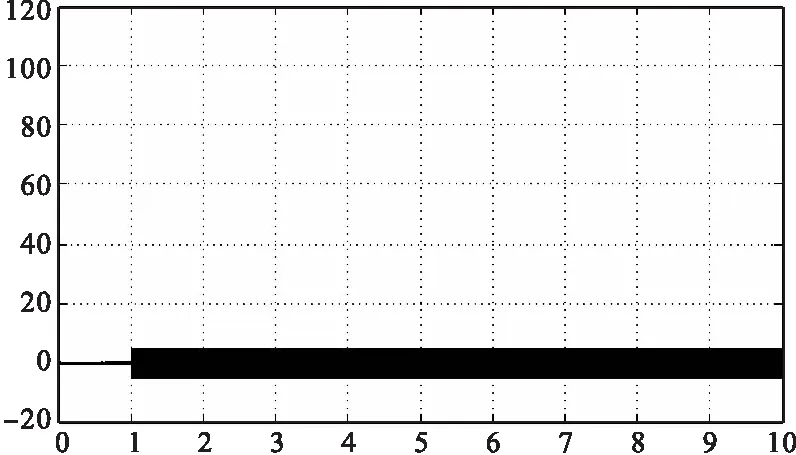
图10 A相电流

图11 A相电流(启动)

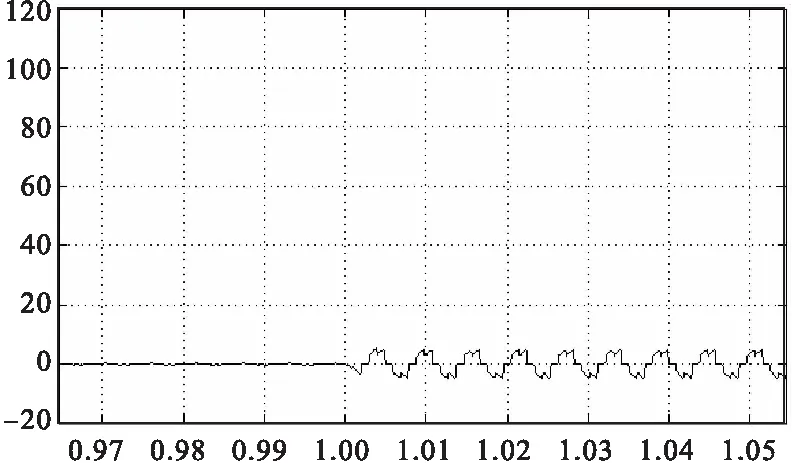
图12 A相电流(突加负载)

图13 转速

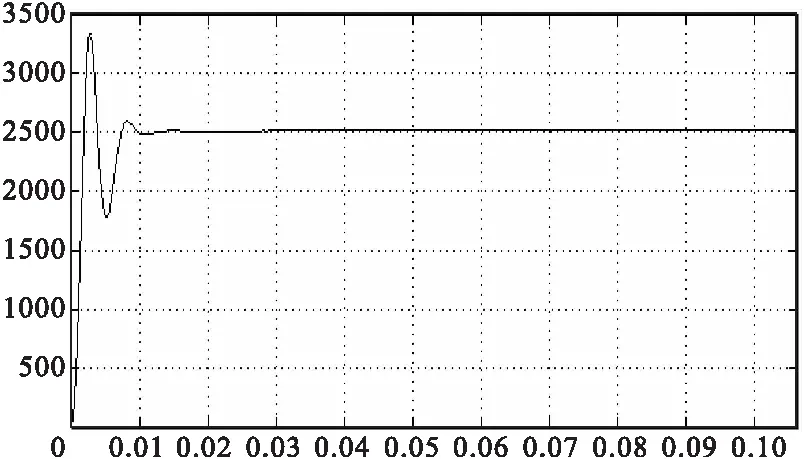
图14 转速(启动)

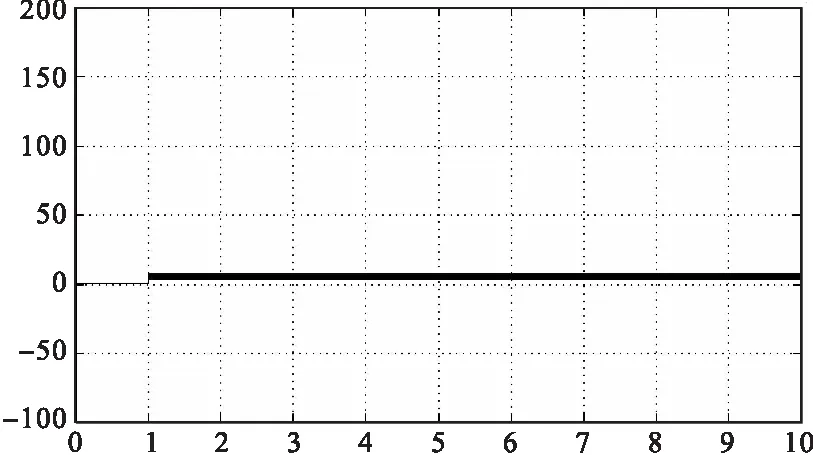
图15 电磁转矩

图16 电磁转矩(启动)

上述波形图中，每个波形第一幅图为全局，而后选取其中的启动和突加负载情况下的细化波形，在图片中均有解释。无刷直流电机的动态性能主要是对电机空载启动和突加负载转矩的暂态研究。电机空载启动，启动相电流很大，而启动稳定之后，相电流为零。假设摩擦转矩为零，此时的电磁转矩为零，波形图也明显体现出来。电机转速经过超调后进入自由加速的状态慢慢上升，相反电压波形为较理想的梯形波。在1s时突加负载转矩，此时所有参数均发生变化。但很快又进入稳定状态，在转速电流双闭环中采用PI控制环节，使得稳态时电流脉动与转矩波动不会太大。

5 结论

本文先进行无刷直流电机的数学模型推导以及霍尔传感器检测转子位置逻辑理论分析，在MATALB/Simulink的仿真下，实现对无刷直流电机双闭环PI控制系统的实验。实验结果验证了对BLDCM理论分析的正确性以及仿真模型的可靠性，对接下来省略霍尔位置传感器改为无位置传感器的无刷直流控制系统的研究提供一个前提基础。