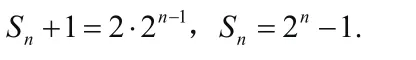数列前n项和的求法
2018-06-05
新教育时代电子杂志(教师版) 2018年9期
(辽宁省朝阳市第一高级中学 辽宁朝阳 122000)
对于等差(比)数列可利用求和公式直接求和,对于有些数列也可以用归纳法求和。此外,对于非等差(比)数列可以考虑应用以下方法求前项和。
一、分组求和法
当数列的每一项都能分成n个部分的和,并且相应部分所形成的数列是等差(比)数列时,可用此方法求解。
【例题1】已知数列满足求其前项n和
【解答】
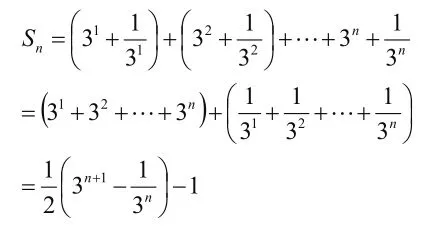
【变式1】已知数列满足 221-=+nn a ,求其前项n和

二、裂项相消法
数列的每一项都是分数,其中分子是常数,分母是若干个“间隔”相等的“连续”整数的和,此时可考虑用此方法。
【例题2】已知数列求其前项n和nS.
【解答】

【变式2】已知数列求其前项n和
【解答】
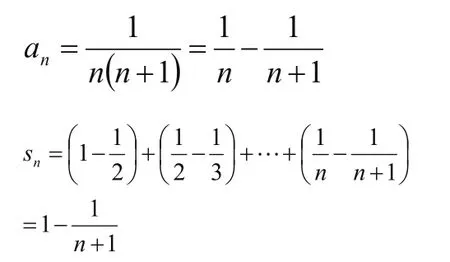
三、错位相减法
数列为等差数列,数列为等比数列,当求数列的前项n和 ns 时,可应用此法求解。
【例题3】已知数列求其前项n和
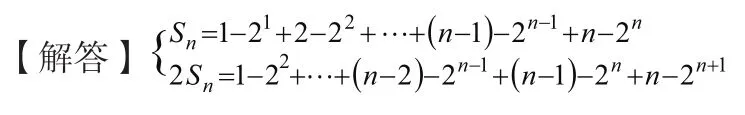
两式相减,得
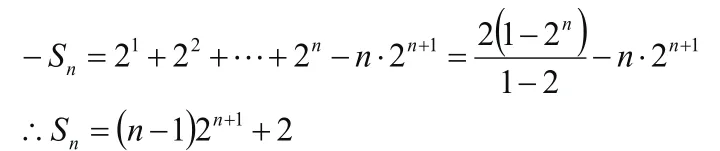
【变式3】已知数列求其前项n和
【解答】略
四、并项求和法
数列的奇数项和偶数项并在一起构成特殊数列时,可以考虑应用此法。
【例题4】数列前项n和满足
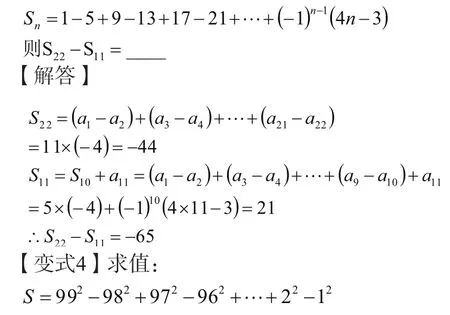
【解答】略
五、叠加法
对于一些特殊的数列(自然数的若干次方构成的数列)应用此方法较简便。
【例题5】已知数列求其前n项和
【解答】显然有

令上面式中
得n个式子,然后相加得:
应用此种方法可以求得数列的前n项和
六、通项公式 na 与其前项n和 nS的关系
【例题6】已知下面各数列的前n项和的公式。

求的通项公式
【解答】(1)当n=1时,
当2≥n时,
即
当 1=n 时,上式也成立,故通项公式为 .54-= nan
(2)当n=1时,
当2≥n时,
即
当n=1时,上式不成立,故通项公式为
七、构造法
当给出了数列的前n项和的递推关系式,可以考虑将构造成一个新数列,利用求通项的方法求出
【例题7】设数列的前n项和为且满足求数列前n项和
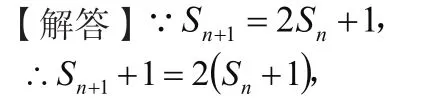
∴数列是以2为首项和公比的等比数列,故