三角翼俯仰振荡的非定常气动力降阶方法研究*

郭嘉瑞，关世玺，李立州，贾 凯，常 晶

(中北大学机电工程学院 太原 030051)

0 引言

大后掠三角翼能够减小现代飞行器在高速飞行时的气动阻力，并改善大迎角飞行的操纵性能。随着高性能计算设备与高精度计算流体力学(CFD)方法的发展，国内外对三角翼在运动状态下的非定常气动力开展了大量数值模拟研究。Gordnier等[1]数值模拟了80°三角翼的滚转运动，分析了动态流场中涡运动对非定常气动特性的影响。Ekaterinar等[2-3]数值模拟了双三角翼俯仰运动，计算得到的静止状态下物面压力分布和俯仰运动的非定常时滞力矩均与实验结果大致吻合。郭迪龙等[4]研究了俯仰滚转耦合作用对三角翼非定常气动力的影响。刘昕等[5]数值模拟了双三角翼的俯仰运动，研究了减缩频率、平均迎角和振幅对非定常气动力的影响。

三角翼大迎角下非定常流场的高精度数值模拟需要花费较多的计算资源和计算周期。因此，需要研究一种高效、高精度的降阶模型来代替CFD方法预测三角翼的非定常气动特性。Suei Chin[6]等是用Fourier变换的数学模型来预测70°三角翼大振幅俯仰运动的非定常气动力。Huang等[7]采用NIR-ISS方法，建立了大攻角下三角翼大振幅滚转运动的非定常气动力模型。史志伟等[8]采用非线性代数模型，建立了大振幅滚转运动的数学模型并提取了动导数。孙海生等[9]开展了大迎角、大振幅运动的非定常气动力建模方法的比较研究。上述建模研究成果多集中于大幅度运动时气动力宏观变化规律的预测，未涉及对小幅振荡气动力的线性与非线性分量的精确重构。

文中采用小波多分辨率分析方法对多输入Volterra核进行压缩，并预测三角翼俯仰振荡的非定常气动力。通过求解非定常Euler方程，得到了伪随机信号激励的三角翼气动力与力矩响应，辨识了76°尖前缘三角翼在两种典型迎角附近的俯仰振荡气动力与力矩。讨论了一阶、二阶Volterra核能够辨识气动响应的线性与非线性分量的能力。

1 数值模拟方法

流动控制方程采用三维非定常Euler方程，在直角坐标下的守恒积分形式为：

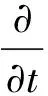
(1)

式中：Q为单位体积内质量、动量和能量组成的守恒变量；F为对流矢通量；S为边界外法向面积向量。利用有限体积法构造空间半离散格式，对流项采用二阶精度的Roe格式，时间推进采用二阶隐式LUSGS格式。动网格采用刚性旋转法，严格遵守几何守恒律[10]的要求。

2 非定常气动力降阶方法

2.1 单输入Volterra级数

对于一个多输入非线性时不变系统，对时域离散的Volterra级数可表示为如下形式：

(2)

式中：n为离散时间变量；h是系统的Volterra核；M1、M2为记忆长度。

传统的非定常气动力特点是一阶Volterra级数[11]，其向量形式为：

y(n)=h0+uTh1

(3)

为增强模型辨识非线性系统的能力，将Volterra级数扩展至二阶形式：

y(n)=h0+uTh1+uTh2u

(4)

2.2 Volterra核的小波压缩

对Volterra一阶、二阶核采用离散小波变换，得到小波域下表达形式：

一阶核：

(5)

二阶核：

(6)

式中

分别为一维与二维小波变换矩阵；W1、W2分别为一维与二维小波重构矩阵，由Mallat算法得到[12-13]：

(7)

(8)

一阶模型：

(9)

二阶模型：

(10)

式中：

2.3 自适应QR-RLS算法

采用自适应QR-RLS算法[14]辨识小波域下的Volterra核。RLS算法用卡尔曼滤波的递推公式推导出自适应滤波器权重适量更新方程，该算法具有比LMS算法更快的收敛速度，且对特征值扩展度不灵敏。其缺点是时间平均自相关矩阵的逆矩阵由于累计数值误差而失去非负定性，算法将迅速发散。为了改善RLS算法的稳定性，引入QR分解算法直接对输入矩阵进行三角分解，有效降低了自相关矩阵的条件数，提高了RLS算法的稳定性。QR-RLS算法具体步骤为：

1)k=0时，初始化矩阵U(0)：

(11)

式中δ为一个小量。

2) 对每一个k=1,2,…有：

(12)

矩阵Qθ为酉矩阵，通过连续Givens变换得到。矩阵Qθ将新的输入信号向量旋转到主对角线的上三角矩阵上。

3) 对期望输出进行连续Givens变换，得到先验误差eq1:

(13)

4) 向后迭代求解滤波器系数:

U(k)η(k)=dq2(k)

(14)

5) 计算后验误差:

(15)

式中：γ为旋转因子，λ为遗忘因子，是一个不大于1的数。

3 计算结果与分析

3.1 模型、网格与计算验证

模型为一尖前缘、76°后掠三角翼，这与文献[15]中描述的风洞模型一致，根弦长作归一化处理。网格拓补结构为O-H型，适当加密了前缘及物面法向。沿流向、周向、法向的网格点分布为81×129×44，且第一层网格距物面1×10-4倍弦长。图1给出了网格空间结构。

通过三角翼大振幅俯仰运动风洞实验验证了数值方法的非定常计算能力[15]。来流Ma数为0.3，迎角变化为α=0.024t，旋转中心为2/3根弦长处。以零迎角时的定常流场为初场，时间步长取(1×10-3) s，模拟迎角从0°～80°的俯仰运动。图2(a)、图2(b)比较了非定常升力、阻力系数的计算值和实验值。可以看出，计算程序对三角翼俯仰运动具有模拟的能力。当迎角大于40°时，计算值与实验值之间具有一定差异。这是由于迎角过大时三角翼前缘涡发生破裂，而Euler方程对涡破裂的模拟有所不足，但不失研究气动力降阶方法的可行性。

3.2 非定常气动力降阶

用上述小波压缩的Volterra核，在25°和35°迎角附近，辨识出三角翼的俯仰振荡非定常气动力。最优多层伪随机信号[16]作为输入的迎角变化信号。为提高辨识效率，对输入信号进行滤波，并使其带宽覆盖俯仰运动的减缩频率。

为验证辨识结果的准确性，通过降阶模型分别计算3°与5°幅值的俯仰振荡运动，并与CFD结果进行对比，比对的运动状态为：

状态1:α=25°+3°×sin(5t)

(16)

状态2:α=25°+5°×sin(5t)

(17)

1)25°迎角情形

从图2(a)可以看出，在25°迎角附近，三角翼俯仰运动的非定常升力系数保持较好的线性特性，因此用一阶Volterra级数辨识非定常气动力。Volterra核记忆长度为32，小波压缩后的实际辨识个数为24。图3给出了输入信号激励下的升力系数与力矩系数的CFD计算结果。图4给出了一阶Volterra核辨识结果，可以看出，Volterra核衰减得较快，而振荡幅值较弱。

图5、图6分别比较了CFD和降阶模型得到的非定常升力系数和俯仰力矩系数的时域和频域结果。可以看出，两种运动状态的非线性气动特性相对较弱。当振幅为3°时，降阶模型和CFD的计算结果在时域和频域中基本一致。当振幅增加到5°时，气动响应的非线性主频的能量略有增加。一阶Volterra级数准确地捕捉了非定常气动响应的线性主频。在峰值处两者的时域结果略有不同，是因为降阶模型无法表征非定常气动响应的非线性分量。

2)35°迎角情形

从图2(a)所示的升力系数曲线可以看出，在35°迎角附近，非定常升阻力系数开始出现明显的非线性特性。非线性气动响应分别用一阶、二阶Voltterra级数辨识。一阶核记忆长度为128，小波压缩后的实际辨识个数为96。二阶核记忆长度为32，对应的辨识参数个数为1 024，小波压缩后的实际辨识个数为576。图7给出了在输入信号激励下的升力系数与力矩系数的CFD计算结果。与25°迎角相比，升力和俯仰力矩响应的平均值更高且振幅相对较小。这表明随着迎角的增大，前缘涡吸力增加，但所产生的非线性特性抑制了气动响应的振幅。图8给出了一阶Volterra核辨识结果，可见与25°迎角相比，一阶核的收敛比较缓慢，且振荡幅值比较明显。图9,图10分别给出了升力系数和俯仰力矩系数的二阶Volterra核的辨识结果。

图11、图12比较了两种运动状态下，一阶、二阶Volterra级数与CFD计算得到的气动力时域和频域响应。可以看出，与25°迎角相比，气动响应的非线性主频能量均大幅增加。由于一阶Volterra核无法辨识出非线性分量的频率和幅值，因此一阶模型所得结果与CFD计算结果有较大差异。而二阶Volterra核能较为准确地捕捉非线性分量，辨识效果明显优于一阶模型。

4 结论

Euler方程用于数值模拟76°尖前缘三角翼的俯仰运动。利用小波压缩Volterra级数，辨识三角翼正弦振荡的非定常气动力，得出如下结论：

1) 随着平均迎角的增大，三角翼前缘涡能量和涡吸力的非线性效应显著增加。涡能量的增加增大了气动响应的均值，而涡吸力的非线性效应抑制了气动响应的振幅。

2) 一阶Volterra核具有精确的能力来辨识气动响应线性分量的频率和幅值。但无法辨识出非线性分量，对小迎角小振幅下的气动响应辨识效果较好。二阶Volterra核能较为准确的捕捉到非定常气动力和力矩的二次非线性分量，明显提高了在较大迎角和振幅下，对三角翼俯仰振荡非定常气动响应的预测能力。

3) 小波变换有助于减少一阶和二阶Volterra核的实际识别参数的个数，提高识别效率。