空气治理的有效性研究分析

吕王勇, 谢佳益, 刘小清, 余文瀚, 雷 婷, 刘安珂, 李汉堃

(1. 四川师范大学 数学与软件科学学院， 四川 成都 610066; 2. 重庆大学 数学与统计学院, 重庆 401331)

近年来，空气污染越来越成为公众关心的焦点问题.特别是2013年以来，我国中东部地区先后遭遇多次大范围持续性雾霾天气，其影响范围、持续时间、雾霾强度均为历史少见[1].据《2013中国环境状况公报》显示，2013年全国74个重点城市仅3个城市空气质量达标[2].

为了解决日渐严重的空气污染问题，我国先后颁布落实了诸多空气治理政策[3].对于环境保护而言，政策不但决定污染物的排放，而且决定节能减排的方式；对于政府而言，治理政策应对环境污染起到减速与导向作用[5].因此针对出台的诸多治理政策，评价其有效性显得尤为必要和重要.

在我国已有的针对空气治理有效性的研究中，大多都是对空气治理效果进行评价[4]，针对空气环境治理政策进行研究的课题是比较匮乏的.在这样的条件下，本文使用多维有序样本分类法对空气治理政策进行了研究.

目前，有序样本分类法已经涉及生物学[6-7]、经济学[8]、社会学[9]等领域，但是目前没有基于多维有序分类法的对大气污染的研究，故本文建立了多维有序样本分类模型，运用全局搜索法确定出最优分割点[10]，再使用假设检验模型检验最优分割下的各段是否具有显著性差异，从而证验政策的有效性.

1 研究方法

目前，广泛使用的有序分类法主要是针对大量一维的有序样本进行分类[11]，本文建立多维有序样本分类模型对有序样本分类.

假设观测对象有m个指标，其第i次观测样本为

Xi=[ai1ai2…aim],

i=1,2,…,n.

(1)

连续观测n次,得到一个n行m列的观测矩阵A，其形式如下

(2)

均值向量为

(3)

(4)

段内误差

σSSE=

(5)

段间误差

(6)

由于要使分类后得到的同一段内的对象具有很大的相似性，所以要让σSSE值尽量小；而不同段间的对象有很大的相异性，所以要让σSSA值尽量大.故定义Δ如下

(7)

寻找最优的分段个数K和每段的样本点数Jk，使得Δ最小，即

满足

(8)

1.2多元条件下的均值检验[12]根据多维有序样本分类法得到的最优分段个数N，需要判断N段均值是否存在显著差异，因此利用多总体均值的假设检验进行判断[13].假设每段样本独立同分布

… … …

(9)

提出假设：

(H0)μ1=μ2=…=μN;

(H1) 至少存在a≠b使得

μa≠μb,a,b=1,2,…,N.

检验统计量

(10)

其中

遵从维数为m，第一自由度为n-N，第二自由度为N-1的WilksΛ分布，记作

Λ～Λ(m,n-N,N-1)，

可用F分布来近似,即

F(m(N-1),ts-2λ),

(11)

其中

因此零假设的拒绝域为F>Fm(N-1),ts-2λ(α).

1.3两个正态总体均值向量的检验在完成多总体的均值检验后，若拒绝(H0)，进而需要判断每两个总体相互之间是否都具有显著性差异.

提出假设：

(H0)μa=μb；

(H1)μa≠μb(a,b=1,2,…,N).

检验统计量：

(12)

其中

因此

(13)

2 基于多维有序样本分类法的北京市空气治理有效性分析

2.1主要指标及研究地区选择根据《环境空气质量标准》[14]，最终确定可吸入颗粒物(PM10)、细颗粒物(PM2.5)、二氧化硫(SO2)、二氧化氮(NO2)、臭氧(O3)和一氧化碳(CO)作为本次研究空气质量的6个指标.本文研究的方法是一种具有推广性的一般方法，故可以运用本方法对任意城市进行空气治理有效性分析.考虑到北京是我国的政治文化中心，故选择北京作为本文的研究对象.本文在中国空气质量在线监测分析平台[15]上获得了北京市从2013年12月至2015年4月的空气质量历史数据.

2.2政策来源通过中华人民共和国环境保护部官网、北京市环境保护局官网等网站，查阅了中国环境报等相关资料，最终了解到多部法律法规涉及大气污染，如：《中华人民共和国大气污染防治法》[16]、《大气污染行动防治计划》[17]、《北京市大气污染防治条例》[18]、《2014年治理大气污染的84项工作措施》[19]、《北京市碳排放权抵消管理办法(试行)》[20]等.

2.3求解结果

2.3.1求解有序样本分类 为消除量纲及单位的影响，故将数据标准化，其中ξij为第i个样本第j个指标的值，即

j=1,2,…,6.

(14)

将标准化后的数据按公式(2)构造成515×6的观测矩阵，根据(3)～(8)式运用全局搜索法找出Δ的最小值，求解过程如图1所示.

图1 多维有序样本分类求解过程

最终搜寻到最优分类结果为：Δ最小为4.41，N=3,J1=118,J2=166,J3=231，即将样本分为3段，2个分界点日期为2014年3月28日和2014年9月10日，且各段内各指标均值如表1所示.

北京市于2014年2月14日发布了《2014年治理大气污染的84项工作措施》、于2014年9月1日发布《北京市碳排放权抵消管理办法(试行)》，可以看出，政策出台时间与分界点时间大致吻合.

表1 总体与各指标的均值

2.3.2多元条件下的均值检验 通过有序样本分类，将北京市从2013年12月至2015年4月分为3段，分界点为2014年3月28日、2014年9月10日.要使用多元条件下的均值的检验3个时间段的污染是否存在显著差异，需要检验每一段分别服从6维的正态分布，且3段相互独立.所使用的检验方法为：对每一段的6维向量分别做主成分分析，提取出6个主成分，然后分别检验6个主成分是否分别服从一维正态分布，若是，由多元正态分布的性质可知，每一段的6维向量是多元正态分布；否则，该段对应的6维向量不服从多元正态分布.经检验得到三段分别服从多元正态分布，且相互独立.使用多元条件下的均值检验，根据(9)～(11)式，验证总体差异性，均值检验结果如表2所示.

表2 多总体的均值检验

在0.05的显著性水平下，Sig.值为0，小于0.05，即拒绝(H0)∶μ1=μ2=μ3，说明分段后3个总体的均值具有显著性差异，说明政策出台前后空气质量状况有变化.

2.3.3两正态总体均值向量检验 为进一步研究段与段的均值变化情况，故根据(12)～(13)式，进一步检验两正态总体的差异性，并逐一验证两段之间各指标是否存在差异性,得到结果如表3所示.

表3 两总体的均值

由表3知，在0.05的显著性水平下，Sig.值都为0均小于0.05，即拒绝原假设μ1=μ2、μ2=μ3、μ1=μ3，说明两段之间的均值具有显著性差异.

通过表1可得，从第一段到第二段，总体均值显著性减小，说明一、二段间出台的政策使得空气质量显著提高，进而说明政策有效.从第二段到第三段，总体均值显著性升高,说明季节因素对空气质量具有影响.为排除季节因素故检验第一段与第三段的均值，结果说明在相同季节内，总体均值显著性减小，空气质量有所改善，出台政策是有效的.

通过两正态总体均值向量检验可以得出，总体的空气质量有所好转.为进一步研究各指标均值的变化情况，因此进行两总体各指标的均值检验，检验得到的显著性水平的Sig结果如表4所示.

在0.05的显著性水平下，第1段与第3段的PM10的Sig=0.40>0.05，接受原假设.但其均值从0.271 3降低为0.254 8，说明PM10减小但不显著.其余的Sig.值均小于0.05，说明从第一段到第二段，各指标均值显著性减小，即空气质量显著提高，进而说明出台的政策有效；从第二段到第三段，各指标均值显著性升高,说明季节因素对空气质量具有影响；从第一段与第三段，各指标均值来看显著性减小，说明在相同季节内空气质量有所改善，出台政策是有效的.

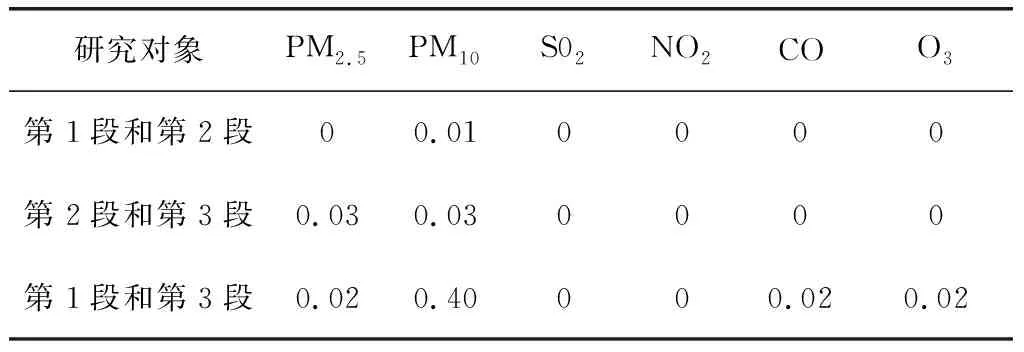
表4 两总体各指标的均值检验

3 结论

本文基于多元有序样本分类建立模型，对北京市空气质量的6种指标的数据进行研究，得出最优分割点：2014年3月28日、2014年9月10日，并使用假设检验模型检验各段均值具有显著性差异.

这一结果与现实情况吻合：北京市于2014年2月14日公布了《2014年治理大气污染的84项工作措施》，该措施发布后，3月28日到同年9月北京市空气质量有明确好转.为排除空气质量随季节、降雨量等多项自然因素影响，研究2013年冬季与2014年冬季的空气质量变化情况.北京市于2014年9月1日发布《北京市碳排放权抵消管理办法(试行)》，此管理办法从发布时间到2015年4月北京市空气质量与去年同期相比也有所好转.因此可以得出结论，《2014年治理大气污染的84项工作措施》、《北京市碳排放权抵消管理办法(试行)》对北京市空气质量的改善是有效的.由以上结论可以得知，上述2个政策对政府治理环境具有指导作用.

该结论的得出提供了一些有用的信息，有助于环境部门对下一阶段空气污染治理政策的制定，为我国治理空气污染提供一些思路和建议.

[1] 张瑾，廖宇鹏，张建忠. 雾霾天气成因分析及应对思考[J]. 中国应急管理，2014(1)：16-21.

[2] 中华人民共和国生态环境部. 2013中国环境状况公报[R/OL]. 2014-6-5. http://www.mep.gov.cn/hjzl/zghjzkgb/lnzghjzkgb/.

[3] 沈劲,钟流举,陈多宏,等. 粤东部分地区空气污染成因分析[J]. 安全与环境工程,2015(1):56-60.

[4] 何梅. 大气污染治理措施对PM10控制的有效性评价[D]. 重庆：重庆大学，2002.

[5] WANG S, XING J, ZHAO B, et al. Effectiveness of national air pollution control policies on the air quality in metropolitan areas of China[J]. J Environ Sci,2014,26(1):13-22.

[6] 张峰. 有序样本聚类在植被垂直带划分中的应用[J]. 植物生态学报,1997,21(3):267-273.

[8] 冯丽娜. 中国网络经济发展历程:基于有序样本聚类分析方法[J]. 商场现代化,2010,(14):73-73.

[9] KONIGSBERG L W. Multivariate cumulative probit for age estimation using ordinal categorical date[J]. Annals of Human Biology,2015,42(4):366-376.

[10] ZHAI Q, YANG J, ZHAO Y. Space-partition method for the variance-based sensitivity analysis:Optimal partition scheme and comparative study[J]. Reliab Engin System Safety,2014,131(3):66-82.

[11] MCCULLAGH P. Analysis of ordinal categorical data[J]. Thechnometrics,1985,27(3):317-318.

[12] 何晓群. 多元统计分析[M]. 4版. 北京:中国人民大学出版社,2015.

[13] WANG Y, MEI Y. Asymptotic Optimality Theory for Decentralized Sequential Multihypothesis Testing Problems[M]. New York:IEEE Press,2011.

[14] 中华人民共和国环境保护部. 环境空气质量标准:GB305-2012[S]. 北京:中国环境科学出版社,2012:2-29.

[15] 北京空气质量指数月统计历史数据[OL]. 中国空气质量在线监测分析平台:http://www.aqistudy.cn/.

[16] 中华人民共和国生态环境部. 中华人民共和国大气污染防治法[R/OL]. (2015-08-29). http://www.zhb.gov.cn/gzfw_13107/zcfg/fl/201605/t20160522_343394.shtml.

[17] 国务院. 大气污染行动防治计划[R/OL]. (2013-09-10). http://www.gov.cn/zwgk/2013-09/12/content_2486773.htm.

[18] 北京市环境保护局. 北京市大气污染防治条例[R/OL]. (2014-01-22). http://www.npc.gov.cn/npc/xinwen/dfrd/bj/2014-01/22/content_1824468.htm.

[19] 北京市人民政府 .2012-2020年大气污染治理措施的通知[R/OL]. (2012-3-21). http://www.bjepb.gov.cn/eportal/fileDir/oldfile/bjepb/resource/cms.

[20] 北京市环保局. 北京市碳排放权抵消管理办法(试行)[R/OL]. (2014-09-01). http://www.bjets.com.cn/article/zcfg/201407/20140700000255.shtml.