含多个非线性项的Gronwall-Bellman 型非连续函数积分不等式的推广

李自尊

(1. 四川大学 数学学院, 四川 成都 610064; 2. 百色学院 数学与统计学院, 广西 百色 533000)

积分不等式是研究微分方程和积分方程的重要工具.通过对积分不等式中未知函数的估计,可以研究某些微分方程解的存在性、唯一性、有界性和稳定性等定性性质[1-3].通过对非连续函数积分不等式中未知函数进行估计,可以研究某些脉冲微分方程解的一些性质[4-16].2007年Iovane[4]研究了非连续函数积分不等式

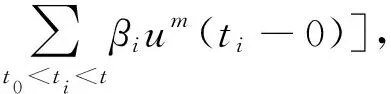
其中,a(t)>0,q(t)≥1,f(t)≥0,g(t)≥0,βi≥0.2013年严勇[5]研究了含有时滞的脉冲积分不等式

2015年米玉珍等[6]研究了含有未知函数复合的积分不等式

其中,w(u)是定义在[0,∞)上的单调不减连续函数且当u>0时,w(u)>0.

本文在上述研究的基础上，研究了一类含三项未知函数复合的非连续函数积分不等式

(*)

1 主要结果

假设

(H1)φ在[0,∞)上是严格单增的连续函数,对任意u>0,ψ(u)>0;

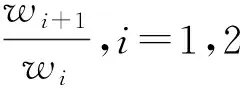
(H3)a(t)是定义在[t0,∞)上的连续函数,a(t0)≠0;

(H4)fi(t,s)(i=1,2)、f(t,s)和g(s,t)是定义在[t0,∞)×[t0,∞)上的非负连续函数;

(H5)βi≥0是常数.

∀t∈[ti,ti+1),

其中

j=2,3, ∀t∈[t0,t1),

Ei(t)=e1(t)+

βk(φ(u(ti-1))),

∀t∈[ti,ti+1),i=1,2,…,

∀t∈[ti,ti+1),i=1,2,…

j=2,3, ∀t∈[ti,ti+1).

证明令

(1)

由f(t,s)、g(t,s)和w(u(t))都是连续函数得

(2)

由(1)和(2)式,则(*)式变为

(3)

首先,考虑情况t∈[t0,t1),任意取定T∈[t0,t1),对于任意的t∈[t0,T],由(3)式得

φ(u(t))≤e1(t)+

(4)

令

则v(x)为非负不减的连续函数,且

φ(u(t))≤v(t),u(t)≤φ-1(v(t)),

v(t0)=e1(t0).

对(5)式求导可得

(6)

令

(7)

则

是不减的.由(6)和(7)式可得

(8)

从t0到t积分(8)式的两边,并利用Wi(t)的定义得到

W1(v(t))-W1(v(t0))≤

(9)

令

θ1(t)=W1(v(t)),

(10)

(11)

由(10)和(11)式,则(9)式变为

θ1(t)≤e2(t)+

令

v1(t)=e2(t)+

则v1(t)在[t0,t1)上是连续不减的函数,且θ1(t)≤v1(t),v1(t0)=e2(t0).

定义函数

i=1,2,

(13)

则

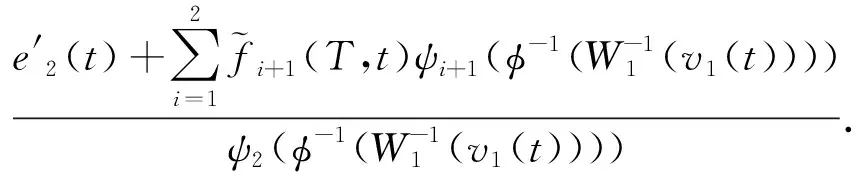
对(14)式的两边从t0到t积分,得到

(15)

由(7)、(13)和(15)式可得

Φ2(v1(t))-Φ2(v1(t0))≤

(16)

由(16)式可得

(17)

由(13)式可以推出

(18)

由(17)和(18)式可变为

(19)

令

(20)

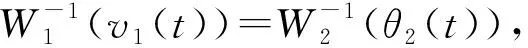
θ2(t)≤e3(t)+

令

v2(t)=e3(t)+

则v2(t)在[t0,t1)上是连续不减函数,且θ2(t)≤v2(t),v2(t0)=ρ2(t0).对v2(t)求导可得

由(23)式可得

对(24)式的两端从t0到t积分得

Φ3(v2(t))-Φ3(v2(t0))≤

则由(25)式可得

由(18)和(26)式可推出

(27)

由(5)、(10)和(20)式推出

(28)

所以可得

u(t)≤φ-1(v(t))≤

其中

由T的任意性可得

u(t)≤φ-1(v(t))≤

即当t∈[t0,t1)时证明了估计式.

当t∈[t1,t2)时,任意取T1∈[t1,t2),当t∈[t1,T1]时,不等式(3)变为

β1φ(u(t1-0))≤

β1φ(u(t1-0)).

(29)

令Γ(t)表示(29)式的右边,

E1(t)=e1(t)+

则Γ(t)是单调不减函数,且有

φ(u(t))≤Γ(t),

φ(u(t1))≤Γ(t1)=E1(t1)=

β1φ(u(t1-0)).

(30)

Γ(t)两边关于t求导得

(31)

(31)式两边同时除以w1(φ-1(Γ(t)))可得

(32)

(32)式两边从t1到t积分可得

W1(Γ(t))-W1(Γ(t1))≤

则

(33)

(33)式变为(9)式的形式,利用相同的方法可以得到估计式

∀t∈[t1,t).

同理,对任意自然数k,当t∈[tk,tk+1)时,可以得到未知函数的估计式

∀t∈[tk,tk+1).

综上定理得证.

3 在脉冲微分方程中的应用

本节用得到的结果给出脉冲微分系统解的上界估计.考虑脉冲微分系统

Δ(x)|t=ti=βix(ti-0),x(t0)=c,

(35)

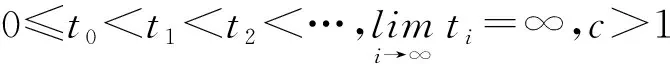
|F(t,x)|≤f(t)|xm|+

g(t)|x|ln|x|+h(t)e|x|,

(36)

其中,f(t)、g(t)和h(t)是[t0,∞)上连续的非负函数，0

推论1在条件(36)成立的情况下,系统(34)和(35)所有的解x(t)满足估计式

∀t∈[ti,ti+1),

(37)

其中

Ei(t)=c+

βk(φ(u(ti-1))),

∀t∈[ti,ti+1),i=1,2,…

j=2,3, ∀t∈[t0,t1),

∀t∈[ti,ti+1),i=1,2,…

j=2,3, ∀t∈[ti,ti+1).

(38)

证明脉冲微分方程(34)与(35)等价于积分方程

(39)

利用条件(36),由(39)式可得

(40)

令u(t)=|x(t)|,由(40)式可得不等式

(41)

令w1(u)=um,w2(u)=uln(u),w3(u)=eu,看出(41)式是(3)式的特殊形式,且(41)式中的函数满足定理1的条件.由定理1可以推出x(t)的估计式(37).

[1] AGARWAL R P, DENG S F, ZHANG W N. Generalization of a retarded Gronwall-like inequality and its applications[J]. Appl Math Comput,2005,165(3):599-612.

[2] WANG W S. A generalized retarded Gronwall-like inequality in two variables and applications to BVP[J]. Appl Math Comput,2007,191(1):144-154.

[3] 王五生,李自尊. 一类新的非线性时滞积分不等式及其应用[J]. 四川师范大学学报(自然科学版),2012,35(2):180-183.

[4] IOVANE G. Some new integral inequalities of Bellman-Bihari type with delay for discontinuous functions[J]. Nonlinear Anal,2007,66(2):498-508.

[5] 严勇. 一类带脉冲项的Gronwall-Bellman型积分不等式的推广及应用[J]. 四川师范大学学报(自然科学版),2013,36(4):603-609.

[6] 米玉珍,钟吉玉. 非连续函数的Bellman-Bihari 型积分不等式的推广[J]. 四川大学学报(自然科学版),2015,52(1):33-38.

[7] BORYSENKO S D. About asymptotical stability on linear approximation of the systems with impulse influence[J]. Ukrain Mat Zh,1983,35(2):144-150.

[8] BORYSENKO S D, CIARLETTA M, IOVANE G. Integro-sum inequalities and motion stability of systems with impulse perturbations[J]. Nonlinear Anal,2005,62(3):417-428.

[9] GALLO A, PICCIRILLO A M. About new analogies of Gronwall-Bellman-Bihari type inequalities for discontinuous functions and estimated solutions for impulsive differential systems[J]. Nonlinear Anal,2007,67(5):1550-1559.

[10] GALLO A, PICCIRILLO A M. About some new generalizations of Bellman-Bihari results for integro-functional inequalities with discontinuous functions and applications[J]. Nonlinear Anal,2009,71(12):e2276-e2287.

[11] 李自尊. 脉冲积分不等式未知函数的估计[J]. 四川师范大学学报(自然科学版),2013,36(2):258-262.

[12] 柳长青,李自尊. 一类新的非连续函数积分不等式及其应用[J]. 理论数学,2013,3(1):4-8.

[13] 孟东沅. 一类新型不连续函数的积分不等式及应用[J]. 数学的实践与认识,2009,39(2):161-166.

[14] MI Y Z, DENG S F, LI X P. Nonlinear integral inequalities with delay for discontinuous functions and their applications[J]. J Inequal Appl,2013,2013:1-11.

[15] MITROPOLSKI Y A, IOVANE G, BORYSENKO S D. About a generalization of Bellman-Bihari type inequalities for discontinuous functions and their applications[J]. Nonlinear Anal,2007,66(10):2140-2165.

[16] WANG W S, LI Z Z. A new class of impulsive integral inequalities and its application[C]//2011 International Conference on Multimedia Technology,2011,3(1):1897-1899.