基于Hoek-Brown极限平衡理论下的边坡稳定敏感性分析

魏凌傲，王正君，郜 迪

(黑龙江大学 水利电力学院，黑龙江 哈尔滨 150080)

边坡稳定是岩土工程中的一项重要内容。Mohr-Clomb准则由于其参数少，意义明确，被广泛运用于安全系数的计算，然而，Mohr-Clomb准则是一种线性的强度准则，无法体现岩土体的非线性特征，尤其是对于低应力区岩土体，误差较大。E Hoek和Brown E T在1980年[1]结合岩石性状方面的理论研究和实践经验，基于Griffith的脆性断裂理论，创造性地提出了迄今为止应用极为广泛的岩石强度准则：Hoek-Brown强度准则，可以综合考虑岩体的各方面特性。对于边坡稳定分析，结合以往的Mohr-Clomb准则以及极限平衡法，主要有瑞典法、简化Bishop法、Spencer法，以及Morgenstern-Price法。然而，对于极限平衡法结合Hoek-Brown准则的研究较少，文献[2-3]将Hoek-Brown准则与瑞典条分法、Bishop法与Morgenstern-Price法进行结合分析，但是存在计算繁琐或者不能完全体现非线性特征的缺点。同时，Hoek-Brow准则中的不同参数对岩土体的强度有较大影响，刘立鹏等[4]利用Slide软件基于Hoek-Brown准则的四个参数对岩质边坡稳定性进行分析，并定性地分析了四个参数对边坡稳定性影响的大小；李文渊[5]将Hoek-Brown准则与极限平衡理论相结合，分析了岩体不同参数对边坡安全系数的影响。但目前大量研究专注于定性比较各因素影响程度，缺乏定量对各参数影响边坡稳定性的敏感性的研究。Hoek-Brown准则中表述岩土体性质的参数具有复杂和不确定性，通过定量的敏感性分析，可以对实际工程中的边坡稳定进行指导，具有重要的实际意义。其中，灰关联度理论[6-7]作为一种成熟的敏感性分析手段被广泛地应用于边坡稳定问题中，然而运用灰关联度研究Hoek-Brown准则敏感性问题较少。

本文以某土质边坡为研究对象，介绍了Hoek-Brown准则与极限平衡法相结合的边坡稳定安全系数计算公式，通过Geo-slope软件中的Slope/w模块，基于灰关联度理论，对Hoek-Brown准则里的四个表征岩土体性质的参数进行敏感性分析，得到了各个参数对边坡稳定影响大小的定量化表述，为相应的边坡安全治理提供了参考。

1 Hoek-Brown准则与极限平衡法

2002年，E Hoek等提出了最新的H-B准则，即广义H-B经验强度准则：

(1)

式中：σ1和σ3分别为岩体破坏时的最大和最小有效主应力，kPa；σci为岩体单轴抗压强度，kPa；a为与岩体特性有关的常量；mb与s与岩体特性有关：

(2)

式中：mi为岩体性状；GSI为地质强度指标，范围为0～100;D为岩体扰动因子，范围为0～1。

s可以用下式表示：

(3)

根据式(1)可以得出σ1-σ3的值，τ-σn数据点可以这样计算：

(4)

由此可以得到τ-σn曲线，即切应力与正应力的强度包络线。

Slpoe/w可以计算每个条块底面的法向应力，即σn，由上述公式得到的强度包络线，找出曲线上该点的斜率，作为材料的内摩擦角φ，将切线延长至τ轴，截距即为黏聚力，这样，每一个条块都会有不同的c，φ值。

再由Bishop法得到滑块的安全系数，公式如下：

(5)

式中：FS为安全系数；c为土体黏聚力，kPa；β为滑块的底边长度，m;W为土条的重量，kN；α为土条底面的倾斜角，°；φ为土体的内摩擦角，°；mα可以表示为：

(6)

2 计算模型及工况

某边坡坡高为17 m，坡长为72 m，坡比为1∶1.5，地基深度取为20 m，岩体重度为25 kN/m3建立岩质边坡模型，如图1所示。

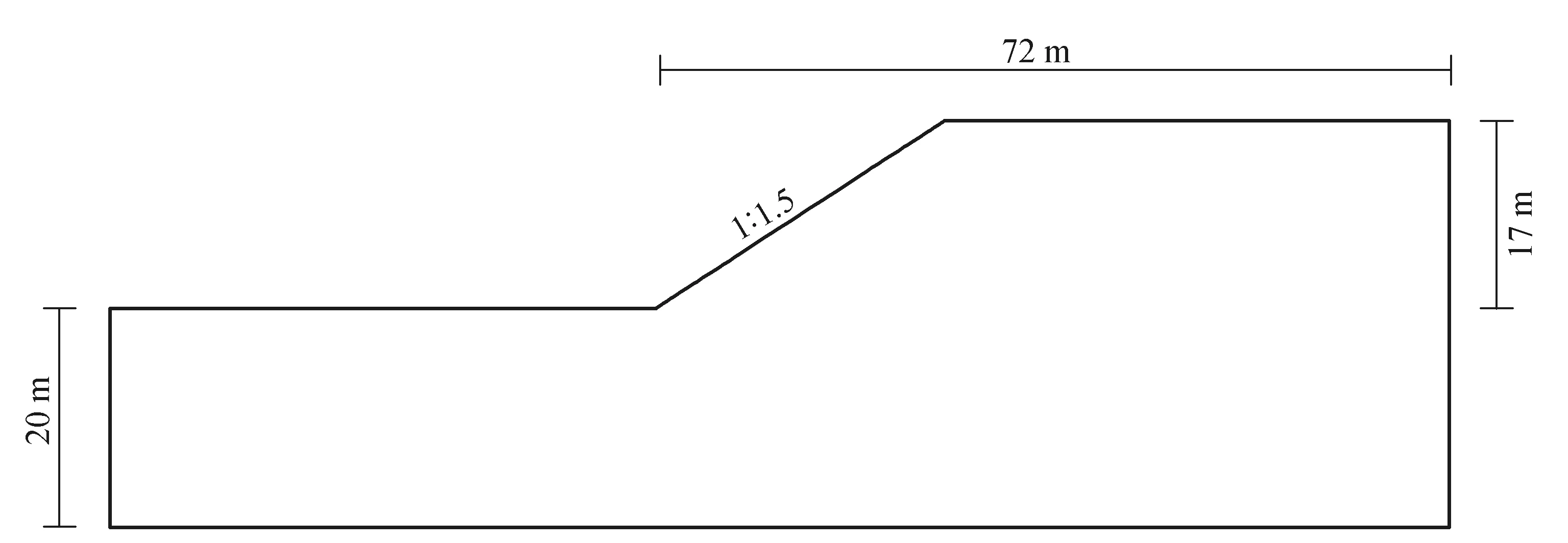
图1 计算模型

选取H-B模型四个表征岩土体性状的参数：σci，mi，GSI，D，标准参量参照文献[5]，即σci=95.0 MPa，mi=17，GSI=50，D=0.5。以此为基准，通过改变参数范围，建立以下工况,见表1。

3 边坡稳定灰关联度分析

不同工况下边坡安全系数计算结果见表2～表5。

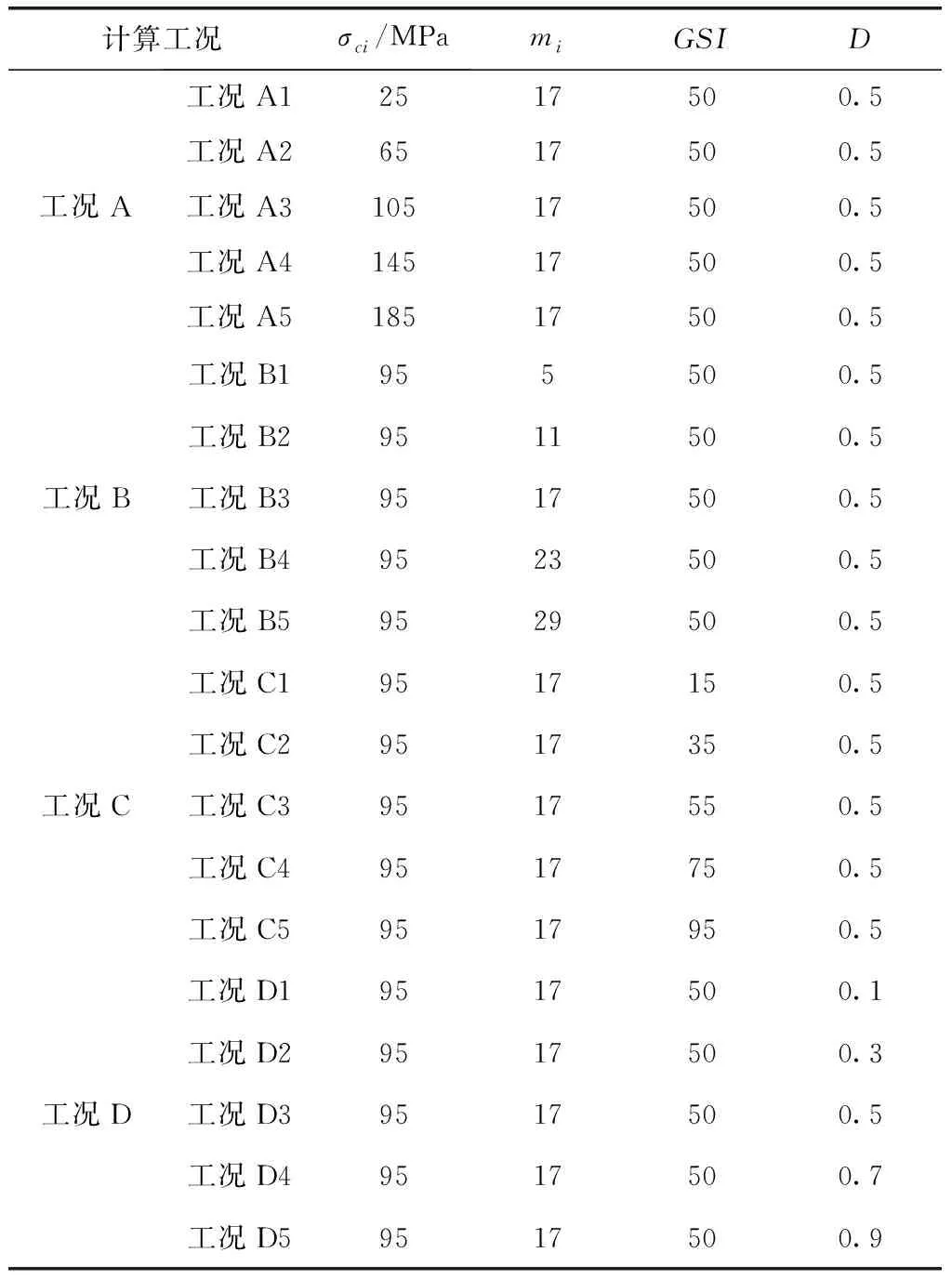
表1 计算工况

表2 工况A安全系数变化

表3 工况B安全系数变化

表4 工况C安全系数变化

表5 工况D安全系数变化

选取H-B模型中四个参数不同变化范围的变化值为比较矩阵，所对应边坡安全系数为参考矩阵，建立起比较矩阵与参考矩阵：

(8)

根据式(7)、式(8)，结合差异矩阵原始公式：

(9)

可以得到相应的差异矩阵为：

(10)

再通过灰关联系数矩阵原始公式:

(11)

式中：μ为分辨系数，范围为[0,1]，本文取为0.5。

得到其相应的灰关联系数矩阵：

(12)

于是可以求得关联度Di：Di=[0.968 0.529 0.746 0.527];得到关联度顺序为：σc i>GSI>mi>D。可见，对于H-B准则来说，影响边坡稳定性的因素中，岩体的单轴抗压强度最为敏感，其次为地质强度指标，岩体性状和岩体扰动因子对边坡影响较小，与文献[3-4]结论较为吻合，证明运用灰关联度方法分析岩质边坡稳定性是合理的。该方法计算简便，对样本数据要求较低，可以方便的从众多因素中计算出最敏感因素，为岩质边坡安全性评价提供了一种定量化的新方法。

4 结 论

本文针对于某岩质边坡，利用Geo-slope软件中的Slope/w模块，基于灰关联度理论对Hoek-Brown准则不同参数下的边坡稳定进行了敏感性分析，得出了以下结论：

(1)灰关联度理论可以将影响边坡稳定性因素定量化，直观展示各个因素的影响大小，计算简便，对样本数据要求较低，可以方便地从众多因素中计算出最敏感因素，是研究边坡稳定较为实用的方法。

(2)影响岩质边坡稳定性的最敏感的两个因素是岩体的单轴抗压强度和地质强度指标，而岩体的性状和岩体的扰动对边坡稳定性的影响较小，因此在实际边坡稳定性评估时，要通过前期勘测和现场试验准确地获取岩体相应的力学参数。

(3)灰关联度理论是单因素敏感性分析理论，本文尚未考虑各因素相互关联的情况。对于H-B准则下多因素耦合分析有待进一步研究。

(4)本文基于H-B准则对岩质边坡稳定性进行了敏感性分析，得到了岩体不同参数对边坡稳定影响大小的定量化表述，为相应的工程实际提供了参考。

[1] Eberhardt E. The Hoek-Brown Failure Criterion[J]. Rock Mechanics & Rock Engineering, 2012, 45(6):981-988.

[2] 林杭, 曹平, 李江腾,等. 基于广义Hoek-Brown准则的边坡安全系数间接解法[J]. 煤炭学报, 2008, 33(10):1147-1151.

[3] 林杭, 曹平, 李江腾,等. 基于Hoek-Brown准则的三维边坡变形稳定性分析[J]. 岩土力学, 2010, 31(11):3656-3660.

[4] 刘立鹏, 姚磊华, 陈洁,等. 基于Hoek-Brown准则的岩质边坡稳定性分析[J]. 岩石力学与工程学报, 2010, 29(S1):2879-2886.

[5] 李文渊, 吴启红. 基于Hoek-Brown非线性极限平衡法的边坡安全系数[J]. 中南大学学报(自然科学版), 2013, 44(6):2537-2542.

[6] 付建军, 邱山鸣, 赵海斌,等. 基于灰色关联度的边坡稳定影响因素分析[J]. 长江科学院院报, 2011, 28(1):53-57.

[7] 丁丽宏. 基于改进的灰关联分析和层次分析法的边坡稳定性研究[J]. 岩土力学, 2011, 32(11):3437-3441.