结合地层元素测井和密度测井提高孔隙度评价精度

袁超, 马萌, 周灿灿, 冯周, 施宇峰

(1.中国石油勘探开发研究院, 北京 100083; 2.中国石油技术开发公司, 北京 100028;3.中国石油集团测井有限公司塔里木分公司, 新疆 库尔勒 841001)

0 引 言

地层孔隙度主要采用密度测井、中子测井和声波测井等三孔隙度测井资料评价。在岩石骨架矿物简单的地层中,利用固定骨架参数值就可得到较准确的孔隙度评价结果。但是,在骨架矿物组分及含量复杂的地层中,利用三孔隙度测井及不同测井曲线交会等常规解释方法不能准确评价地层孔隙度。采用密度测井评价地层孔隙度的关键是获取取准确的骨架密度值,目前通常利用地层元素测井直接测量的元素含量反演地层矿物含量,进而计算骨架密度。地层元素测井中利用元素含量计算地层矿物含量主要有2类方法:①基于最小二乘法、广义逆矩阵法、遗传算法等最优化算法的矿物反演方法[1-2];②利用岩心的X射线衍射分析结果,建立地层矿物含量与元素含量相关性的经验公式[3-4]。但是,这些计算方法的精度都有待于进一步提高,并且利用岩心分析结果建立经验公式的方法具有很强的地区性。

本文采用基于多目标规划的最优化算法,建立适用性矿物模型和矿物系数矩阵,通过地层元素含量计算曲线与实际测井曲线不断对比,使地层矿物模型与真实地层情况吻合,可以反演计算高精度地层矿物含量。利用反演的地层矿物含量计算骨架密度,结合密度测井资料计算地层孔隙度,提高地层孔隙度的测井评价精度。

1 结合地层元素和密度测井评价孔隙度

根据岩石物理体积模型,得到密度测井响应方程[5]为

ρm·(1-φ)+ρf·φ=ρ

(1)

式中,ρm为地层骨架密度;ρf为地层流体密度;ρ为地层密度测井值;φ为地层孔隙度。

地层元素测井可以直接测量硅、钙、铁、硫、钠、镁、铝等元素含量[6-7],利用测量的地层元素含量可反演计算石英、方解石、白云石、钾长石、钠长石、伊利石、铁白云石等地层矿物含量[8]。根据反演的地层矿物含量,利用式(2)可准确的计算骨架密度

(2)

式中,n为地层骨架中所含矿物种类数;Mi为第i种地层矿物的质量百分比;ρi为第i种矿物的密度。

因此,由密度测井响应可得地层孔隙度为

(3)

2 基于多目标规划的最优化矿物反演

2.1 元素含量向矿物含量转换原理

假设地层岩石骨架中有n种矿物,每种矿物由m种元素组成,不同地层矿物中某一元素含量的总和应等于地层元素测井中测量的该元素含量,因此,满足式(4)

(4)

式中,cij为第i种矿物中第j种元素的质量百分比;Mi为第i种矿物的含量;ej为第j种元素的含量,由地层元素测井获取。

将式(4)写为矩阵形式

Cm×n·Mn×1=Em×1

(5)

式中,Cm×n、Mn×1和Em×1分别为地层矿物系数矩阵、矿物含量矩阵和元素含量矩阵。

一般情况下,地层元素测井中提供的元素含量种类m要大于反演的矿物含量种类n,因此式(4)所示的方程组为超定方程组,没有精确解,需要用最优化方法求解地层矿物含量的最优解。

2.2 基于多目标规划的矿物含量反演

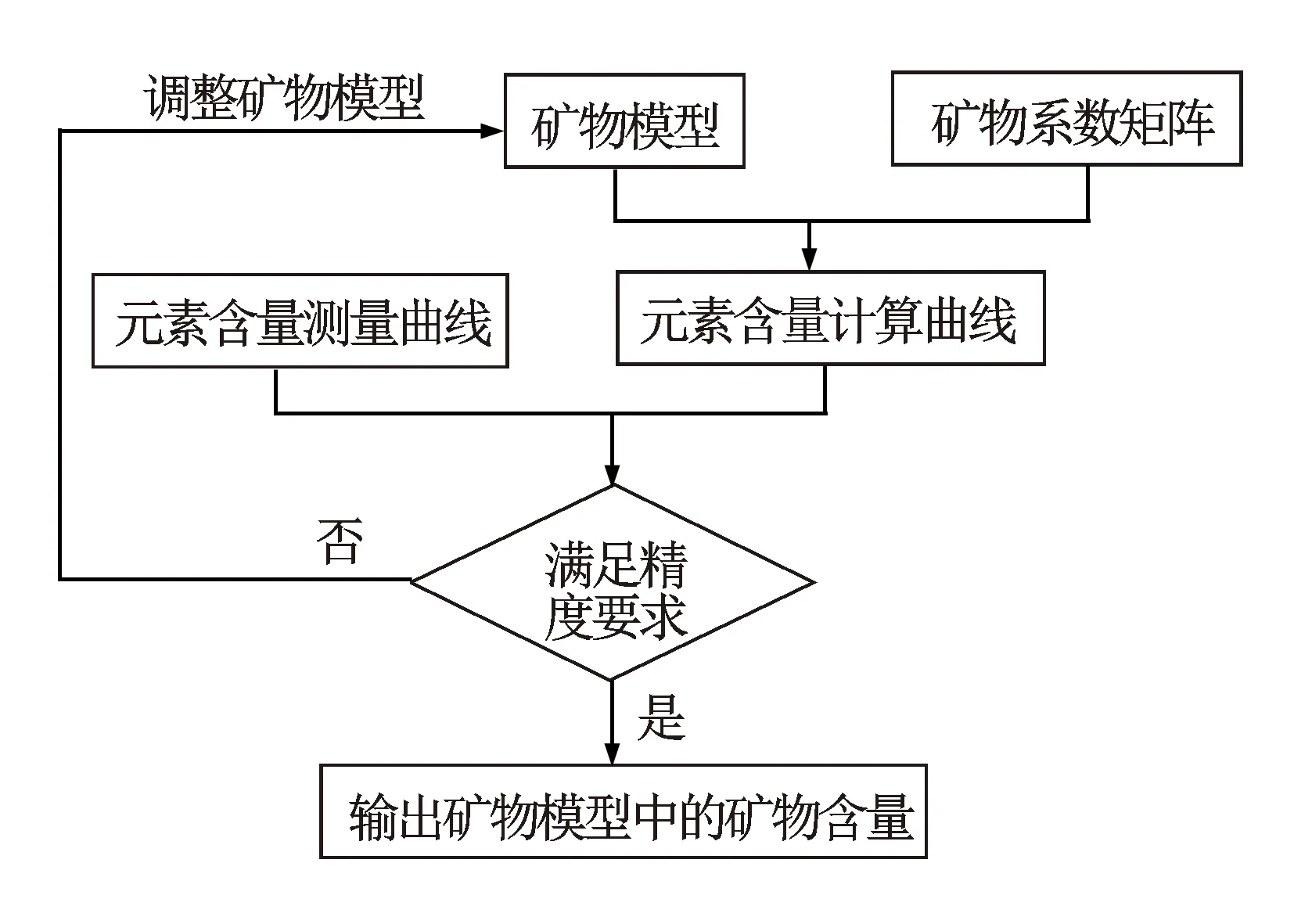
图1 多目标规划最优化矿物反演技术路线

基于多目标规划的矿物含量反演方法技术路线(见图1),根据建立的适用性矿物模型和矿物系数矩阵,计算地层元素含量曲线,不断对比地层元素含量计算曲线与实测曲线,若两者差异满足精度要求,则输出矿物模型中的矿物含量;若两者差异不满足精度要求,将其差异作为约束条件,调整地层矿物模型中的矿物含量,直至地层元素含量计算曲线与实测曲线之间的差异满足精度要求,认为此时地层矿物模型符合地层真实情况,将地层模型中的矿物含量作为最终矿物含量反演结果[9]。

地层矿物模型和矿物系数矩阵具有很强的地区性,作为矿物反演的重要输入参数,其准确性对于矿物含量反演结果的精度至关重要。对于给定的地层矿物模型,可根据不同地层矿物中的元素含量(即矿物系数矩阵)给出地层元素测井的响应曲线公式

Et=fi(v)

(6)

式中,Et为理论地层元素测井响应;fi(v)为根据给定的地层矿物模型建立的测井响应方程。

在地层矿物含量反演的最优化处理中需要求解式(5)所示的超定方程组,建立最优化目标函数

v=argmin{Fi(v)}

(7)

(8)

式中,Er为地层元素测井的元素含量测井响应;m为元素种类数。

由于不同元素含量测井曲线的不确定性不同,用于地层矿物含量反演时的可信度也不同,反演计算时对不同元素含量测井曲线采用不同权重

(9)

式中,wi为地层元素含量测井曲线的权重系数。

3 实际资料应用

×井为某油田的1口致密油井,地层矿物组分和含量比较复杂,在该井中应用斯伦贝谢公司的岩性扫描测井仪LithoScanner进行测量。根据岩心的X衍射实验分析资料,地层骨架由石英、方解石、白云石、钾长石、钠长石、伊利石、硬石膏、铁白云石等8种矿物组成,并且地层中存在干酪根。根据地层矿物组分,建立矿物含量反演中的矿物系数矩阵(见表1)。

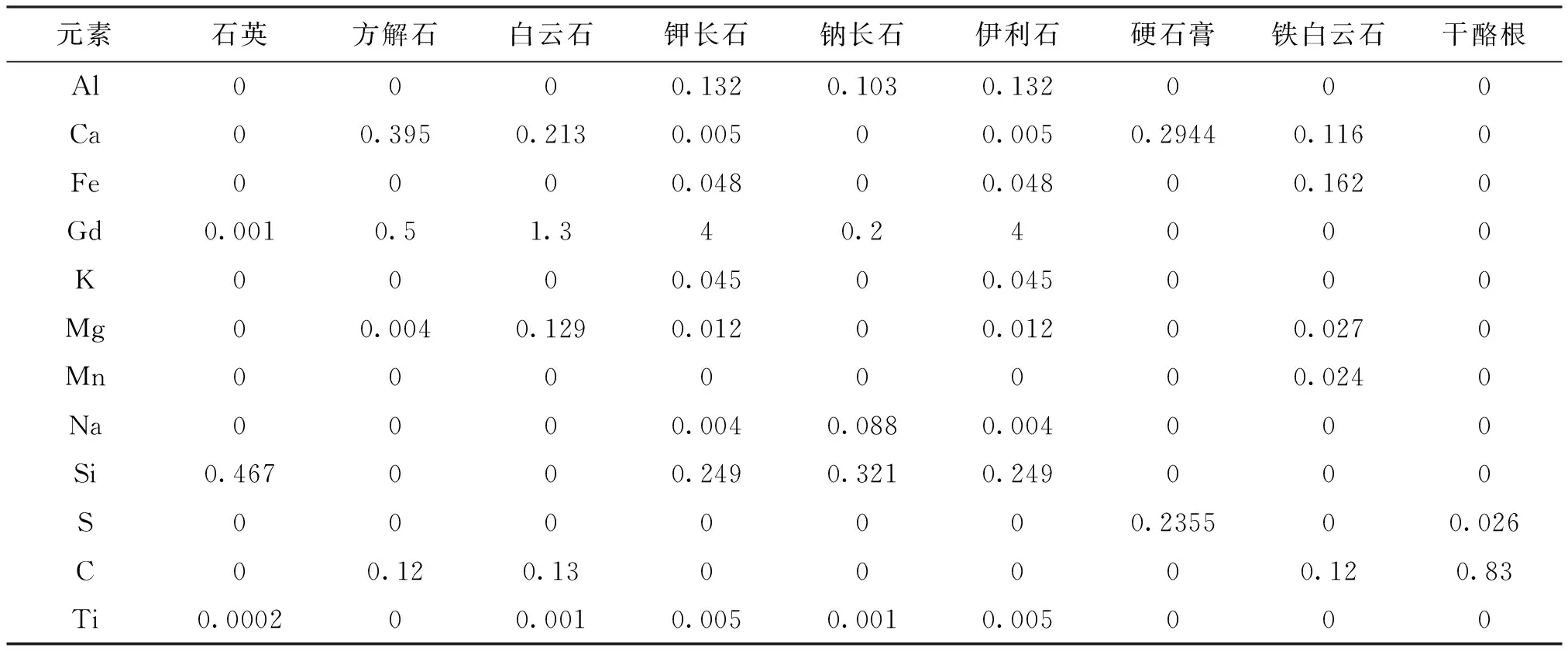
表1 ×井中地层矿物组分和含量

从图2中可以看出,密度测井计算的地层孔隙度与岩心分析结果吻合程度很差,中子—密度交会计算的孔隙度比仅利用密度测井的计算结果有一定改善,但仍与岩心分析结果有一定差异;结合地层元素和密度测井计算的地层孔隙度与岩心分析结果基本一致,比密度测井及中子—密度交会方法计算的孔隙度精度高。为进一步评价地层孔隙度计算结果,采用孔隙度计算结果与岩心分析结果的交会图以及皮尔逊相关系数。

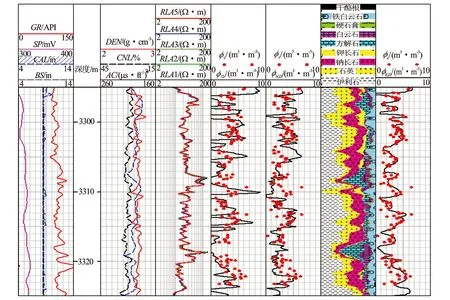
图2 ×井地层孔隙度评价成果图*非法定计量单位,1 ft=12 in=0.308 4 m,下同

如图3为地层孔隙度计算结果与岩心分析结果的交会图。图3中地层孔隙度计算结果越靠近红色对角线表明计算精度越高。根据公式(10)得到地层孔隙度计算结果与岩心分析结果的皮尔逊相关系数(见表2)。

表2 地层孔隙度计算结果与岩心分析结果的相关系数

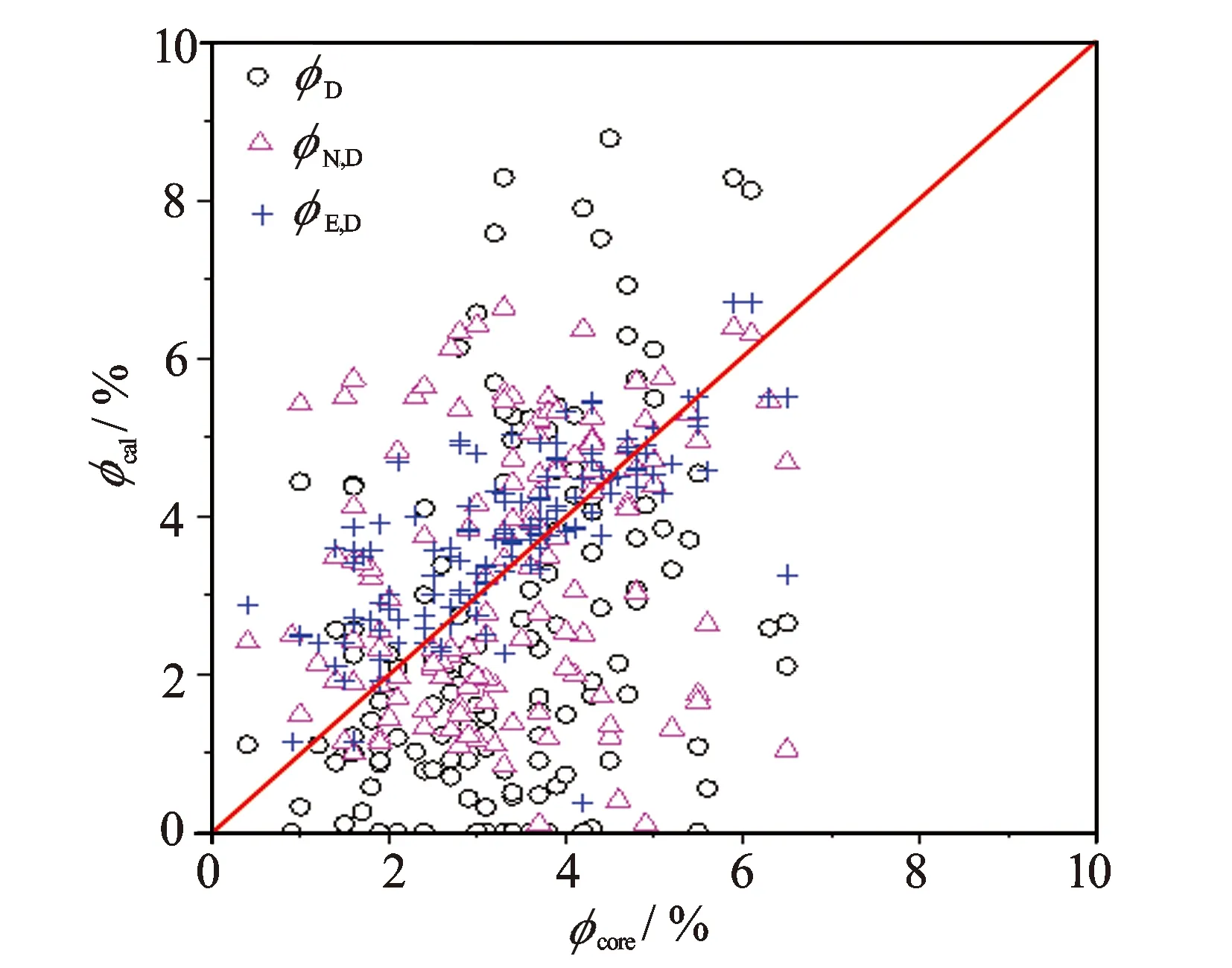
图3 ×井中地层孔隙度计算结果与岩心分析结果交会图

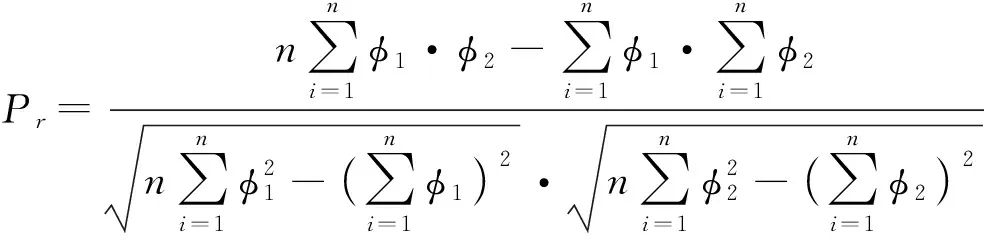
(10)

式中,φ1为地层孔隙度计算结果;φ2为地层孔隙度岩心分析结果。

如图3所示交会图及表2所示相关系数,地层元素和密度测井结合计算的地层孔隙度值基本上分布在红色对角线附近,并且其相关系数比密度测井法及中子—密度交会法的要高,证实了地层元素和密度测井结合计算地层孔隙度的精确性。

4 结 论

(1) 利用地层元素测井直接测量的元素含量反演获取地层矿物含量,进而计算岩石骨架密度,结合地层密度测井计算地层孔隙度,提高孔隙度测井评价精度。

(2) 基于多目标规划的矿物反演中,建立适用性矿物模型和矿物系数矩阵,通过不断对比地层元素计算曲线与实测曲线,使地层矿物模型与真实地层情况吻合,反演计算高精度地层矿物含量。

(3) 利用地层孔隙度计算结果与岩心分析结果的交会图以及皮尔逊相关系数验证地层孔隙度计算结果精度,结果表明地层元素和密度测井结合方法评价地层孔隙度的精度要比仅利用密度测井及中子—密度测井交会等常规解释方法的都要高。

参考文献:

[1] 孙建孟, 姜东, 尹璐. 地层元素测井确定矿物含量的新方法 [J]. 天然气工业, 2014, 34(2): 42-47.

[2] 肖佃师, 卢双舫, 陈国辉. 基于遗传算法的页岩油气储层矿物组分反演 [C]∥2014年中国地球科学联合学术年会, 北京, 2014.

[3] 章海宁, 张金功, 岳爱忠, 等. 利用地层元素识别沉积岩岩性和矿物含量计算方法 [J]. 测井技术, 2016, 40(6): 683-688.

[4] 赵军, 杨阳, 陈伟中, 等. 基于ECS测井的岩性识别方法 [J]. 地球物理学进展, 2015, 30(5): 2342-2348.

[5] 洪有密. 测井原理与综合解释 [M]. 东营: 中国石油大学出版社, 2007.

[6] GALFORD J, QUIREIN J, SCOTT S, et al. Field Test Results of a New Neutron-induced Gamma-ray Spectroscopy Geochemical Logging Tool [C]∥SPE Annual Technical Conference and Exhibition, SPE 123992, 2009.

[7] 袁超, 周灿灿. 基于伽马能谱的元素测井发展历程及技术展望 [J]. 地球物理学进展, 2014, 39(4): 1867-1862.

[8] RADTKE R J, LORENTE M, ADOLPH B, et al. A New Capture and Inelastic Spectroscopy Tool Takes Geochemical Logging to the Next Level [C]∥SPWLA 53rd Annual Logging Symposium, Paper AAA, 2012.

[9] 冯周. 复杂储层测井优化处理解释方法研究与软件实现 [D]. 北京: 中国石油勘探开发研究院, 2014.